logarytm
Lukas:
Wyznacz wszystkie wartości parametru m , dla których dziedziną funkcji
f(x) = log (mx2+4mx+m+3) jest zbiór wszystkich liczb rzeczywistych.
1. m=0
2. m>0 Δ<0
Nie trzeba jeszcze m<0 i Δ<0
28 maj 19:02
kyrtap: Df = R ⇔ ∧ mx2+4mx+m+3 > 0
x ∊R
28 maj 19:12
kyrtap: Musisz rozpatrzyć dwa przypadki kiedy funkcja jest liniowa i kwadratowa
28 maj 19:13
Lukas:
A według Ciebie −3∉R
?
28 maj 19:13
kyrtap: O co chodzi?
28 maj 19:14
Lukas:
Ja wiem o tych przypadkach, ale pytam się o 3 przypadek kiedy m<0 i Δ<0 ?
28 maj 19:14
kyrtap: Czytaj dokładnie to co napisałem
28 maj 19:14
razor: a jak wygląda taka przykładowa funkcja w której m<0 i Δ<0? narysuj i zobacz
28 maj 19:14
Lukas:
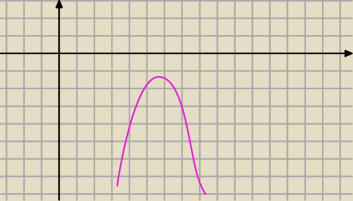
28 maj 19:15
razor: jaki wniosek? czy taka funkcja jest zawsze > 0?
28 maj 19:16
Lukas:
dobra to jest z definicji logab b>0 ?
28 maj 19:20
razor: b>0, a>0, a≠1
28 maj 19:21
Lukas:
| | log6125 | | log653 | |
a jak policzyć taki logarytm |
| ? |
| =? |
| | log65 | | log65 | |
28 maj 19:39
28 maj 19:40
razor: | | logcb | |
lub z własności logarytmu logab = |
| |
| | logca | |
| log6125 | |
| = log5125 = 3 |
| log65 | |
28 maj 19:41
Lukas:
Dzięki
28 maj 19:45
Lukas:
| | log45 | |
A takie coś |
| ? |
| | log25 | |
28 maj 20:07
28 maj 20:11
Lukas:
A skąd to ? i czemu log45 a nie log25 ?
28 maj 20:15
Mila:
Zamiana podstaw logarytmu z licznika.
28 maj 20:22
Lukas:
Nie rozumiem tego wzoru
28 maj 20:34
28 maj 20:41
Lukas:
Wiem, że jest taki wzór+robiłem zadania z tej stronki ale nie ma tam na zamiane podstawy
28 maj 20:43
Mila:
Ósmy wzór.
28 maj 20:44
Lukas:
Podstawę logarytmu wybieram jaką chcę ?
28 maj 20:46
Mila:
Jaka w danej chwili będzie Ci potrzebna. To musisz sam ustalic.
28 maj 20:47
Lukas:
a ja chciałem sobie zamienić to co mam w mianowniki a nie liczniku.. zostawię ten wzór.
28 maj 20:57
Mila:
Zamień i porównaj co się bardziej opłaca.
28 maj 20:59
Lukas:
Ok.
28 maj 21:01
Lukas:
bez sensu to wychodzi
28 maj 21:33
Mila:
| | 0,5 | | 1 | |
=log4(5)* |
| = |
| |
| | log4(5) | | 2 | |
Wg zamiany licznika:
| | 1 | |
| = |
| po skróceniu przez log2(5) |
| log25 | | 2 | |
28 maj 21:38
28 maj 21:39
kyrtap: Mila masz chwilę?
28 maj 21:40
kyrtap: sory że przeszkadzam
28 maj 21:40
Mila:
Jestem.
28 maj 21:40
28 maj 21:41
Lukas:
Nie ogarniam tego wzoru, inne zadania będę robił.
28 maj 21:42
Lukas:
wyznacz te wartości parametru m dla których funkcja f(x)=log4m+9x jest malejąca
4m+9<1 i 4m+9>0
To wystarczy ?
28 maj 22:23
kyrtap: mi się wydaje że tak
28 maj 22:25
Lukas:
Może ktoś potwierdzić ?
28 maj 22:31
kyrtap: Masz warunek <1 że jest malejąca i >0 z wł. logarytmu
28 maj 22:33
Lukas:
znam definicje, nie mam rozwiązani i pytam czy dobrze mam warunki.. kyrtap wiem że chcesz pomóc
ale czytaj co ja pisze ?
28 maj 22:34
Lukas:
Sprawdź czy funkcje są równe
f(x)=logx2 g(x)=2logx
x2>0
x∊R 2logx>0 ?
28 maj 22:56
Lukas: ?
28 maj 23:05
Mila:
No i co są równe?
28 maj 23:06
kyrtap: x2>0
D = R − {0}
28 maj 23:07
kyrtap: zastosuj pewną własność logarytmu
28 maj 23:08
Lukas:
logx2>0
x∊R\{0}
Nie są równe.
28 maj 23:22
kyrtap: a ja bym powiedział że te funkcje są równe
28 maj 23:23
razor: Funkcje nie są równe bo mają różne dziedziny
28 maj 23:24
28 maj 23:24
Mila:
f(x)=log(x
2 ) ma dziedzinę D
f=R\{0}
g(x)=2 log(x ) ma dziedzinę D
g=R
+
Funkcje nie są równe, bo mają różne dziedziny.
28 maj 23:29
jakubs: Ja wycofuje swój wpis.
Wybaczcie
28 maj 23:30
kyrtap: jeżeli mam podane funkcje tak jak Lukas podał wyżej muszę od razu wyznaczać dziedzinę bez
stosowania różnych przekształceń?
28 maj 23:31
Lukas:
Czemu pierwszego są R\{0} a w drugim R ?
28 maj 23:31
razor: tak kyrtap, podam ci przykład
log
2(−2)
2 = log
24 = 2
2log
2−2 =
28 maj 23:33
jakubs: Lukas R
+ z definicji logarytmu
https://matematykaszkolna.pl/strona/217.html
R−{0}, bo x
2>0 , a każda liczba podniesiona do kwadratu jest większa lub równa 0, więc znowu
patrzymy na definicję i wykluczamy 0 dlatego R−{0}
28 maj 23:34
Mila:
1) f(x)=log x2 liczba logarytmowana większa od zera⇔x2>0⇔x∊R\{0}
2) g(x)=log(x) liczba logarytmowana większa od zera⇔x>0 ja to zapisałam x∊R+
28 maj 23:34
kyrtap: −2
28 maj 23:34
razor: a ta własność logarytmu to nie do końca jest tak jak podają wam w tablicach, a mianowicie jest
ona spełniona tylko dla spełnionego warunku x>0. Pełna własność wygląda tak
logax2 = 2loga|x|
28 maj 23:35
kyrtap: kurde co ja piszę ...
28 maj 23:36
jakubs: Racja
razor dlatego się wycofałem z wcześniejszego wpisu
28 maj 23:36
Lukas:
Właśnie sam nie wiem co piszesz...
w drugim też powinno wyrzucić się 0 z definicji ?
28 maj 23:37
kyrtap: 2log2−2 ? nie może tam stać −2
28 maj 23:37
Lukas:
Za dużo osób.. Każdy pisze po swojemu a jak jest w końcu poprawnie ?
28 maj 23:37
Lukas:
kyrtap a możesz założyć osobny temat bo zobacz co się robi ? chciałem tutaj wstawiać swoje
zadnia.
28 maj 23:38
razor: logx2 − D: R\{0} czyli (−∞,0) ∪ (0, +∞)
2logx − D: R+ czyli (0, +∞)
28 maj 23:38
kyrtap: ok przeniosę się
28 maj 23:39
nuka:
Df = R\{0} , Dg= R+ , Df≠Dg ⇒ funkcje f i g nie są równe
28 maj 23:39
Lukas:
Wiem, że nie są równe ale czemu w pierwszym wyrzucamy 0 a w drugim nie jak mam to samo logx2
28 maj 23:40
nuka:
Najpierw masz g(x)=2*logx to D: x>0 ⇒Dg=R+
28 maj 23:44
razor: W obu wyrzucamy zero... przeczytaj jeszcze raz co ci napisała chociażby Mila
28 maj 23:45
Lukas:
2logx a to nie logx2 ta dwójka nie idzie do potęgi ?
28 maj 23:46
razor: no idzie, ale cała sprawa się rozchodzi o to że wtedy zmienia się dziedzina
28 maj 23:47
Lukas:
Nadal widzę to samo, przeczytałem to co napisała Mila.
28 maj 23:52
Lukas: ?
29 maj 00:23
Piotr:
Lukas mozesz napisac czego nie rozumiesz ? dziedziny ?
29 maj 00:27
Lukas:
Tak, dziedziny
29 maj 00:29
Piotr:
a dokladnie ktorych ? ( za bardzo namieszane w temacie jest )
29 maj 00:30
Piotr:
chodzi o funkcje :
y = log x2
y = 2logx ?
ZAWSZE patrzysz na funkcje wyjsciowa. nie ta po przeksztalceniach.
Liczba logarytmowana ma byc wieksza od 0.
w pierwszym przypadku jest tak dla kazdej liczby rzeczywistej roznej od 0.
w drugim dla kazdej wiekszej od 0.
29 maj 00:43
Lukas:
x2>0
x∊R\{0}
x>0
x∊(0,∞)
29 maj 00:44
Lukas:
Podbijam
29 maj 11:23
razor: czego nie rozumiesz? wszystko zostało już powiedziane
29 maj 11:35
Lukas:
2log(x) ?
29 maj 11:40
razor: ?
29 maj 11:41
J:
Pomimo,że logx2 = 2logx , to funkcje: y = logx2 oraz y = 2logx , mają różne dziedziny.
29 maj 11:46
Lukas:
Chodzi o wyznaczenie dziedzinu
2logx
x>0
x∊(0,∞) a podane jest, że x∊R ?
29 maj 11:47
razor: x ∊ R+ − tam jest + przy R
29 maj 11:48
razor: R+ = (0, +∞)
29 maj 11:49
J: No to jest żle podane.. y = 2logx i D = R+
29 maj 11:49
Lukas:
No właśnie.
A nie R
29 maj 11:50