geometria e: Przez wierzchołek A kąta ostrego rombu ABCD i dwa wierzchołki B i D kątów rozwartych przechodzi okrąg. dzieli on dłuższą przekątną na odcinki długości |AE|=18 3/4 i |EC|=5 1/4 Oblicz pole rombu oraz długość wysokości rombu.

kyrtap:

	183		51
|AE|=		,|EC|=
	4		4

kyrtap: Czas się zabrać za to zadanie

Lukas: ?

kyrtap: co?

Lukas: ''Czas się zabrać za to zadanie'' ? Nie wiesz jak zrobić czy co ?

kyrtap: Po prostu robiłem inne zadania i pomagałem

kyrtap: Lukas nawet jeśli nie będę wiedział to chcę pomóc

kyrtap: Mila jesteś pytanko mam czy dobrze to rozwiązane będzie?

kyrtap: Jeśli skorzystam z tw, o siecznej i stycznej?

kyrtap:

Mila: Nie wiem, czy dobrze zinterpretowałeś dane, może

	3
|AE|=18
	4

	1
|EC|=5
	4

Przez wierzchołek A kąta ostrego rombu ABCD i dwa wierzchołki B i D kątów rozwartych przechodzi

	3		1
okrąg, dzieli on dłuższą przekątną na odcinki długości |AE|=18		i |EC|=5
	4		4

Oblicz pole rombu oraz długość wysokości rombu. Mam inną koncepcję, ale oblicz a i podaj.

kyrtap: ale rysunek jest zgodny z treścią czy źle narysowany?

kyrtap:

	3√1326
Jeden z boków ma dł.
	4

kyrtap: Podobnie CI Mila wyszło czy jednak moje rozumowanie to niewypał ?

nuka: P(rombu)=216

Mila: Rysunek dobry, okrąg opisany na ΔABD. Możesz sprawdzić z tw. Pitagorasa, czy ma sens Twój wynik. ∡ADE=90 jako wpisany w okrąg oparty na średnicy. AC=24 Męcz się dalej, na pewno wymyślisz.

Mila: Nuka skąd masz ten wynik, z odpowiedzi, czy Twoich obliczeń?. Też mam taki wynik.

kyrtap: Jutro pomyślę bo już dzisiaj padam

kyrtap: Nie ma tego myślenia co przed maturą

nuka: Z moich obliczeń ......

kyrtap: ja źle zinterpretowałem dane

Mila: Hej, znam Cię niepokorna różyczko. No to nie piszemy rozwiązania. Zostawiamy to dla młodych orłów.

kyrtap: a bok jaki wam wyszedł?

Mila: Drogi Kyrtapie, więcej nie podpowiadam, może tajemnicza Różyczka Ci podpowie. Zresztą z tego co napisałyśmy możesz łatwo obliczyć.

kyrtap: ale ja chcę własnym sposobem i was zadziwić dlatego pytam

Mila: 15

nuka: a=√12²+9²= 15

pigor: hmm ... , η , a mnie wychodzi, bok rombu długości 3√14. .

Mariola : ja to zadanko jutro rano przestudiuje

nuka:

	75
|∡ADE|=90 −−− wpisany oparty na średnicy |AE|=
	4

|AC|=|AE|+|EC|=24 ⇒ |AS|=12

	21		27
|SE|=|SC|−|EC|= 12−		=
	4		4

Z trójkąta prostokątnego ABC , |DS|=x. x>0

	27
x2=|AS|*|BS| ⇒x2=12*		⇒ x=9
	4

to: |BD|=2x=18 i |AC|=24

	|AC|*|BD|
P(rombu)=		= ........ =216 [j2]
	2

W trójkącie prostokątnym ABS: |AB|=a=√|AS|²+|BS|²= √144+81= √225= 15

	P		216		72
P= a*h ⇒ h=		=		=		=14,4 [j]
	a		15		5

nuka: Ten mały trójkąt ( na rys.) ma być ADE ( sorry ....błędnie oznaczyłam

kyrtap: jej czemu ja takich rzeczy nie zauważam

pigor: ..., tak, myliłem się , bardzo ładnie η ; dobranoc .

kyrtap: ja też myliłem się pigor też mi potem tak wyszło jak Tobie

Mila: No i jest rozwiązanie.

kyrtap: jest jest ale zastanawiam czemu nie można było skorzystać z tego tw. co podałem

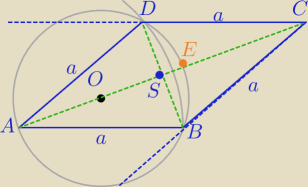
Mila: CB nie musi byc styczną do okręgu o środku O i przechodzącym przez punkty A, B i D. Narysowałam to niezupełnie w proporcjach podanych w zadaniu, aby było to widac.

kyrtap: ok dzięki Mila że tym się zainteresowałaś przeanalizuję to

pigor: ..., no właśnie a ja "uwierzyłem' w styczność tak na ... oko, stąd mój zły wynik. mam nauczkę, że ...

Eta: "na oko.... to......... padł"

kyrtap:

Eta: