świąteczne liczenie
Saizou :
zapraszam na świątyeczne liczenie
 zawodus
zawodus LO, do matury rozszerzonej, niby

19 kwi 21:33
kyrtap: a co chcesz liczyć prawdopodobieństwo namalowania stu jajek ?
19 kwi 21:35
Eta:
Liczenie ? czego? ....baranków czy zajączków?

19 kwi 21:35
Saizou : znikome szanse, dzisiaj aż jedno jajko pomalowałem i miałem dosyć xd
19 kwi 21:35
Saizou :
liczenie ? −−−−> doroczny spis
czego?−−−−−−−−> baranków, zajęcy i kurczaków
19 kwi 21:37
kyrtap: ja robię właśnie zadanie z jednokładności

19 kwi 21:38
Saizou : no to dobrze, im więcej się liczy tym potem łatwiej xd
19 kwi 21:38
zawodus: Dobrze pierwsze łatwe zadanie
 Zadanie 1
Zadanie 1
Wykazać, że dla dowolnych liczb rzeczywistych x,y,z zachodzi nierówność:
x
2+2y
2≥2(xy+x−1)
19 kwi 21:38
Eta:
Ja wciąż czekam na rozwiązanie "pewnego zadanka" ... pamiętasz? bo ja tak

19 kwi 21:39
Saizou : kojarzę coś ale nie pamiętam o co z nim chodziło...........

19 kwi 21:39
Eta:
"wykaż" ...to dla
Saizou mały pikuś

19 kwi 21:39
kyrtap: dla mnie Eta nie

19 kwi 21:41
$: wykazywanie jest najgorsze ze wszystkiego i jeszcze udowadnianie
19 kwi 21:43
kyrtap: znaczy niekoniecznie jak wiesz jak się do takich zadań zabierać
19 kwi 21:44
kyrtap: zawodus gdzie te z?
19 kwi 21:45
Saizou : to był tylko chochlik

19 kwi 21:45
kyrtap: a ja to kurde liczę
19 kwi 21:46
kyrtap: 
19 kwi 21:46
zawodus: Ukochana geometria
 Zadanie 2
Zadanie 2
Przez środek boku trójkąta równobocznego ABC poprowadzono prostą tworzącą z tym
bokiem kąt ostry α . Wyrazić stosunek pól figur na jakie ta prosta dzieli trójkąt ABC jako
funkcję kąta α.
Proszę też o nie zapominanie o pierwszym

19 kwi 21:47
kyrtap: zawodus ja nie widzę tam z?
19 kwi 21:48
zawodus: Literówka

Ale następne mogę wymyślić z "z"

19 kwi 21:49
$: te zadania to Ty z głowy wymyślasz ?
19 kwi 21:55
kyrtap: zawodus nie nic mi nie wychodzi z tym zadaniem z 1 i ja chcę zdać dobrze maturę z matmy

19 kwi 21:59
zawodus: $ po to ma się głowę, żeby z niej korzystać
 Saizou
Saizou wrzuć dowód, żeby było dla potomnych

19 kwi 22:01
kyrtap: nie wrzucaj jeszcze może coś wymyślę dajcie jeszcze 5 min
19 kwi 22:02
kyrtap: kurde poddaję się jestem ciekaw rozwiązania lipa trochę cienki ze mnie matematyk
19 kwi 22:06
Saizou :
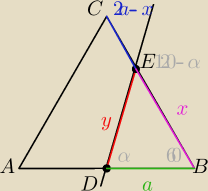
| x | | a | | asinα | |
| = |
| ⇒x= |
| |
| sinα | | sin(120−α) | | cos(30−α) | |
| | 1 | | √3 | | √3sinα | |
PBDE= |
| axsin60= |
| ax = |
| *a2 |
| | 2 | | 4 | | 4*cos(30−α) | |
| | √3sinα | |
PADEC=a2(√3− |
| ) |
| | 4*cos(30−α) | |
bardzo ładny ten stosunek

19 kwi 22:09
zawodus: Wyszedł ci straszny

19 kwi 22:10
zawodus: | | 4sin(120−α) | |
Odpowiedź to |
| −1  |
| | sinα | |
Teraz ciekawe, czy twój to to samo

19 kwi 22:11
Saizou : zaraz go uporządkuje

ale zrobię z sin(120−α) a nie z cos(30−α) xd
19 kwi 22:12
kyrtap: wrzuć te zadanie 1

19 kwi 22:14
zawodus: Saizou robisz pierwsze czy ja mam?

19 kwi 22:17
Saizou : sprawdzałem to z tymi trójkątami, na to samo wyjdzie

tylko że ja wziąłem stosunek odwrotny
xd
a tamto zadanko śmierdzi mi średnimi

19 kwi 22:20
zawodus: Saizou na maturze nie ma nierówności między średnimi

(zadanie da się zrobić bez nich
przynajmniej na dwa sposoby

19 kwi 22:21
Piotr 10: x2+2y2 − 2xy −2x+2 ≥ 0
(x − y −1)2 + y2+1 − 2y ≥ 0
(x − y −1)2 + (y−1)2 ≥ 0
c.n.w
19 kwi 22:21
Saizou : od kiedy nie ma ? wydaje mi się że można stosować wszystko co związane z matematyką, byle by
było poprawne
19 kwi 22:22
Saizou : fajnie
Piotrze, a chciałem się pogłowić

19 kwi 22:23
kyrtap: kiedy ja na taki level wbije

19 kwi 22:24
Piotr 10: zawodus mozesz sprawdzic?
19 kwi 22:25
zawodus: Można stosować, ale ich się nie uczy

Dlatego rozwiązanie musi dać się zrobić bez nich

Możesz pisać na maturze co chcesz
 Piotrek
Piotrek ok

Pytanko ile czasu zajęło ci liczenie?
19 kwi 22:27
Piotr 10: Około 7 minut , na początku chciałem to normalnie policzyć, ale później zauważyłem ze trzeba w
'wiekszy' wzor skroconego mnozenia sie zabawic

19 kwi 22:28
kyrtap: szacun
19 kwi 22:28
Piotr 10: Saizou faktycznie to zad miało byc dla Ciebie, sorry

19 kwi 22:29
zawodus: Nie trzeba "większego" wzoru wcale
 Saizou
Saizou masz okzaję pomyśleć nad łatwiejszym rozwiązaniem, a dla ciebie
kyrtap potem
podam trick na robienie wszystkich takich zadań

19 kwi 22:30
Saizou : może i dobrze że je zrobiłeś, bo ja dzisiaj kiepsko myślę trochę, bo 3 dni już walczyłem: dom
vs. ja i środki czyszczące xd
19 kwi 22:30
Piotr 10: hehe

19 kwi 22:31
Piotr 10: zawodus przecież moje rozwiązanie jest proste 2 linijki tylko

19 kwi 22:32
kyrtap: serio zawodus? byłbym wdzięczny
19 kwi 22:32
kyrtap: Piotr 10 no no

19 kwi 22:32
zawodus: Zadanie 3
Wyznacz zbiór środków cięciw paraboli y2 =3x przechodzących przez punkt P = (0, 2) .
19 kwi 22:32
Saizou : to chyba wykracza poza LO niestety

19 kwi 22:33
zawodus: Piotrek ale wzory skróconego mnożenia dla 3 składników nie są tak banalne

19 kwi 22:33
zawodus: Saizou Wcale nie

19 kwi 22:34
Piotr 10: Jak nie , wystarczy drobne podstawienie a = x − y i mamy
(a−1)2=a2 −2a+1 = (x−y)2 − 2(x−y) + 1 = x2 −2xy+y2 −2x+2y+1
19 kwi 22:34
Saizou : szczerze, pierwszy raz się spotkałem z określeniem cięciwa paraboli

19 kwi 22:36
Piotr 10: Ja miałem takie cos kiedys w arkuszu maturalnym ze szkoly o cieciwie paraboli
19 kwi 22:37
zawodus: Moja "wzorcówka" do pierwszego

(x−2y)
2+(x−2)
2≥0
x
2−4xy+4y
2+x
2−4x+4≥0
2x
2−4xy+4y
2−4x+4≥0 |:2
x
2−2xy+2y
2−2x+2≥0
x
2+2y
2≥2(xy+x−1)
c.k.d
19 kwi 22:38
zawodus: cięciwa paraboli to tak samo jak cięciwa okręgu

19 kwi 22:38
kyrtap: te y
2 ma być tak tam ?

19 kwi 22:40
Saizou :
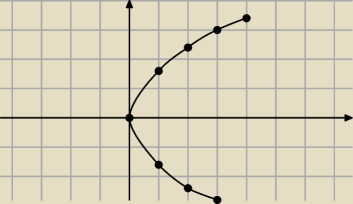
19 kwi 22:42
zawodus: Dobrze niech wam będzie zadanie
3 anulowano

19 kwi 22:49
zawodus:
zadanie 3
Rozwiąż układ równań:
x
2+y
2−4|x−y|+7=0
xy=−2

19 kwi 22:51
$: Zawodus, a jak z tym trickiem

Też bardzo chętnie się dowiem

19 kwi 22:51
Ajtek: Witam wszystkich.
Sorry za off−top, czy mamy jakiś wątek z życzeniami?
19 kwi 22:53
Marcin: zawodus co do 3, to są aż cztery rozwiązania dla x

19 kwi 22:56
kyrtap: jeju muszę tutaj z definicji wartości bezwzględnej rozwiązywać?
19 kwi 22:57
zawodus: Marcin policzyłeś?

19 kwi 22:58
razor: Wyszło mi (x,y) = (−2,1), (−1,2), (1,−2), (2,−1), dobrze jest?
19 kwi 22:58
Saizou :
(x−y)
2+2xy−4lx−yl+7=0
lx−yl
2−4lx−yl+4−1=0
(lx−yl−2)
2=1
lx−yl=3 lub lx−yl=1
i teraz easy

19 kwi 22:59
Marcin: No na szybko policzyłem, ale biorę się teraz za inne zadania

19 kwi 22:59
zawodus: Teraz rachunek
 Zadanie 4
Zadanie 4
Ze zbioru {0,1,...,9} losujemy bez zwracania 5 liczb. Oblicz prawdopodobieństwo zdarzenia
polegającego na tym, że z wylosowanych liczb można utworzyć liczbę podzielną przez 5.

19 kwi 23:04
Draghan: Powinieneś sprecyzować, w jaki sposób utworzyć

19 kwi 23:06
zawodus: Zadanie niestety nie moje, ale myślę, że chodzi o wykorzystanie wszystkich cyfr i utworzenie
liczby pięciocyfrowej

19 kwi 23:08
Draghan: Ja wiem

19 kwi 23:13
Ajtek:
zawodus zadanko banał

.
19 kwi 23:21
razor: Nie lubię prawdopodobieństwa, zawsze mam wrażenie że coś mi umyka

19 kwi 23:21
zawodus: Ajtek zadanie nie muszą być trudne

19 kwi 23:22
razor: Liczyłema na dwa sposoby i dwa razy mi wyszedł ten sam wynik więc jest jakaś szansa

P(A) =
19 kwi 23:24
kyrtap: 1/7?
19 kwi 23:27
zawodus: | | 7 | |
Odpowiedź, którą posiadam wynosi |
| |
| | 9 | |
19 kwi 23:32
zawodus: Hardcore

(bez pochodnych)
Zadanie 5
Wyznacz dziedzinę i zbiór wartości funkcji:
19 kwi 23:34
$: próbuje robić
do dziedziny mianownik>0
tylko nie mogę sprowadzić do tej samej funkcji
19 kwi 23:42
razor: to zadanie jest proste jeżeli zna się jedno fajne twierdzenie

ktoś nawet podawał je tutaj na
forum
19 kwi 23:47
ICSP: ktoś

19 kwi 23:51
19 kwi 23:58
kyrtap: zawodus będziesz miał czas jutro ?
19 kwi 23:59
zawodus: Zobaczymy

Wzór piękny, ale chyba trzeba by go udowodnić

A to może być dla was problemem

20 kwi 08:08
ICSP: To nie problem

20 kwi 12:33
20 kwi 12:35
Draghan: Zawodus, Twoja odpowiedź do zadania
czwartego jest chyba zbyt optymistyczna

Nie
sądzisz, "na zdrowy rozum", że za duże wyszło to prawdopodobieństwo?

Stawiam na wynik
razora, bo wczoraj wyliczyłem dokładnie taki sam

20 kwi 12:39
zawodus: Ja obstawiam wynik ze zbioru

20 kwi 17:18
Draghan: To ja przedstawię obliczenia, żeby nie być gołosłowny
 |Ω|
|Ω| = 9*9*8*7*6 = 27216
Rozbijam na 2 przypadki, gdzie raz ostatnią cyfrą jest zero, raz pięć.
|A| = 9*8*7*6*1 + 8*8*7*6*1 = 3024 + 2688 = 5712
| | 5712 | | 17 | |
P(A) = |
| = |
| |
| | 27216 | | 81 | |
20 kwi 17:59
razor: Tutaj pytają chyba o coś innego

Ponieważ nie losujemy kolejno, to żeby z wylosowanych cyfr
można było utworzyć liczbę podzielną przez 5 to po prostu jedną z nich musi być 0 lub 5.
A' − nie wylosowaliśmy ani 0 ani 5
|Ω| = 10*9*8*7*6
|A'| = 8*7*6*5*4
| | 8*7*6*5*4 | | 2 | |
P(A') = |
| = |
| |
| | 10*9*8*7*6 | | 9 | |
20 kwi 18:09
razor: Innymi słowy, pytanie jest o prawdopodobieństwo
możliwości utworzenia liczby podzielnej
przez 5, a nie
wylosowaniu liczby podzielnej przez 5

20 kwi 18:11
Draghan: No, chyba że dopuszczona jest taka dowolność. Wtedy owszem, zgodzę się (znów z Tobą

)

20 kwi 18:12
zawodus: Razor Dokładnie o to chodzi

20 kwi 20:16
 zawodus LO, do matury rozszerzonej, niby
zawodus LO, do matury rozszerzonej, niby 


 Zadanie 1
Wykazać, że dla dowolnych liczb rzeczywistych x,y,z zachodzi nierówność:
x2+2y2≥2(xy+x−1)
Zadanie 1
Wykazać, że dla dowolnych liczb rzeczywistych x,y,z zachodzi nierówność:
x2+2y2≥2(xy+x−1)






 Zadanie 2
Przez środek boku trójkąta równobocznego ABC poprowadzono prostą tworzącą z tym
bokiem kąt ostry α . Wyrazić stosunek pól figur na jakie ta prosta dzieli trójkąt ABC jako
funkcję kąta α.
Proszę też o nie zapominanie o pierwszym
Zadanie 2
Przez środek boku trójkąta równobocznego ABC poprowadzono prostą tworzącą z tym
bokiem kąt ostry α . Wyrazić stosunek pól figur na jakie ta prosta dzieli trójkąt ABC jako
funkcję kąta α.
Proszę też o nie zapominanie o pierwszym 
 Ale następne mogę wymyślić z "z"
Ale następne mogę wymyślić z "z" 

 Saizou wrzuć dowód, żeby było dla potomnych
Saizou wrzuć dowód, żeby było dla potomnych 





 ale zrobię z sin(120−α) a nie z cos(30−α) xd
ale zrobię z sin(120−α) a nie z cos(30−α) xd


 tylko że ja wziąłem stosunek odwrotny
xd
a tamto zadanko śmierdzi mi średnimi
tylko że ja wziąłem stosunek odwrotny
xd
a tamto zadanko śmierdzi mi średnimi 
 (zadanie da się zrobić bez nich
przynajmniej na dwa sposoby
(zadanie da się zrobić bez nich
przynajmniej na dwa sposoby 


 Dlatego rozwiązanie musi dać się zrobić bez nich
Dlatego rozwiązanie musi dać się zrobić bez nich  Możesz pisać na maturze co chcesz
Możesz pisać na maturze co chcesz  Piotrek ok
Piotrek ok  Pytanko ile czasu zajęło ci liczenie?
Pytanko ile czasu zajęło ci liczenie?


 Saizou masz okzaję pomyśleć nad łatwiejszym rozwiązaniem, a dla ciebie kyrtap potem
podam trick na robienie wszystkich takich zadań
Saizou masz okzaję pomyśleć nad łatwiejszym rozwiązaniem, a dla ciebie kyrtap potem
podam trick na robienie wszystkich takich zadań 







 (x−2y)2+(x−2)2≥0
x2−4xy+4y2+x2−4x+4≥0
2x2−4xy+4y2−4x+4≥0 |:2
x2−2xy+2y2−2x+2≥0
x2+2y2≥2(xy+x−1)
c.k.d
(x−2y)2+(x−2)2≥0
x2−4xy+4y2+x2−4x+4≥0
2x2−4xy+4y2−4x+4≥0 |:2
x2−2xy+2y2−2x+2≥0
x2+2y2≥2(xy+x−1)
c.k.d





 Też bardzo chętnie się dowiem
Też bardzo chętnie się dowiem 




 Zadanie 4
Ze zbioru {0,1,...,9} losujemy bez zwracania 5 liczb. Oblicz prawdopodobieństwo zdarzenia
polegającego na tym, że z wylosowanych liczb można utworzyć liczbę podzielną przez 5.
Zadanie 4
Ze zbioru {0,1,...,9} losujemy bez zwracania 5 liczb. Oblicz prawdopodobieństwo zdarzenia
polegającego na tym, że z wylosowanych liczb można utworzyć liczbę podzielną przez 5. 



 .
.


 P(A) =
P(A) =

 (bez pochodnych)
Zadanie 5
Wyznacz dziedzinę i zbiór wartości funkcji:
(bez pochodnych)
Zadanie 5
Wyznacz dziedzinę i zbiór wartości funkcji:
 ktoś nawet podawał je tutaj na
forum
ktoś nawet podawał je tutaj na
forum

 Wzór piękny, ale chyba trzeba by go udowodnić
Wzór piękny, ale chyba trzeba by go udowodnić  A to może być dla was problemem
A to może być dla was problemem 

 Nie
sądzisz, "na zdrowy rozum", że za duże wyszło to prawdopodobieństwo?
Nie
sądzisz, "na zdrowy rozum", że za duże wyszło to prawdopodobieństwo?  Stawiam na wynik razora, bo wczoraj wyliczyłem dokładnie taki sam
Stawiam na wynik razora, bo wczoraj wyliczyłem dokładnie taki sam 

 |Ω| = 9*9*8*7*6 = 27216
Rozbijam na 2 przypadki, gdzie raz ostatnią cyfrą jest zero, raz pięć.
|A| = 9*8*7*6*1 + 8*8*7*6*1 = 3024 + 2688 = 5712
|Ω| = 9*9*8*7*6 = 27216
Rozbijam na 2 przypadki, gdzie raz ostatnią cyfrą jest zero, raz pięć.
|A| = 9*8*7*6*1 + 8*8*7*6*1 = 3024 + 2688 = 5712
 Ponieważ nie losujemy kolejno, to żeby z wylosowanych cyfr
można było utworzyć liczbę podzielną przez 5 to po prostu jedną z nich musi być 0 lub 5.
A' − nie wylosowaliśmy ani 0 ani 5
|Ω| = 10*9*8*7*6
|A'| = 8*7*6*5*4
Ponieważ nie losujemy kolejno, to żeby z wylosowanych cyfr
można było utworzyć liczbę podzielną przez 5 to po prostu jedną z nich musi być 0 lub 5.
A' − nie wylosowaliśmy ani 0 ani 5
|Ω| = 10*9*8*7*6
|A'| = 8*7*6*5*4

 )
) 
