Wektory Anna: Prosta y=−x+3 przecina parabolę o równaniu y=x²−6x+7 w punktach A i B. Napisz równanie obrazu tej paraboli w przesunięciu o wektor WA+WB, gdzie W jest wierzchołkiem danej paraboli. Znalazłam rozwiązanie tego zadania tutaj, https://matematykaszkolna.pl/forum/166404.html Jednak czy mógłby mi ktoś wytłumaczyć czemu tam przy wektorach osoba odejmuje wektor od punktu, nie dodaje? :::( Resztę wszystko rozumiem, ale tego nie ::::(

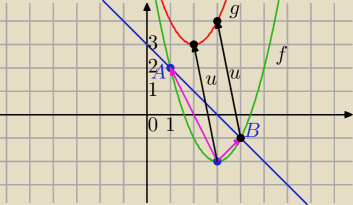
Mila: A=(1,2) B=(4,−1) x_w=3 y_w=−2 WA^→=[1−3,2−(−2)]=[−2,4] ( od wsp. końca odejmujemy wsp. początku wektora) WB^→=[4−3,−1−(−2)]=[1,1] u^→=[−2,4] +[1,1]=[−1,5] f(x)=y= x² −6x +7 po translaci o wektor [−1,5] g(x)=f(x+1)+5=(x+1)²−6*(x+1)+7+5 ⇔ g(x)=x²+2x+1−6x−6+12 g(x)=x²−4x+7

Anna: Zawsze się odejmuje? Nigdy się nie dodaje?

Mila: Współrzędne wektora? Nie masz podręcznika? https://matematykaszkolna.pl/strona/1623.html

Anna: Dziękuję

Mila: