 Przekątna graniastosłupa prawidłowego czworokątnego ma długość 18 cm i jest nachylona do
płaszczyzny podstawy pod kątem 60 stopni. Oblicz pole powierzchni oraz objętość tej bryły.
Pole powierzchni całkowitej walca wynosi 200πcm² Oblicz objętość tej bryły, jeśli wysokość jest
trzy razy większa od promienia jej podstawy.
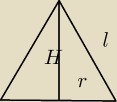
Oblicz objętość stożka, jeśli pole powierzchni bocznej wynosi 65π cm² zaś promień podstawy ma 5
cm.
Nie zależy mi na dokładnych rozwiązaniach, krok po kroku, mam to rozpisane na kartce i chce się
upewnić czy wyniki się zgadzają, pozdrawiam.
Przekątna graniastosłupa prawidłowego czworokątnego ma długość 18 cm i jest nachylona do
płaszczyzny podstawy pod kątem 60 stopni. Oblicz pole powierzchni oraz objętość tej bryły.
Pole powierzchni całkowitej walca wynosi 200πcm² Oblicz objętość tej bryły, jeśli wysokość jest
trzy razy większa od promienia jej podstawy.
Oblicz objętość stożka, jeśli pole powierzchni bocznej wynosi 65π cm² zaś promień podstawy ma 5
cm.
Nie zależy mi na dokładnych rozwiązaniach, krok po kroku, mam to rozpisane na kartce i chce się
upewnić czy wyniki się zgadzają, pozdrawiam. 
 Zadanie 3 − https://matematykaszkolna.pl/strona/1003.html
65π=π5l
l=13
H2=169−25
H=12
V=1/3π*25*12=100πcm3
Zadanie 3 − https://matematykaszkolna.pl/strona/1003.html
65π=π5l
l=13
H2=169−25
H=12
V=1/3π*25*12=100πcm3


| 729√3π | ||
V= | ||
| 2 |



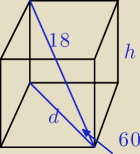
| d | ||
cos60= | ||
| 18 |
| 9√2 | ||
a= | ||
| 2 |
| H | ||
sin60= | ||
| 18 |
| 162 | 81 | |||
Pp=a2= | = | |||
| 4 | 2 |
| 81√6 | ||
Pb=a*H= | ||
| 2 |
| 162 | 81√6 | 162+81√6 | ||||
Pc=2*Pp+Pb= | + | = | ||||
| 2 | 2 | 2 |
| 81 | 729√3 | |||
V=Pp*H= | *9√3= | |||
| 2 | 2 |
| 81 | 81√6 | |||
Pc=2* | +4 | =81+162√6=81(1+2√6) | ||
| 2 | 2 |