planim bezendu: Trójkąt prostokątny ABC ma boki długości 3, 4, 5. Oblicz promień okręgu stycznego do przeciwprostokątnej i prostych będących przedłużeniami przyprostokątnych Mogę prosić rysunek ?

bezendu: ?

ja: Nakreśl poprawniej

bezendu: Dzięki ale co mi to teraz dało ?

Mila: środek okręgu stycznego do AB i przedłużeń leży na dwusiecznej kąta prostego. P punkt styczności.

ja: Prosiłeś o rys, poprowadź promienie do p styczności i masz kąty90

bezendu: Ale to nadal mi nic nie mówi ? Teraz mam jakieś 2 trójkąty prostokątne

Eta: Znasz tw. o odcinkach stycznych?

Eta: Zastosuj je w pięknym rys, jaki podała Ci Mila dla Mili

bezendu: Nie znam takiego twierdzenia ?

WAT: Zastosuj się do twierdzenia podanego przez Milo. Może pomoże Ci jeszcze fakt, iż figura CMSK jest kwadratem

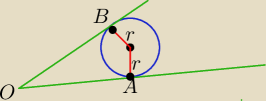
Mila: Punky styczności A i B okręgu wpisanego w kąt są jednakowo odległe od wierzchołka kąta O. OA=OB. Tam powinno być: MB=BP bo punkty styczności M i P są jednakowo odległe od wierzchołka B. AK=AP, bo punkty styczności P i K jest jednakowo odległe od wierzchołka A

bezendu: Ale akurat długości tych odcinków nie znam mam 2 nie wiadome i nic.

Eta: |PA|=x= |AK| , |PB|=y=|BM| x+y=5 x+3=4+y= R

bezendu: Takie to proste było

Mila: ? No właśnie, nie zniechęcaj się tak szybko.

bezendu: Oblicz sinusy kątów ostrych trójkąta prostokątnego, wiedząc, że stosunek długości promienia okręgu wpisanego do promienia okręgu opisanego na tym trójkącie jest równy 0 ,4 . Wyliczyłem ze stosunku

ab
	=0,2
ac+bc+c2

bezendu: Było w arkusz z R więc wydawało się trudne. Staram się nie zniechęcać ale jakoś słabo idzie .

bezendu: Nic chciałem prawie gotowca tylko chodziło mi o kontynuację mojej myśli. Ten sposób jest wgl inny od tego co ja podałem.

bezendu: Więc ponawiam pytanie jak dokończyć 23:14 ?

bezendu: A po dwa napisałaś wszystko a ja mam tylko podstawić ? A już kiedyś o tym pisałem. Ale dziękuję.

bezendu: Teraz nie mogę nic z tego wyznaczyć 0,2(ac+bc+c²)=ab ?

Eta: https://matematykaszkolna.pl/forum/241041.html już tu miałeś to zadanie ! Podałam tu jeszcze łatwiejszy sposób

Eta: Przecztaj też wpis 23:05

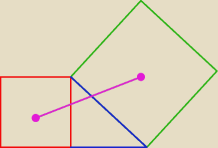
bezendu: A no miałem ale zupełnie zapomniałem. Ale tego na pewno nie robiłem: Na zewnątrz równoramiennego trójkąta prostokątnego zbudowano kwadraty – jeden na przyprostokątnej, a drugi na przeciwprostokątnej. Wykaż, że przeciwprostokątna dzieli odcinek łączący środki kwadratów na dwie równe części.

zawodus: To zadanie akurat ciekawe.

zawodus: Można przynajmniej 4 sposoby rozwiązanai podać

bezendu: ?

Mila: Po 20 . Teraz będę zajęta.

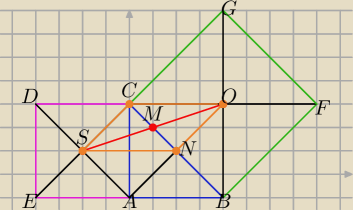
Eta: 1/jeden ze sposobów ( czworokąt SNOC −− jest równoległobokiem Opisz odpowiednim komentarzem

bezendu: Eta ale co mam opisać skoro to jest równoległobok to SN||CO oraz CS||NO i |NO|=|SC| i |CO|=|SN| ?

bezendu: Eta jesteś ?

bezendu: ?

Mila: Przekątne równoległoboku dzielą się na połowy.

bezendu: No tak i to koniec dowodu ?

Mila: Tak i Eta podała piękną wskazówkę.

bezendu: Dziękuję jeszcze takie zadanie: Suma obwodów prostokąta i trójkąta równobocznego jest równa 12. Jakie wymiary powinnien mieć prostokąt, w którym stosunek długości boków jest równy 1:2, aby suma pól tych figur była najmniejsza Moja odp: (−12+8√3)x(−24+16√3) ?

bezendu: korekta (−6+4√3)x(8√3−12)

Mila: Mój wynik: x=2(2−√3) 2x=4(2−√3) Sprawdź, jesli nie masz odpowiedzi.

bezendu: 2a+2b+3c=12

a		1
	=		⇒b=2a
b		2

2a+4a+3c=12 6a+3c=12 c=4−2a P₁=ab P₂=2a²

	c2√3
P2=		=4√3−4√3a2+√3a2
	4

P₁+P₂=(2+√3)a²−4√3a+4√3

	4√3
xa=		=−6+4√3
	2(2+√3)

b=−12+8√3 W takim razie gdzie błąd ?

Mila: Tak, zjadłam √3. x_a źle obliczyłam.Masz dobrze

bezendu: Dziękuję, w końcu jakaś nadzieja drobna.

Eta:

Eta: https://matematykaszkolna.pl/forum/243884.html tu masz hardcor

Eta: https://matematykaszkolna.pl/forum/243828.html tu coś dla Ciebie ... może być na rozszerzeniu w maju

bezendu: Mam nadzieję, że takie coś będzie jeszcze mam 40 dni.

Eta: to pod pierwszym linkiem?

bezendu: Bez przesady ! To pod drugim. I dziś ładną wskazówkę podałaś a nie wszystko zrobione i tylko dodać.. Takie coś to dla przedszkolaków

Eta: https://matematykaszkolna.pl/forum/243886.html tu zbieramy kwiatki dla Mili

bezendu: Eta żyjesz jeszcze ?

Eta: Jeszcze tak

bezendu: 10 zadań jeszcze możemy zrobić ?