24 mar 04:15
daras: czyżbyś był na korkach o 4 rano

jaka taryfa−nocna

24 mar 09:31
wredulus_pospolitus:
niestety ... złe wnioski wyciągnięte z rozwiązania
1
o m>3 (1 rozwiązanie)
2
o dlaczego tutaj masz taką samą postać po opuszczeniu modułów jak w 1
o 
m=3 (nieskończenie
wiele rozwiązań)
3
o błędnie opuszczony pierwszy moduł winno być: −(2x
2−12x+13) = m ... m∊<3,5) (2
rozwiązania), dla m=5 (1 rozwiązanie)
4
o ok ... m=3 (nieskończenie wiele rozwiązań)
5
o ok ... dla m>3 (1 rozwiązanie)
'do kupy'
− jak widzimy ... dla m<3 w żadnym przypadku nie ma ANI JEDNEGO rozwiązani

− dla m=3 mamy 'nieskończenie wiele rozwiązań' (przypadek 2
o i 3
o)
− dla m∊(3,5) mamy dokładnie 4 rozwiązania (przypadek 1
o, 2x 2
o i 5
o)
− dla m=5 mamy dokładnie 3 rozwiązania (przypadek 1
o, 2
o i 5
o)
− dla m>5 mamy dokładnie 2 rozwiązania (przypadek 1
o i 5
o)
w takim razie dla jakich 'm' mamy "wiecej niz trzy pierwiastki?"
24 mar 09:39
P@weł: To tak:
w 1o
24 mar 10:08
wredulus_pospolitus:
ale co w 1
o 
24 mar 10:19
P@weł: To tak:
w 1o:
jak widac napisalem przedzial x∊(−∞,1)
a do tego przedzialu nalezy tylko : czesc (czesc wspolna) paraboli (−∞,1) zaznaczylem kółkiem.
w 2o:
wybralem z przedziału x∊<1,2) : 1− "jedynke" , bo dwójka nie należy− jak widać przy dwójce
przedzial otwarty, podstawilem 1−dynke do modułu pierwszego |(x−2)(x−4)| = (1−2)(1−4) =
−1(−3)= 3 czyli |x|≥0 czyli modół jest dodatni i pozostał bez zmian, tak samo do modułu
drugiego podstawilem 1−dynke : |(x−1)(x−5)|= (1−1)(1−5) = 0*(−4)= 0 , wiec przedzial |x|≥0
pozostał bez zmian dlatego :
(x−2)(x−4)+(x−1)(x−5)= x2−6x+8 + x2−6x+5 = 2x2−12x+13
w 3o:
nie wiedzialem co zrobić ponieważ: mamy x∊<2,4)
podstawialem na dwa sposoby , w przedziale x∊<2,4) wybieralem 2 i 3 , bo 4 nie nalezy −
otwarty przedzial przy 4,, nooo i:
jesli podstawię 2:
|(x−2)(x−4)|= (2−2)(2−4)= 0*(−2)=0 wiec |x|≥0
jesli podstawię 3: |(x−2)(x−4)|= (3−2)(3−4)= 1*(−1) = −1 i wychodzi |x|<0 więc nie wiedzialem
czy będzie dodatnie czy ujemne.
dalej tak jak mowisz w 40 i 5o chyba poprawnie...
24 mar 10:28
wredulus_pospolitus:
2
o ... bzduuura

x∊<0,1)
więc: |−x| = .....
'podstawiam 0' ... −0 = 0 ≥ 0 ... więc |−x| ≥ 0
w takim razie |−x| = −x ... czyli m.in. −0,5 ... 'nice'
24 mar 10:32
wredulus_pospolitus:
reszta sprawy −−− nie bardzo rozumiem o co Ci chodzi teraz
24 mar 10:33
P@weł:

Nie wiem dlaczego masz dla 2
o przedzial x∊<0,1)
|(x−2)(x−4)| + |(x−1)(x−5)|
x=2 x=4 x=1 x=5 −
miejsca zerowe
patrz rysunek::
jestem nauczony zapisywac w taki sposob , po kolei wg. rysunku
(tam gdzie ukos rysunku, to otwarty)
1
o: x∊(−
∞,1)
2
o x∊<1,2)
3
o x∊<2,4)
3
o x∊<4,5)
3
o x∊<5,+
∞)
24 mar 10:42
P@weł: 4o x∊<4,5)
5o x∊<5,+∞)
błąd zapisu ,sorry
24 mar 10:44
adam: ?
24 mar 10:57
wredulus_pospolitus:
P@weł
nie zrozumiałeś mojego przesłania
piszesz że dla 2
o podstawiasz sobie x=1 ... |(x−1)(x−5)|= 0 , wiec przedzial |x|≥0 pozostał
bez zmian
co jest BZDUUUURĄ

dla x=1 i owszem |....| = 0 ≥ 0
ald już dla (np.) x = 1.5 mamy |...| = 0,5*(−4,5) = −2,25

mój przykład z 10:32 miał Ci pokazać, że NIE MOŻNA określać znaku po 'zdjęciu' podstawiając
skrajną liczbę

24 mar 11:10
adam: no racja dla 1 w :
|(x−1)(x−5)| wychodzi 0 czyli |x|≥0 a dla 1,5 w |(x−1)(x−5)| wychodzi 0,5*(−3,5)= |x|<0
24 mar 11:23
P@weł: Wredulus czyli np dla przykładu jesli mamy ten przedzial: x∊ <1,2)
i jesli pod |(x−1)(x−5)| podstawiamy skrajna liczbe 1 , i ok wychodzi 0 czyli |x|≥0
a jesli podstawiamy 1,5 pod |(x−1)(x−5)| i wychodzi −1,75 czyli |x|<0
więc jesli pojawi się choć raz |x|<0 (ujemna wartosc) to juz równanie |(x−1)(x−5)| jest:
|x|<0 czyli −(x−1)(x−5)

24 mar 11:57
ja: Ix−1IIx−5I= (x−1)(−x+5)=−(x−1)(x−5) i koniec dla x∊<1,2)
24 mar 12:20
ja: skąd Ty bierzesz zapis IxI<0
24 mar 12:21
P@weł:
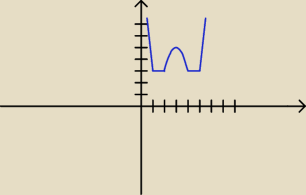
dobra , zrozumialem, poprostu nie wiedzialem ze dla 1 moze wyjsc |x|≥0 a dla 1,5 : |x|<0
1o: x∊(−
∞,1) 2x
2−12x+13
2o x∊<1,2) m=3
3o x∊<2,4) −2x
2+12x−13
3o x∊<4,5) m=3
3o x∊<5,+
∞) 2x
2−12x+13
Wszyscy klaszczą bravo


24 mar 12:27
J:
Nie podzielałbym tego entuzjazmu. Nigdy nie pisz takich bzdur, jak IxI < 0 ! IxI ≥ 0 dla
każdej liczby rzeczywistej !
24 mar 12:36
ja: A może podziękujesz jeszcze?
24 mar 12:52
wredulus_pospolitus:
Paweł −−− na przyszłość:
w 2o masz x∊<1;2)
wstawiasz x=1
|(1−1)*(1−5)| = |0*(−4)| = |0| = 0 = −0
innymi słowy ... to że dla x=0 mamy |x| = x a nie =−x to 'rzecz umowna', ale równie dobrze
można zapisać, ze:
|x| = −x dla x≤0 ⋀ |x| = x dla x>0
24 mar 13:27
P@weł: J: sorrki faktycznie nie ppomyslalem nawet o tym, wiem ze |x| : x≥0 , po prostu nie myslalem
o tym zapisując to, wiem wiem
| x≥0
|x| <|
| x<0
Bardzo , Bardzo DZIĘKUJĘ wszystkim którzy przyczynili się do pomocy

!

szczególnie wredulus za wytrwałość !
24 mar 13:45
P@weł:
|x x≥0
|x| <|
|−x x<0
24 mar 13:46
wredulus_pospolitus:
Paweł ... i jeszcze jedna sprawa (na przyszłość)
powiedz ... po co tyle przedziałów zostało wybranych

Przedziały te wybraliśmy tak, ponieważ 'pomiędzy nimi' dochodzi do jakiś 'zmian' ... więc to
powinno Ci zaświecić lampkę, że w 1
o i 2
o nie może być taka sama postać funkcji
24 mar 13:51
P@weł: Wredulus pokaż mi do których przedziałów się odnosisz bo nie wiem o czym mam mowić:
zadanie staralem się robić na zasadzie
https://matematykaszkolna.pl/strona/2545.html
Tylko ja robiłem takim schematem jakim nauczył mnie korepetytor
24 mar 14:01
P@weł:
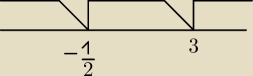
Przykładowo:
|2x−6|<|4x+2|
| | 1 | | 1 | |
przedziały 1o: x∊(−∞,− |
| ) , 2o x∊<− |
| ,3) , 3o x∊<3,+∞) |
| | 2 | | 2 | |
rozwiazywalem, szukalem czesci wspólnych i na koniec Suma części wspólnych
24 mar 14:07
ja: I prawidłowo , wcześniej należało wyłączyć 2 przed I..I
24 mar 21:39
Domel: p@weł spróbuj zrozumieć tylko mojego posta z godziny 11:43 w temacie
https://matematykaszkolna.pl/forum/242964.html
Jeżeli funkcja w nawiasach bezwzględnych |x
... + ...| jest w jakimś przedziale dodatnia to
jej znaki po opuszczeniu wartości bezwzględnej się nie zmieniają (np. dla funkcji
|x
2 − 6x + 5| w przedziałach (−oo; 1> i <5; +oo) ) czyli |x
2 − 6x + 5| = x
2 − 6x + 5
Ale jeżeli funkcja w jakimś przedziale jest ujemna (dla |x
2 − 6x + 5| w przedziale (1; 5) )
to jej znaki zmieniają się na przeciwne czyli |x
2 − 6x + 5| = −x
2 + 6x − 5
27 mar 13:02
Domel: I tak musisz rozpisać wszystkie funkcje ograniczone nawiasami wartości bezwzględnych −
określasz granice poszczególnych funkcji a potem badasz poszczególne funkcje w KAŻDEJ
WYSTĘPUJĄCEJ GRANICY. Ponieważ w twoim zadaniu miałeś 2 funkcje gdzie jedna miała granice
(−oo; 1>, (1; 5) i <5;+oo) a druga (−oo; 2>, (2; 4) i <4;+oo) to w sumie masz pięć
przedziałów:
(−oo; 1>, (1; 2>, (2; 4), <4; 5) i <5;+oo)
i DLA KAŻDEJ Z FUNKCJI MUSISZ OKREŚLIĆ ZNAKI W KAŻDYM PRZEDZIALE.
Dlatego dostaniesz 5 równań (1 równanie dla każdego przedziału)
Przedział (2; 4) jest ograniczony nawiasami otwartymi z obu stron bo WSZYSTKIE (CZYLI OBIE)
FUNKCJE W TYM PRZEDZIALE SĄ UJEMNE
27 mar 13:12
 jaka taryfa−nocna
jaka taryfa−nocna
 m=3 (nieskończenie
wiele rozwiązań)
3o błędnie opuszczony pierwszy moduł winno być: −(2x2−12x+13) = m ... m∊<3,5) (2
rozwiązania), dla m=5 (1 rozwiązanie)
4o ok ... m=3 (nieskończenie wiele rozwiązań)
5o ok ... dla m>3 (1 rozwiązanie)
'do kupy'
− jak widzimy ... dla m<3 w żadnym przypadku nie ma ANI JEDNEGO rozwiązani
m=3 (nieskończenie
wiele rozwiązań)
3o błędnie opuszczony pierwszy moduł winno być: −(2x2−12x+13) = m ... m∊<3,5) (2
rozwiązania), dla m=5 (1 rozwiązanie)
4o ok ... m=3 (nieskończenie wiele rozwiązań)
5o ok ... dla m>3 (1 rozwiązanie)
'do kupy'
− jak widzimy ... dla m<3 w żadnym przypadku nie ma ANI JEDNEGO rozwiązani  − dla m=3 mamy 'nieskończenie wiele rozwiązań' (przypadek 2o i 3o)
− dla m∊(3,5) mamy dokładnie 4 rozwiązania (przypadek 1o, 2x 2o i 5o)
− dla m=5 mamy dokładnie 3 rozwiązania (przypadek 1o, 2o i 5o)
− dla m>5 mamy dokładnie 2 rozwiązania (przypadek 1o i 5o)
w takim razie dla jakich 'm' mamy "wiecej niz trzy pierwiastki?"
− dla m=3 mamy 'nieskończenie wiele rozwiązań' (przypadek 2o i 3o)
− dla m∊(3,5) mamy dokładnie 4 rozwiązania (przypadek 1o, 2x 2o i 5o)
− dla m=5 mamy dokładnie 3 rozwiązania (przypadek 1o, 2o i 5o)
− dla m>5 mamy dokładnie 2 rozwiązania (przypadek 1o i 5o)
w takim razie dla jakich 'm' mamy "wiecej niz trzy pierwiastki?"

 x∊<0,1)
więc: |−x| = .....
'podstawiam 0' ... −0 = 0 ≥ 0 ... więc |−x| ≥ 0
w takim razie |−x| = −x ... czyli m.in. −0,5 ... 'nice'
x∊<0,1)
więc: |−x| = .....
'podstawiam 0' ... −0 = 0 ≥ 0 ... więc |−x| ≥ 0
w takim razie |−x| = −x ... czyli m.in. −0,5 ... 'nice'
 Nie wiem dlaczego masz dla 2o przedzial x∊<0,1)
|(x−2)(x−4)| + |(x−1)(x−5)|
x=2 x=4 x=1 x=5 − miejsca zerowe
patrz rysunek::
jestem nauczony zapisywac w taki sposob , po kolei wg. rysunku
(tam gdzie ukos rysunku, to otwarty)
1o: x∊(−∞,1)
2o x∊<1,2)
3o x∊<2,4)
3o x∊<4,5)
3o x∊<5,+∞)
Nie wiem dlaczego masz dla 2o przedzial x∊<0,1)
|(x−2)(x−4)| + |(x−1)(x−5)|
x=2 x=4 x=1 x=5 − miejsca zerowe
patrz rysunek::
jestem nauczony zapisywac w taki sposob , po kolei wg. rysunku
(tam gdzie ukos rysunku, to otwarty)
1o: x∊(−∞,1)
2o x∊<1,2)
3o x∊<2,4)
3o x∊<4,5)
3o x∊<5,+∞)
 dla x=1 i owszem |....| = 0 ≥ 0
ald już dla (np.) x = 1.5 mamy |...| = 0,5*(−4,5) = −2,25
dla x=1 i owszem |....| = 0 ≥ 0
ald już dla (np.) x = 1.5 mamy |...| = 0,5*(−4,5) = −2,25  mój przykład z 10:32 miał Ci pokazać, że NIE MOŻNA określać znaku po 'zdjęciu' podstawiając
skrajną liczbę
mój przykład z 10:32 miał Ci pokazać, że NIE MOŻNA określać znaku po 'zdjęciu' podstawiając
skrajną liczbę 

 dobra , zrozumialem, poprostu nie wiedzialem ze dla 1 moze wyjsc |x|≥0 a dla 1,5 : |x|<0
1o: x∊(−∞,1) 2x2−12x+13
2o x∊<1,2) m=3
3o x∊<2,4) −2x2+12x−13
3o x∊<4,5) m=3
3o x∊<5,+∞) 2x2−12x+13
Wszyscy klaszczą bravo
dobra , zrozumialem, poprostu nie wiedzialem ze dla 1 moze wyjsc |x|≥0 a dla 1,5 : |x|<0
1o: x∊(−∞,1) 2x2−12x+13
2o x∊<1,2) m=3
3o x∊<2,4) −2x2+12x−13
3o x∊<4,5) m=3
3o x∊<5,+∞) 2x2−12x+13
Wszyscy klaszczą bravo

 !
!  szczególnie wredulus za wytrwałość !
szczególnie wredulus za wytrwałość !
 Przedziały te wybraliśmy tak, ponieważ 'pomiędzy nimi' dochodzi do jakiś 'zmian' ... więc to
powinno Ci zaświecić lampkę, że w 1o i 2o nie może być taka sama postać funkcji
Przedziały te wybraliśmy tak, ponieważ 'pomiędzy nimi' dochodzi do jakiś 'zmian' ... więc to
powinno Ci zaświecić lampkę, że w 1o i 2o nie może być taka sama postać funkcji
 Przykładowo:
|2x−6|<|4x+2|
Przykładowo:
|2x−6|<|4x+2|