Funkcja Kwadratowa
P@weł: Funkcja Kwadratowa. Witam nie mam pojecia jak podejsc do tego zadania:
Dla jakich wartosci parametru m rownanie:
|x
2−6x+8| + |x
2−6x+5| = m
ma wiecej niz trzy pierwiastki?
Rozwazylem 2 opcje: 1. x≥0 i 2. x<0
1.x≥0
2x
2−12x+13=m
| | √10 | | √10 | |
x1= 3− |
| x2= 3+ |
| |
| | 2 | | 2 | |
narysowalem wykres −parabole zaznaczylem miejsca zerowe , i dalej problem bo nie wiem jaki
przedzial do tego dobrac czy :
x
2−6x+8≥0 czy x
2−6x+5≥0
czyli: x∊(−
∞,2>∪<4,
∞) x∊(−
∞,1>∪<5,
∞)
Tak bym dalej wiedzial co robic.
Tak samo : 2 opcja : x<0
−2x
2+12x−13=m
| | √10 | | √10 | |
x1= 3+ |
| x2= 3− |
| |
| | 2 | | 2 | |
zaznaczylem wierzcholek miejsca zerowe , narysowalem parabole i nie wiem dalej ktory wybrac
przedzial:
czy x
2−6x+8<0
x∊(2,4)
czy x
2−6x+5<0
x∊(1,5)
BARDZO PROSZE O PODPOWIEDZ CO ZROBIC Z TYM ZADANIEM


22 mar 10:04
wredulus_pospolitus:
zadanie mi wygląda znajomo ... sprawdziłeś czy nie było takiego przykładu tutaj w ostatnim
czasie

ale po kiego grzyba te przypadki
x≥0 i
x<0 
22 mar 10:26
wredulus_pospolitus:
Twoim zadaniem jest narysowanie f(x)=|x
2−6x+8| + |x
2−6x+5|
należy zauważyć, że: f(x) |x
2−6x+8| + |x
2−6x+5| = |(x−2)(x−4)| + |(x−1)(x−5)|
czyli:
f(x) =
| ⎧ | −(x−2)(x−4)−(x−1)(x−5); dla x<1 | |
| ⎩ | −(x−2)(x−4)+(x−1)(x−5); dla x∊<1;2) |
|
| ⎧ | (x−2)(x−4)+(x−1)(x−5)dla x∊<2;4) | |
| ⎩ | |
|
| ⎧ | −(x−2)(x−4)+(x−1)(x−5) ; dla x∊<4;5) | |
| ⎩ | −(x−2)(x−4)−(x−1)(x−5) ; dla x≥5 |
|
i rysujesz te parabole w odpowiednich przedziałach (najpierw przekształć sobie je aby wiedzieć
jak je rysować
22 mar 10:32
P@weł: Ostatnio wklejalem te same zadanie tylkko nikt tego dobrze mi nie wytlumnaczyl i dalej nie
rozumiem...
moge wiedziec skad sie wzielo tobie przedzial x<1 x∊<1,2) i dalsze przedzialy

22 mar 10:41
daras: to idź na korki

22 mar 10:54
P@weł: Wredulus ja to chcialem zrobic sposobem takim jak by sie robilo np te równanie :
|x2+3x| +1 = k
i robilem to tymi dwoma przypadkami x≥0 i x <0
22 mar 11:03
P@weł: moze mi ktos to w logiczxny sposob wytlumaczyc? bede wdzieczny,
22 mar 11:09
P@weł: moze mi ktos to w logiczxny sposob wytlumaczyc? bede wdzieczny,
22 mar 11:09
Wazyl: Paweł poczytaj o własności wartości bezwzględnej. Wredulus wyznaczył przedziały w których
zmienia się znak pod wartością.
22 mar 11:24
kika: A może tak będzie Tobie łatwiej Nakreśl w jednym układzie współrzędnych obydwie parabole
Następnie nakreśl proste y=m i popatrz gdzie masz trzy punkty wspólne z parabolami
Wredulus Tobie rozpisał na postać iloczynową , postaraj się zrozumieć na spokojnie , bez emocji
negatywnych.
22 mar 11:28
P@weł: kurcze, rozumiem wlasnosci wartosci bezwzglednej , gduby tu byla 1 wartosc bezwzgledna to to
bylo by mi latwiejsze rozpisuje 2 przypadki x≥0 i x<0 i sprawdzam przedzial i wszystko
wychodzi a tu jakos z dwiema mi sie pogmatwalo...
22 mar 11:32
kika: Nie ucz się schematami.
Rozpisz Ix2−6x+8I
22 mar 11:36
Domel:
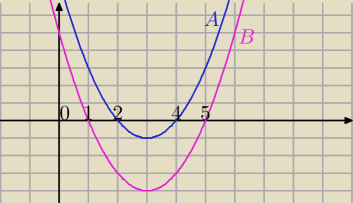
A − y = x
2 − 6x + 8
B − y = x
2 − 6x + 5
Widzisz już skąd wzięły się przedziały


No i masz:
x∊(−oo; 1) => |x
2 − 6x + 8| = x
2 − 6x + 8 − bo funkcja jest dodatnia w tym przedziale
|x
2 − 6x + 5| = x
2 − 6x + 5 − j.w.
x∊(1; 2) => |x
2 − 6x + 8| = x
2 − 6x + 8 − bo funkcja jest dodatnia w tym przedziale
|x
2 − 6x + 5| = −x
2 + 6x − 5 − bo funkcja jest ujemna w tym przedziale.
Kolejne przedziały sprawdź sam a potem masz układ równań jak podał ci
wreduluspospolitus
22 mar 11:43
Domel: wreduluspospolitus czy w przedziale (1; 2) nie zamieniłeś funkcji?
A u mnie przedział (−oo, 1) powinien wyglądać (−oo; 1>
22 mar 11:46
Domel: No i przedział (1; 2) powinien wyglądać (1; 2> − sorki za bagałan

22 mar 11:50
P@weł: Domel , dalej odbijam to co jest pod x−em nad x bo jest wartosc bezwzgledna |x| co?
22 mar 11:50
Domel: Popatrz − w przedziale (−oo; 1> obie funkcje są ≥ 0 czyli ich suma będzie ≥ 0 (więc nad osią
„x")
W przedziale (1; 2> jedna funkcja jest ≥ 0 (więc nie zmieniamy jej znaku) a druga < 0
(zmieniamy znaki w funkcji na przeciwne − i uzyskujemy wartości ≥ 0) − no i suma tych funkcji
znowu będzie ≥ 0.
Dalej analogicznie − jak zauważyłeś − zawsze funkcje dostaniemy ≥ 0 więc wartości ich sumy też
będą ≥ 0
22 mar 11:57
P@weł: Sorry za kłopot poprostu chcialem zrobic w taki sposób
http://www.zadania.info/512834
tu wyznaczalem przedzialy , rozwazylem 2 opcje x≥0 i x<0 i wszystko wychodzilo
22 mar 12:06
Domel:
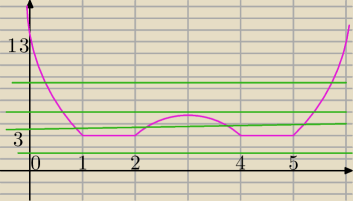
Tak mniej więcej wygląda wykres twojej funkcji (fioletowe linie) a zielone linie to potencjalne
wartości „m” (y = m) − no i gdzie jest więcej niż 3 przecięcia?
22 mar 12:21
24 mar 09:40


 ale po kiego grzyba te przypadki x≥0 i x<0
ale po kiego grzyba te przypadki x≥0 i x<0 


 A − y = x2 − 6x + 8
B − y = x2 − 6x + 5
Widzisz już skąd wzięły się przedziały
A − y = x2 − 6x + 8
B − y = x2 − 6x + 5
Widzisz już skąd wzięły się przedziały 
 No i masz:
x∊(−oo; 1) => |x2 − 6x + 8| = x2 − 6x + 8 − bo funkcja jest dodatnia w tym przedziale
|x2 − 6x + 5| = x2 − 6x + 5 − j.w.
x∊(1; 2) => |x2 − 6x + 8| = x2 − 6x + 8 − bo funkcja jest dodatnia w tym przedziale
|x2 − 6x + 5| = −x2 + 6x − 5 − bo funkcja jest ujemna w tym przedziale.
Kolejne przedziały sprawdź sam a potem masz układ równań jak podał ci wreduluspospolitus
No i masz:
x∊(−oo; 1) => |x2 − 6x + 8| = x2 − 6x + 8 − bo funkcja jest dodatnia w tym przedziale
|x2 − 6x + 5| = x2 − 6x + 5 − j.w.
x∊(1; 2) => |x2 − 6x + 8| = x2 − 6x + 8 − bo funkcja jest dodatnia w tym przedziale
|x2 − 6x + 5| = −x2 + 6x − 5 − bo funkcja jest ujemna w tym przedziale.
Kolejne przedziały sprawdź sam a potem masz układ równań jak podał ci wreduluspospolitus

 Tak mniej więcej wygląda wykres twojej funkcji (fioletowe linie) a zielone linie to potencjalne
wartości „m” (y = m) − no i gdzie jest więcej niż 3 przecięcia?
Tak mniej więcej wygląda wykres twojej funkcji (fioletowe linie) a zielone linie to potencjalne
wartości „m” (y = m) − no i gdzie jest więcej niż 3 przecięcia?