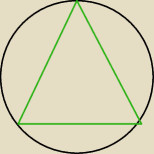
stożek Radek: Stożek, którego pole powierzchni bocznej jest równe 9√10π , jest wpisany w kulę o promieniu 5. Oblicz objętość stożka. Proszę tylko o rysunek, żebym sobie jakoś zaczął

dero2005:

Radek: A przekrój ?

dero2005:

Radek: Dziękuję

Radek: To chyba jednak nic nie dało

Rafał28: R − kuli r − promień podstawy stożka l − tworząca stożka h − wysokość stożka W przekroju osiowym poprowadź wysokość a następnie dwukrotnie z Pitagorasa, dla trójkąta R,R,l oraz trójkąta r, R, h−R Lepszego sposobu nie znalazłem. Trochę liczenia

Rafał28: R − promień kuli

Radek: Coś tam policzyłem, pomożesz mi trochę w geometrii analitycznej ?

Rafał28: Nauczyciel ze mnie kiepski, ale pokaż co tam masz.

Mila: π*r*b=9√10π⇔r*b=9√10 z treści zadania pole przekroju :

	a*b*c
PΔ=		⇔
	4R

	2r*b2		r*b2
PΔ=		=
	4R		10

Narysuj wysokość h w przekroju : Inny sposób na pole przekroju

	1
P=		*2r*h
	2

Wykorzystaj i oblicz V

Radek: Dla jakich wartości parametru α odległość punktu P = (1,2) od prostej y = x+ sin α jest

	1
mniejsza lub równa		?
	√2

Radek: Do tego zadania ze stożka wrócę jutro.

Rafał28: Prostą w postaci ogólnej i wzór na odległość punktu od prostej.

Radek: Jak narysować y=x+sinα ?

Rafał28: W tym zadaniu musisz znać taki wzór. Odległość punktu od prostej. Nie jest to takie trudne jak się wydaje. https://matematykaszkolna.pl/strona/1249.html Podstaw i zobacz co się dzieje dalej.

Radek: −x+y−sinα=0

|−1+2−sinα|		1
	≤		?
√5		√2

Rafał28: mianownik pod wartością względną do poprawki

Radek:

|1−sinα|		1
	≤
√2		√2

Rafał28: ok

Radek: |1−sinα|≤1 /² 1−2sinα+sin²α≤1 −2sinα+sin²α≤0 2sinα−sin²α≥0 sinα(2−sinα)≥0 i co dalej ?

Rafał28: ale sobie komplikujesz życie, ale dobra jakby co jest taki trick =========== |x − 10| ≤ 1 −1 ≤ x − 10 ≤ 1 |x − 10| ≥ 3 x − 10 ≥ 3 lub x − 10 ≤ −3 =========== Zrobiłeś dobrze, teraz podstaw t = sin α i masz zwykłą nierówność z parabolą

Radek: |sinx−1|≤1 sinx≤2 i sinx≤0 Ok ?

Rafał28: Prawie dobrze. W tym drugim zmień znak

Radek: sinx≥0

Rafał28: ok, co dalej?

Radek: Nie wiem jak to rozwiązać sinx∊<0,2> ale co z tym ? <0,1> ?

Rafał28: sin x jakie przyjmuje wartości?

Radek: x∊<−1,1>

Rafał28: W takim razie patrzysz na nierówność sin x ≤ 2 I odpowiadasz na pytanie. Czy dla wszystkich x nierówność jest spełniona?

Rafał28: A tak w ogóle parametr a zamieniliśmy na x, ale nie ważne. Jakby co to a=x

Radek: nie może być mniejsze od −1 ?

Rafał28: Nie zrozumiałeś mnie. Patrz sin x ≤ 2 Oznacza to, że niezależnie co podstawię pod x to lewa strona będzie <−1, 1> a to oznacza, że x∊R i się tego nie rozwiązuje tylko przechodzi do drugiego przypadku. To jest na tej samej zasadzie co x² = −5 (tutaj też x∊R)

Radek: ok to jak drugi przypadek ?

Rafał28: jesteśmy tutaj |sinx−1|≤1 sinx≤2 i sinx≥0

Radek: Tak.

Rafał28: Drugi przypadek to sin x ≥ 0 i należy to rozwiązać. Potrafisz?

Radek: Nie bardzo ?

Rafał28: Rysujesz funkcję y = sin x, albo patrzysz tutaj https://matematykaszkolna.pl/strona/426.html w nierówności sin x ≥ 0 oznacza, że musisz wyznaczyć te argumenty (x−sy), gdzie wykres funkcji sin x jest nad osią OX (na górze) lub równy zero. Odczytujesz to z wykresu.

Radek: Czyli muszę znaleźć wartość dla sinx=0 oraz sinx=1 ?

Radek:

	π
x+2kπ,		+2kπ
	2

Rafał28: Próbujemy dalej Patrzymy na wykres od środka układu współrzędnych. Wykres jest w punkcie (0, 0) i idzie do góry, czyli spełniona jest nierówność (patrz moja ostatnia odpowiedź). Później wykres maleje aż do argumentu x=π. Wobec tego x∊<0, π> jest szukanym naszym przedziałem dla nierówności. Ale to dopiero jeden przedział. Nas interesują wszystkie.

Radek: 0+2kπ, π+2kπ

Rafał28: Ok, teraz spróbuj poskładać to w logiczną całość.

Radek: α∈<0 + 2kπ ,π + 2kπ>

Rafał28: jest OK

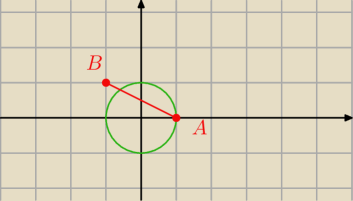
Radek: Dane są punkty A (1,0),B(− 1,1) . Punkt C należy do okręgu o równaniu x²+y² = 1 . Znajdź współrzędne punktu C , tak aby pole trójkąta ABC było największe. Oblicz to pole.

Rafał28: Trzeba wyznaczyć równanie prostej AB a później prostą prostopadłej do AB i taką, że przechodzi przez środek okręgu.

Rafał28: Dlaczego tak? k⊥AB Nazwij sobie punkt przecięcia się prostej AB i prostopadłej do niej (nazwijmy k) jako punkt D. Wtedy prosta k przechodząca przez punkt D przetnie okrąg w punktach E, F. Zauważ, że odcinki DE, DF to są wysokości w trójkącie A, B, C. Pole trójkąta ABC zależy między innymi od wysokości, zatem zależy nam aby ta wysokość była jak największa. Stąd takie rozwiązanie a nie inne.

Radek:

	1		1
Prosta y=−		x−
	2		2

prosta prostopadła przez środek okręgu y=2x Wyjdą dwa rozwiązania i jedno muszę odrzucić ?

Rafał28: Zgadza się. Można odrzucić na oko (ale to dla własnego rozwiązania , Policz długość dwóch wysokości i jedną odrzuć.

Rafał28: a zaraz, prosta y = −¹₂x − ¹₂ to nie prosta AB do poprawki

Radek:

	1		1
AB:y=−		x+
	2		2

Teraz chyba dam radę, jeszcze Cię mogę prosić o pomoc ? Wiem, że późno już.

Rafał28: Jutro mam wolne to pisz

Radek: Nauczyciel z Ciebie dobry więc piszę kolejne za chwilkę

Radek:

	7
Wyznacz równanie okręgu o promieniu		, który przechodzi przez punkty wspólne okręgów o
	5

równaniach x²−4x+y² + 2y + 4 = 0 i x² − 4x + y² + 1 2y+ 19 = 0 .

Rafał28: To najpierw rozsądek podpowiada, żeby wyznaczyć dwa punkty wspólne tamtych okręgów.

Radek: Przyrównać te równania tak ?

Rafał28: można i tak

Radek:

	√3		3
2−		, −
	2		2

	√3		3
2+		, −
	2		2

Rafał28: ok, dalej spróbuj podstawić do równania okręgu te punkty wiedząc, że masz podany promień

Radek: Ok, następne za 5 minut jak będziesz jeszcze

Rafał28: ok

Radek: Rozpatrujemy wszystkie prostokąty o polu równym 6, których dwa sąsiednie boki zawarte są w osiach Ox i Oy układu współrzędnych. Wyznacz równanie krzywej będącej zbiorem tych wierzchołków rozpatrywanych prostokątów, które nie leżą na żadnej z osi układu współrzędnych. Narysuj tę krzywą.

Rafał28: Myślę nad tym. Tzn wiem jak to wygląda, ale jak ci to teraz przedstawić

Rafał28: http://www.zadania.info/d36/2836866 Tutaj masz rozwiązanie. Pisz jak nie rozumiesz.

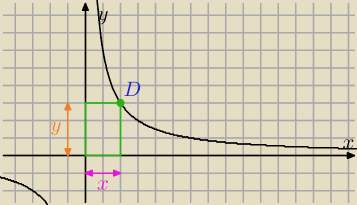
Rafał28: To jest przykład jednego z takich prostokątów. Punkt D ma współrzędne D(x, y). Pole prostokąta

	6
to xy=6, czyli druga współrzędna do y =		.
	x

Radek: Czyli będą 4 takie prostokąty tak ?

Rafał28:

	6
Będzie ich nieskończenie wiele. Twoim zadaniem jest znalezienie tych prostych y =		oraz
	x

	−6
y =		, które zawierają wierzchołek prostokąta nienależący do osi OX, OY
	x

Marcin: Takich prostokątów jest nieskończenie wiele . Każdy dowolny punkt, który spełnia równanie xy=6 lub −xy=6, będzie dawał taki prostokąt Stąd te dwie hiperbole

Radek:

	6		12
Ale czemu funkcja		a nie np		?
	x		x

Rafał28:

	12
Jak podstawisz za x na przykład 5 to masz y =		. Czy twoim zdaniem x * y = 6? Bo pole
	5

każdego z tych prostokątów musi się równać 6.

Radek: ach czyli max wysokość to 6 tak ?

Rafał28: Max pole to 6.

	6
Na przykład dla x = 0,01 mamy y =		= 600
	0,01

Wysokości w takim prostokącie to 0,01 oraz 600 a pole takiego prostokąta dalej jest równe 6

Radek: już rozumiem, dziękuję za pomoc

Rafał28: Trzymaj się

Radek: Jutro też będziesz na forum ?

Rafał28: powinienem

Radek: ok dobranoc.