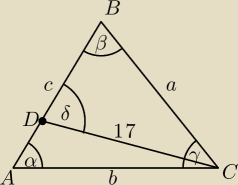
planimetria Arnold: Dany jest trójkąt ABC , w którym sinus kąta alfa/sinus kąta beta=17/25 . Na boku AB leży punkt D taki, że |AD | = 12 , |DB | = 16 oraz |CD | = 17 . Oblicz długość promienia okręgu opisanego na trójkącie ABC .

Arnold: Nie ma nikt pomysłu?

Arnold: Bardzo bym prosił o pomoc w rozwiązaniu.

Rafał28: Oznacz sobie boki |BC| = a, |AC| = b Skorzystaj z twierdzenia sinusów i wyznacz bok a w zależności od b. Następnie oznacz kąt |<BDC| przez δ. Wówczas |<ADC| = π − δ. cos(π−δ) = − cosδ i skorzystaj dwukrotnie z twierdzenia cosinusów dla ΔBDC, ΔADC. Otrzymasz jedno równanie z niewiadomą b.

Arnold: szczerze mówiąc? nie mogę do tego w ogóle dojść...

Arnold: Dany jest trójkąt ABC , w którym sinus kąta A/sinus kąta B=17/25 . Na boku AB leży punkt D taki, że |AD | = 12 , |DB | = 16 oraz |CD | = 17 . Oblicz długość promienia okręgu opisanego na trójkącie ABC. − tak brzmi poprawnie zadanie. wcześniej je podając się pomyliłem z jedną inofmracją

Rafał28: Z tw sinusów (549):

a		b
	=		/((sin α)/b)
sin α		sin β

a		sin α		17
	=		=
b		sin β		25

	17b
a =
	25

−−−−−−−−− Z tw cosinusów (543) dla ΔBDC: a² = 17² + 16² − 2*16*17 * cos δ (17b/25)² = 17² + 16² − 2*16*17 * cos δ

	545		17b2
cos δ =		−
	544		20000

−−−−−−−−−− Z tw cosinusów (543) dla ΔADC: b² = 17² + 12² − 2*12*17 * cos(π − δ) b² = 17² + 12² + 2*12*17 * cos δ

	b2		433
cos δ =		−
	408		408

−−−−−−−−−−

545		17b2		b2		433
	−		=		−
544		20000		408		408

3367b2		3367
	=
1020000		1632

b² = 625 b = 25 (bo b>0)

	17b
a =		= 17
	25

Pole policzysz z tego wzoru: (503) Długość promienia okręgu opisanego na ΔABC policzysz z tego wzoru: (541)

Arnold: Dzięki bardzo

Eta: Mimo wszystko "rachunki" fatalne! ( po licha ? czemu to ma służyć?