romb
bezendu:
Stosunek pola rombu do pola koła wpisanego w ten romb wynosi 8 : π . Oblicz miarę kąta ostrego
rombu.
2aπ=8πr
a=4r
no i co ?
17 lut 18:19
17 lut 18:22
bezendu:
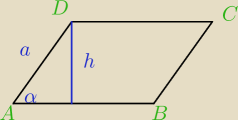
α=30
0
17 lut 18:27
bezendu: ?
17 lut 18:37
Mila:
dobrze.
17 lut 18:39
bezendu: Pomożesz bo mam jeszcze 36 zadań z tego rombu ?
17 lut 18:39
Eta:
17 lut 18:40
bezendu: Oblicz długość boku rombu wiedząc, że prosta poprowadzona przez jeden z jego wierzchołków
odcina na przedłużeniach dwóch jego boków odcinki o długościach 4 i 9
Proszę tylko o rysunek
17 lut 18:46
Mila:
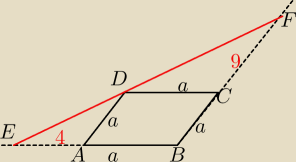
17 lut 18:55
17 lut 18:58
17 lut 18:58
bezendu:
Czy moja odpowiedź jest ok ? Dziękuję za rysunki
17 lut 19:02
17 lut 19:04
bezendu: A z mojej proporcji ?
17 lut 19:05
Eta:
też
17 lut 19:09
bezendu: Dziękuję
17 lut 19:10
bezendu: Długość boku rombu jest równa a , a długości jego przekątnych są równe d1 i d 2 . Oblicz miarę
kąta ostrego rombu jeżeli wiadomo, że a = √d1d2 .
α=300 ?
17 lut 19:18
Eta:
| | 1 | |
P=a2*sinα i P= |
| d1*d2 i a2=d1*d2 |
| | 2 | |
..........
17 lut 19:37
bezendu: Też tak liczyłem.
Jeszcze dwa zadania.
17 lut 19:39
bezendu: Oblicz pole rombu ABCD , wiedząc, że długości promieni okręgów opisanych na trójkątach ABC i
ABD odpowiednio są równe Rc i Rd
Proszę o rysunek do zadania
17 lut 19:46
bezendu: ?
17 lut 20:08
Mila:
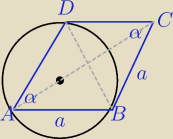
Okręgi nie są potrzebne masz tylko wiedzieć do którego Δ przypisać R.
Skorzystaj z tw. sinusów.α
17 lut 20:24
Mila:
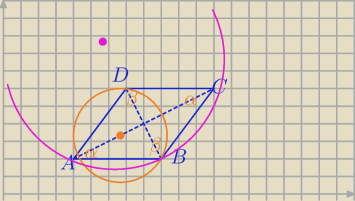
β=180−α
17 lut 20:32
bezendu:
|DB|=2|RC|cosα ?
17 lut 20:37
Mila:
| AC | | AC | |
| =2Rc⇔ |
| =2Rc⇔AC=2Rc sinα |
| sinβ | | sinα | |
Kombinuj dalej
17 lut 21:15
bezendu:
Bardzo dziwne wyniki wychodzą
17 lut 21:21
Eta:
taki ma być
17 lut 21:28
bezendu:
Dziękuję w końcu wyszło.. Na maturze raczej będzie dowód i zadania na optymalizacje ? Gdzie mam
szukać tych drugich zadań ?
17 lut 21:30
Mila:
No i pięknie.
17 lut 21:30
17 lut 21:32
bezendu: Chodzi o takie zadania co trzeba łączyć twierdzenia sinusów+cosinusów+funkcja kwadratowa.
17 lut 21:32
bezendu: Eta geometria analityczna już za mną, chodzi o planimetrię bo z tego jestem najsłabszy.
17 lut 21:34
17 lut 21:34
Eta:
Chciałeś zadania optymalizacyjne
17 lut 21:35
bezendu: Ale z planimetrii
Dziękuję jutro mam w szkole dwie godzinny to przerobię tę zadania
17 lut 21:36
bezendu:
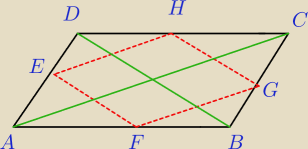
Jeśli mam równoległobok ABCD i wpisano w niego romb tak, że wierzchołki tego rombu leża na
środku ramion tego równoległoboku i boki rombu są równoległe do jego przekątnych
to np to odcinek EF jest połową odcinak AC ?
17 lut 23:26
Eta: tak
17 lut 23:31
bezendu: Ale to by się nie zgadzało, mam podane te długości przekątnych a wynik nie chcę wyjść
AC=26
DB=20
17 lut 23:33
Eta:
Napisz całą treść zadania, bo duchem nie jestem
17 lut 23:35
Mila:
To chyba źle podajesz treść, może podane jest, że boki rombu są równoległe do przekątnych
równoległoboku.
17 lut 23:39
bezendu:
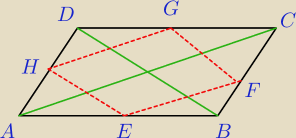
w równoległobok ABCD o przekątnych 26 i 20 wpisano romb kazdy wierzchołek rombu nalezy do
innego boku równoległoboku w taki sposób, że boki rombu są równoległe do przekątnych
równoległoboku. Oblicz długość boku rombu.. Tyle nie chcę gotowca, że mam wszystko policzone i
dokończ tylko obliczenia..
17 lut 23:39
Marcin: cześć bezendu. Która to strona u kiełbasy?
17 lut 23:45
Mila:
Przekątne rombu przecinają się w tym samym punkcie co przekątne równoległoboku i sa
prostopadłe.
Popraw rysunek.
17 lut 23:45
bezendu:
To akurat nie z kiełbasy. Większy kaliber.
17 lut 23:49
Marcin: Kiełbasa to czasem dość duży kaliber którego nie masz szans spotkać na maturze
17 lut 23:51
17 lut 23:56
bezendu: ?
17 lut 23:58
bezendu: Sam to muszę wyprowadzić bo w tamtym dowodzie się gubię.
18 lut 00:00
bezendu:
Muszę wyprowadzać ten wzór czy mogę od razu z niego skorzystać ?
18 lut 15:14
bezendu: ?
18 lut 16:41
Mila:
Masz wyprowadzić .
To nie jest trudne. Podobieństwo.
18 lut 17:03
bezendu: Ale co do czego jest podobne ? Ja tam tylko widzę odcinki które są w skali ?
18 lut 17:23
Mila:
ΔDHG∼ΔDAC bo HG||AC z założenia.
O − punkt przecięcia przekątnych
HG=a− długość boku rombu
| a | | DK | |
| = |
| K− punkt przecięcia HG i DB |
| AC | | DO | |
myśl.
18 lut 17:33
Eta:
18 lut 18:47
bezendu:
18 lut 18:48
Eta:
No nie
to jeszcze tego nie wyprowadziłeś?
18 lut 18:49
bezendu:
Myślę na innym zadaniem.
18 lut 18:50
Mila:
OJJJJJJJJJJJJJJJJ.
18 lut 19:55
bezendu: Wiem, że słabo ale nic nie poradzę
18 lut 19:57
bezendu: ?
18 lut 20:38
Mila:
No co, mamy z Etą pisać?
18 lut 20:56
bezendu: Tak bo sam nie dam rady z tą planimetrią. Jak widać zresztą.
18 lut 20:58
Mila:
To może popatrzymy razem na rozwiązanie , co wskazała Eta i tam zadasz pytanie?
Czy wolisz swój rysunek?
18 lut 21:01
bezendu: Wolę swój rysunek. A czemu nie mogę od razu skorzystać z tego wzoru ?
18 lut 21:07
Mila:
Na średnią harmoniczną?
18 lut 21:22
bezendu:
Tak.
18 lut 21:26
Mila:
Dlatego, że masz w poleceniu oblicz długość boku rombu.
Czy zapis z 17:33 jest dla Ciebie jasny?
18 lut 21:35
bezendu: Tak.
18 lut 21:36
Mila:
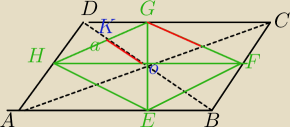
HG||AC z zał.
|HG|=a dł. boku rombu.
podstawiam do (1)
a*|DB|=|AC|*|DB|−|AC|*a
a*|DB|+|AC|*a=|AC|*|DB|
a*(|DB|+|AC|)=|AC|*|DB|
cnw
18 lut 21:59
bezendu:
Czemu tu znalazł się KO ?
18 lut 22:03
Mila:
|KO| jest częścią przekątnej DB i jednocześnie odcinkiem zawartym w rombie.
18 lut 22:08
bezendu: To chyba jeszcze nie na moją głowę
18 lut 22:10
Mila:
Wynik taki jak w odpowiedzi?
18 lut 22:15
bezendu: Wynik się zgadza.
18 lut 22:17
Hajtowy: Black magic
18 lut 22:24
Mila:
Hajtowy nie siej defetyzmu. Możecie sobie to zadanie odpuścic.
18 lut 22:26
Eta:
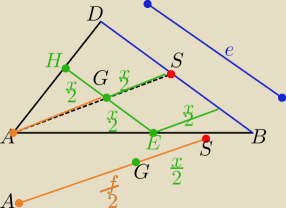
x −−− dł. boku rombu , e,f −−długości przekątnych
z podobieństwa trójkątów AEH i ABD
| | x | | 0,5f−0,5x | | x | | f−x | |
|
| = |
| ⇒ |
| = |
| ⇒ xf=ef−ex ⇒ x(f+e)=ef |
| | e | | 0,5f | | e | | f | |
| | ef | |
x= |
| −−− połowa średniej harmonicznej długości przekątnych |
| | f+e | |
18 lut 22:27
bezendu: A jak takie będzie w maju ?
18 lut 22:27
Eta:
To już będzie dla Ciebie "
malutki 
" ( czyt. "pikuś"
18 lut 22:32
Mila:
Jeszcze w trapezie jeden z odcinków też ma długość związaną ze średnia harmoniczną.
Przećwicz i nic Cię nie zaskoczy.
18 lut 22:37
bezendu:
W jakim trapezie ?
18 lut 22:38
18 lut 22:39
Mila:
Mam podać treść, ? może Eta ma pod ręką.
18 lut 22:39
Mila:
Dzisiaj też miałam taki przyjemny wpis. Co zrobić, zapamietać osóbkę.
POzdrawiam.
18 lut 22:41
bezendu:
Tak proszę o to zadanie.
18 lut 22:51
Mila:
Podstawy trapezu mają długość a i b. Przez punkt przecięcia przekątnych trapezu poprowadzono
prostą równoległą do podstaw. Ta prosta przecina ramiona trapezu w punktach M i N.
Wykaż, że długość odcinka MN jest średnią harmoniczną liczb a i b.
18 lut 22:52
bezendu:
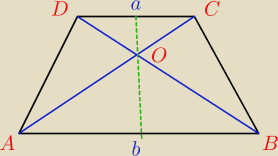
I mogę napisać jeszcze, że ΔDOC i ΔAOB są podobne. I tylko tyle niestety.
18 lut 22:58
Mila:
Brak punktów M i N. Zostaw do jutra.
18 lut 23:04
Mila:
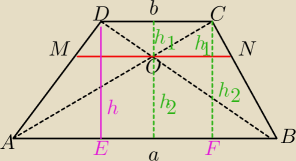
Z. AB||DC, MN||AB⇔MN||DC
| | a | |
1) ΔABO∼ΔDCO w skali k= |
| ⇔ |
| | b | |
2)ON||AB z założenia ⇔
ΔONC∼ΔABC⇔
| | a | | b+a | |
|CF|=h=h1+h2=h1+ |
| *h1=h1* |
| ⇔ |
| | b | | b | |
cnw
19 lut 16:36
Mila:
Co jest niejasne?
19 lut 18:35
bezendu:
Nie rozumiem czemu akurat jest to liczone z trójkątów ΔONC∼ΔABC ?
19 lut 18:46
Mila:
Bo ON jest częścią MN i jest w takim Δ ,że możemy wykorzystać podobieństwo do ΔABC.
19 lut 19:02
bezendu: Tylko skąd mam wiedzieć które trójkąty brać ?
19 lut 19:10
jacuś: Mila ty jeszcze Uczysz w szkole?
19 lut 19:22
Mila:
Masz szukać takich trójkątów z których możesz coś obliczyć, czasem kierujesz się konkretnym
kątem, czasem podobieństwem, czasem korzystasz z tw. Pitagorasa, czasem porównujesz pola.
19 lut 19:29
Mila:
Jacuś nie udzielam szczegółowych odpowiedzi na pytania osobiste.
Możesz zadać pytanie merytoryczne.
19 lut 19:30
jacuś: Dziwi mnie tylko to skąd masz tyle czasu do spędzania na forum
19 lut 19:34
jacuś: zadanie też mam tylko muszę poszukać treści
19 lut 19:35
Mila:
Postaram się w takim razie mniej czasu spędzać na forum.
19 lut 19:36
jacuś: moje zadanie
Mamy wielomian
W(x)=a
1x
5+a
2x
4+a
3x
3+a
4x
2+a
5x
Dodatkowo wiadomo, że
W(3)=2
W(6)=4
W(12)=8
W(15)=10
Oblicz W(9)
19 lut 19:50
bezendu: Mila nie rób tego proszę ! 19:36
19 lut 19:54
ZKS:
Z interpolacji to zrób.
19 lut 20:02
ZKS:
Mila nie przejmuj się głupimi zaczepkami to co robisz jest świetne więc rób do dalej.
19 lut 20:03
bezendu: A tak wgl ta załóż sobie swój temat kolego..
19 lut 20:03
19 lut 20:16
Mila:
Witaj
ZKS.
19 lut 20:17
jacuś: Co to jest interpolacja? ja Jestem w liceum.
Mila na tej stronie tego nie ma
Przepraszam Jeśli Cię uraziłem
19 lut 20:18
ZKS:
Hej
Mila.
19 lut 20:25
Mila:
Masz skorzystać z informacji.
I kto Ci dał takie zadanie?
Myślę, aby zrobić nie napracować się zbyt dużo.
19 lut 20:28
bezendu:
To zadanie mam w arkuszu. Tak samo jak to z tym trapezem.
19 lut 20:29
Mila:
O którym zadaniu mówisz Bezendu.
19 lut 20:32
jacuś: Zadanie mam od mojej nauczycielki
19 lut 20:33
bezendu: Pomyliłem watki chodziło mi o to zadania z kątem.
Jacuś załóż nowy temat bo robisz tutaj bałagan. Tutaj jest planimetria. !
19 lut 20:35
jacuś: a Jak to zrobić?
19 lut 20:35
ZKS:
| | 2 | |
Jeżeli się nie pomyliłem to W(9) = 6. Twój wielomian jest postaci W(x) = |
| x. |
| | 3 | |
19 lut 20:40
Mila:
Wskazówka:
W(x)=x*(a
1x
4+a
2x
3+a
3x
2+a
4x+a
5)=x*Q(x)
| | 4 | | 2 | |
W(6)=6*Q(6)=4⇔Q(6)= |
| ⇔Q(6)= |
| |
| | 6 | | 3 | |
W(9)=9*Q(9)=..?
19 lut 20:42
Mila:
No i Jacuś poszedł. A rozwiązania dwa czekają.
19 lut 20:53
jacuś: Czytam i nic nie rozumiem
ale czytam
19 lut 20:56
Mila:
Czego nie rozumiesz?
W którym miejscu?
19 lut 21:00
ZKS:
Świetne rozwiązanie
Mila jak tego się nie rozumie to przykro ale łatwiej wyjaśnić się
chyba nie da.
19 lut 21:02
Mila:
Tu odpowiedz, a potem załóż nowy wątek:
Klikasz DODAJ ZADANIE potem dostaniesz komunikat, poradzisz sobie.
19 lut 21:02
jacuś: Podobno wynik to około 1000 ale nie wiem skąd się bierze
19 lut 21:04
ZKS:
Na pewno nie do tego zadania taki wynik.
19 lut 21:13
jacuś: Wiem co mam źle
Dzięki
jeszcze mam jedno takie tylko trochę inaczej napisane założę inny wątek
19 lut 21:38
bezendu: W końcu.
19 lut 21:44
bezendu: Mogę prosić o wytłumaczenie tego dowodu jeszcze raz bo nic nie rozumiem z tego nadal.
19 lut 23:10
Mila:
Z trapezem?
19 lut 23:29
bezendu: Tak.
19 lut 23:30
Mila:
To może jutro, teraz kończę.
Dobranoc.
19 lut 23:47
bezendu: Dobranoc.
P.S czytam wszystkie posty
19 lut 23:50
bay:
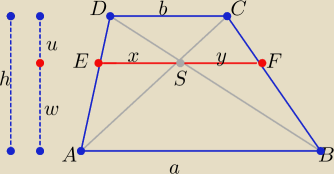
Czy o ten dowód pytasz?
h=u+w
Z podobieństwa trójkątów
ABD i EDS oraz ABC i CFS
| a | | h | | a | | h | | a*u | | a*u | |
| = |
| i |
| = |
| ⇒ x= |
| i y= |
| ⇒x=y |
| x | | u | | y | | u | | h | | h | |
| | a | | w | | a*u | |
z podobieństwa trójkątów ABS i DCS : |
| = |
| ⇒ w= |
| |
| | b | | u | | b | |
| | a*u | | 2a*u | | 2a*u | | 2ab*u | |
|EF|=2x =2* |
| = |
| = |
| = |
| = |
| | h | | u+w | | | | bu+au | |
| | 2ab | |
|EF|= |
| −−− średnia harmoniczna długości podstaw trapezu |
| | a+b | |
19 lut 23:51
ZKS:
W(x) = x * Q(x)
| | 2 | |
Q(x) = (x − 3)(x − 6)(x − 12)(x − 15) + |
| |
| | 3 | |
| | 2 | |
W(x) = x * [(x − 3)(x − 6)(x − 12)(x − 15) + |
| ] |
| | 3 | |
| | 2 | |
W(9) = 9 * [6 * 3 * (−3) * (−6) + |
| ] = 2922 |
| | 3 | |
19 lut 23:57
ZKS:
Przepraszam bezendu że Ci piszę w Twoim temacie ale tylko napisałem dla
informacji Mili.
19 lut 23:58
bezendu: Tak o ten.
20 lut 00:00
bezendu: Eta ale czemu te trójkąty bierzesz?
20 lut 00:03
bay:
No jak czemu? .......... bo są podobne
Idź już do spania
jutro jak będziesz wypoczęty , to jeszcze raz przeanalizujesz ten dowód
Mila też Ci wyjaśniała , w ten sam sposób
( tylko mnie nie chciało się pisać indeksów h
1 i h
2 .... oznaczyłam w i u
20 lut 00:11
bezendu: Do 02:00 mam jeszcze kilka zadań pomożesz ? Dowód zostawię na jutro.
20 lut 00:12
bay:
I nie jestem Etą ! ........ "bay, bay"
20 lut 00:12
bezendu: Ok to bay pomożesz ?
A ciekawe co z Etą
20 lut 00:13
bay:
Pisz zadanie
( ja idę na herbatkę )
20 lut 00:19
Bogdan:
dla
bay
20 lut 01:05
Mila:
ZKS, dziękuję. Ja napisałam :
| | 2 | |
W(9)=9*[a1*(9−3)(9−6)(9−12)(9−15)+ |
| ] |
| | 3 | |
Jak ustaliłeś, że a
1=1?
20 lut 16:02
Eta:
dla
Bogdana
20 lut 22:09
bezendu:
Proszę jeszcze raz o wyjaśnienie zadania z rombem
20 lut 22:24
Eta:
czyt. 18 luty 22:27
20 lut 22:25
Mila:
W którym miejscu nie rozumiesz ?
20 lut 23:12
bezendu:
(**) CF=?
20 lut 23:14
bezendu: ?
20 lut 23:50
Mila:
CF to wysokość trapezu.
Częścią tej wysokości jest h
1− wysokość w ΔCON,
h=h
1+h
2
te dwie wysokości h
1 i h
2 występują w ΔAOB i DOC, a ponieważ te Δsą podobne, ( co już wiesz
na pewno !?) to
h
2=...
analizuj dalej, czytaj, czytaj patrz na rysunek i zapisy.
Trapez ma Ci się śnić ze swoimi podobieństwami w nocy o północy. To bardzo ważna figura
geometryczna.
21 lut 00:00
Mila:
Właśnie wybija pólnoc.
DOBRANOC
21 lut 00:00
bezendu: Dziękuję, już zrozumiałem teraz postaram się wrócić do rombu i tego zadania z bryłą. Są jeszcze
jakieś figury z tą średnią ?
21 lut 00:01