prawdo
Radek:
Wytłumaczył by ktoś prawa de morgana na zbiorach i diagramy venna ?
16 lut 17:55
Mila:
To już przerabialiśmy.
Podaj konkretne zadania.
16 lut 18:15
Radek:
Proste zadania tak a teraz mam trudniejsz
| | 1 | |
Obliczyć P(A'∩B') mając P(A')= |
| |
| | 3 | |
| | 1 | |
P(B')= |
| oraz P(A∩B)=0,5 |
| | 4 | |
16 lut 18:19
Mila:
1) (A∪B)' =A'∩B'
2) (A∩B)' =A'∪B' zapamiętaj.
(A'∩B')'=A∪B z (2)
Próbuj dalej:
P(A')=1−P(A)
P(A)=1−P(A')
16 lut 18:36
Radek: Ale czemu (A'∩B')' ?
16 lut 18:44
Mila:
Patrzysz co możesz obliczyć na podstawie danych.
P(A), P(B),P(A∪B)
P((A'∩B')')=P(A∪B) związek między A'∩B" i A∪B
P(A∪B)=P(A)+P(B)−P(A∩B)
| | 2 | | 3 | | 1 | | 2 | | 1 | | 11 | |
P(A∪B)= |
| + |
| − |
| = |
| + |
| = |
| |
| | 3 | | 4 | | 2 | | 3 | | 4 | | 12 | |
| | 11 | | 1 | |
P[(A∪B)']=1− |
| = |
| =P(A'∩B') |
| | 12 | | 12 | |
16 lut 18:59
Radek: Ale skąd te związki ?
16 lut 19:01
Mila:
Która linijka?
16 lut 19:07
Radek:
W zadaniu mam P(A'∩B') a Pani P(A'∩B')' ?
16 lut 19:09
Mila:
To popatrz na ostatnią linijkę 18:59.
16 lut 19:17
Radek:
Ale skąd są te własności ? Ja nie potarfię ich tak rozpisywać.
16 lut 19:21
Mila:
(A')'=A
(A∪B)'=A'∩B'
(A∩B)'=A'∪B'
(A'∩B')'=(A')'U(B')'=A∪B
P(A∪B) mogłeś na podstawie danych obliczyc, ale to jest zadrzenie przeciwne do A'∩B'
((A∪B)'=A'∩B')
zatem
1−P(A∩B)=P(A'∩B')
16 lut 19:55
Radek: (A'∩B')=A∪B ?
16 lut 19:56
Mila:
(A'∩B')'=A∪B ?
16 lut 19:59
Radek:
ale bez tej kreski za nawiasem
16 lut 20:00
Mila:
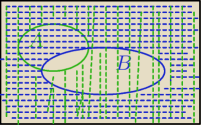
A' zielone zakreskowane
B' niebieskie zakreskowane
A'∩B'≠AUB
16 lut 20:21
Radek:
Spróbuje to zrozumieć choć wcale nie idą mi te zadania.
16 lut 20:24
16 lut 20:26
Mila:
16 lut 22:07
Radek:
Ma Pani jakiś link z tymi zależnościami bo nie mogę wywnioskować co z czego
16 lut 22:08
Mila:
18:36 dwa niebieskie wzory.
i własności prawdopodobieństwa.
Pisz zadania.
16 lut 22:31
Radek:
O zdarzeniach losowych A i B wiadomo, że P (A∪B)=0,9, P(A∩B )=0,3 i P(A∪B′)= 0,5.Oblicz P
(A′∪B ) .
16 lut 22:33
16 lut 22:33
Mila:
A∪B' czy A∩B' ?
16 lut 22:36
Radek:
Dobrze przepisałem
16 lut 22:40
Mila:
Zaraz, będą dwa rysunki.
16 lut 22:51
Eta:
16 lut 22:53
Mila:
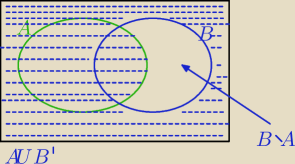
P(AUB')=0,5
Możemy obliczyć
P(B\A)=1−P(AUB')=1−0,5=0,5
Analogicznie :
P(A\B)=1−P(A'UB) zaraz to narysuję.
P(AUB)=P(A\B)+P(A∩B)+P(B\A)
0,9=P(A\B)+0,3+0,5
P(A\B)=0,1
0,1=1−P(A'UB)⇔
P(A'UB)=0,9
16 lut 23:03
Mila:
Może sam narysujesz A'UB ?
16 lut 23:03
Radek:
Dobrze spróbuje
16 lut 23:05
Radek: ?
16 lut 23:36
Mila:
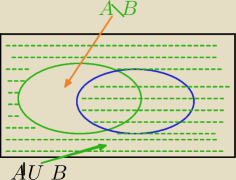
P(A'∪B)=1−P(A\B)
16 lut 23:40
Radek:
P(A'∪B)=P(B)−P(A)−P(A∩B) ?
16 lut 23:42
Mila:
Radek jak obliczysz pole tego zakreskowanego obszaru?
16 lut 23:45
Radek:
od 1−P(A\B) a moje rozwiązanie 23:42 ?
16 lut 23:47
Mila:
23:42 źle, obliczaj, zobaczysz co wyjdzie.
23:47 dobrze.
16 lut 23:49
Radek:
Rysuje to wszystko ale wychodzą mi inne rozwiązania w zadaniach.
16 lut 23:50
Mila:
Widocznie błędnie interpretujesz.
16 lut 23:54
Radek: To jeszcze jutro wstawię kilka przykładów i potem nierówności Dobranoc
16 lut 23:56
Mila:
Dobranoc
17 lut 00:01
Radek: Wystarczy pamiętać te wzory które Pani podała ?
17 lut 17:40
Radek: ?
17 lut 18:28
Radek: ?
17 lut 20:38
Mila:
de Morgana ? Tak. I wszystkie własności prawdopodobieństwa.
17 lut 20:40
Radek: To podpowie mi Pani który mam kiedy stosować, zaraz dam zadanie.
17 lut 20:42
Radek: a warunkowe też jest ?
17 lut 20:50
Radek:
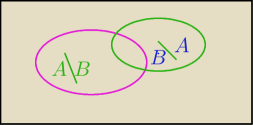
Czy P(A∩B')=1−P(B\A) ?
17 lut 21:27
Mila:
Warunkowego nie ma.
A∩B'=A\B⇔P(A∩B')=P(A\B)
17 lut 21:34
Radek:
Ale B' to jest wszystko oprócz P(B) ?
17 lut 21:37
zawodus: B' to wszystko oprócz B
17 lut 21:38
Radek:
Czyli 1−P(B) ?
17 lut 21:41
Mila:
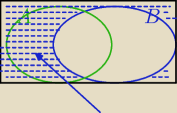
A∩B'=A\B
17 lut 21:43
Radek: A no tak, zaraz napisze jak wyszło całe zadanie.
17 lut 21:44
Radek:
| | 3 | |
Niech A i B będą zdarzeniami losowymi zawartymi w Ω Wiadomo, że P(A∩B')= |
| |
| | 10 | |
| | 1 | | 9 | |
P(A∩B)= |
| P(A∪B)= |
| Oblicz P(A) i P(B) |
| | 5 | | 10 | |
?
17 lut 21:51
17 lut 21:55
Mila:
Dobrze.
17 lut 21:56
Radek: Jak Pani jeszcze będzie na forum to wstawię jeszcze kilka
17 lut 21:57
Mila:
bo
P(AUB)=P(A\B)+P(A∩B)+P(B\A)
17 lut 22:00
Radek: Może Pani podać jakiś przykład żeby tylko rozpisać bez liczenia. ?
17 lut 22:16
Mila:
| | 1 | | 2 | |
O zdarzeniach losowych A i B wiemy, że: P(A ) = |
| , P (B) = |
| , |
| | 2 | | 3 | |
Oblicz:
P(A ∩ B)
P(A ∖B )
17 lut 22:40
Radek:
Chodziło raczej o użycie de morgana
17 lut 22:58
Mila:
Jutro poszukam.
17 lut 23:00
Radek: Dziękuję
17 lut 23:01
Mila:
Dane P(A'∩B')=0,25
Oblicz P(AUB)
18 lut 14:53
Radek:
P(A'∩B')=P(A∪B)=0,25
18 lut 14:59
Mila:
Nie. Pomyśl, narysuj diagram.
18 lut 15:22
Radek:
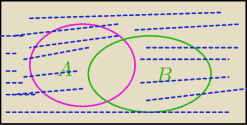
P(A'∩B')=1−P(A∩B) ?
18 lut 15:26
Saizou :
zielone to A'∩B', zatem AUB=....
18 lut 15:30
wredulus_pospolitus:
15:26 ... bzduuura
1−P(A∩B) = P( (A∩B)' )
18 lut 15:32
Radek: Czemu bzdura ?
18 lut 15:32
Saizou :
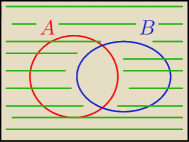
zielone to: Ω−(A∩B)
18 lut 15:36
Radek:
Ale P(A'∩B') to jest to wszystko oprócz P(A∪B) ?
18 lut 15:40
wredulus_pospolitus:
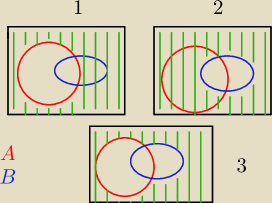
1 −−− A'
2 −−− B'
3 − A'∩B'
18 lut 15:42
Saizou :
zobaczmy rysunek z godz: 15:30
A'∩B' to co jest zielone zatem AUB=Ω−( A'∩B')⇒P(AUB)=1−P( A'∩B')⇒P( A'∩B')=1−P(AUB)
a zobacz co napisałeś o 15:26
18 lut 15:44
Mila:
Radek, co Ty na to?
18 lut 15:46
Radek: 15:40 jest ok ?
18 lut 15:49
Saizou : 
18 lut 15:49
wredulus_pospolitus:
tak ... 15:40 jest ok
18 lut 15:49
Radek: To proszę o kolejny przykład do rozpisania.
18 lut 15:53
Mila:
P(AUB)=?
18 lut 15:55
Radek: No tak ?
18 lut 15:58
Mila:
Nie odpowiedziałeś do poprzedniego zadania.
18 lut 16:17
Mila:
zadanie 2.
P(A∩B')=P(B∩A'),
P(AUB)=0,75, P(A∩B)=0,25.
Oblicz:
P(B)=?
P(A\B)=?
18 lut 16:20
18 lut 16:24
Radek:
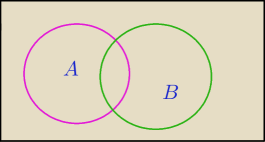
P(B)=P(A∪B)−P(A\B)+P(A∩B)
Ale za mało danych jest ?
18 lut 16:32
Mila:
Wystarczająco, tylko wykorzystaj wszystkie.
18 lut 16:37
Mila:
Jak inaczej zapiszesz ?
A∩B'=
B∩A' =
?
18 lut 16:47
Radek: P(A\B)=P(A∩B')
P(B\A)=P(B∩A')
18 lut 16:49
Mila:
No właśnie, to :
P(AUB)=P(A\B)+P(A∩B)+P(B\A) bo te trzy zbiory (A\B), (A∩B), P(B\A) sa rozłączne.⇔
?
18 lut 16:55
Radek: Skąd mam wiedzieć kiedy one są rozłączne ?
18 lut 16:57
Mila:
Z definicji A\B, B\A, A∩B.
18 lut 17:01
Radek: To nie wiem jak to dokończyć.
18 lut 17:12
Mila:
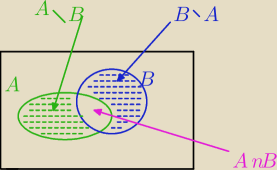
Te trzy zbiory są rozłączne i w sumie dają AUB.
18 lut 17:13
Mila:
P(AUB)=P(A\B)+P(A∩B)+P(B\A) ⇔P(A\B)=P(B\A) =x
0,75=x+0,25+x
Dokończ
18 lut 17:14
Radek: Nigdy bym tego nie rozwiązał
2x=0,5
x=0,25
18 lut 17:21
Mila:
a P(B)=?
18 lut 17:22
Radek: P(B)=0,75
18 lut 17:24
Mila:
| | 1 | |
3) Wiadomo, że P(AUB)=0,5, P(A)=P(A∩B)= |
| . |
| | 3 | |
Oblicz:
P(B)=?
P(B\A)
Teraz zostawiam Cię, będę później.
18 lut 17:25
Mila:
17:21 dobrze.
17:24 źle
P(B)=P(B\A)+P(A∩B) patrz na diagram.
18 lut 17:27
18 lut 17:28
Mila:
zadanie 3 dobrze.
18 lut 20:13
Radek:
W piątek mam z tego sprawdzian.
18 lut 20:14
Mila:
Rozwiązuj teraz innego typu zadania z prawdopodobieństwa.
w zad. 2
P(B)=0,5 zobacz, swój błąd.
18 lut 20:20
Radek: I z innymi nie mam takiego problemu jak z tymi działaniami na zbiorach.
18 lut 20:21
Mila:
Wypisuj ze swojej ksiązki, może coś poradzimy razem.
18 lut 20:21
Radek: Dobrze za 10 minut bo idę teraz na kolację.
18 lut 20:24
Radek:
Skąd mam wiedzieć kiedy zdarzenia się wykluczają ? Skąd to wnioskować
18 lut 20:59
Mila:
Nie mają części wspólnej.
18 lut 21:02
Radek:
| | 1 | | 1 | |
Dane są dwa takie zdarzenia A i B , że P (B) ≤ |
| i P (A ∩ B ) ≥ |
| . Czy może |
| | 3 | | 10 | |
| | 4 | |
zachodzić równość P(B ∖ A ) = |
| ? Odpowiedź uzasadnij |
| | 15 | |
O co chodzi z tymi nierównościami ? Pełno mam ich w arkuszach.
18 lut 21:18
Mila: patrz rys.17:13
| | 1 | | 1 | | 7 | |
P(B\A)=P(B)− P(A∩B) ≤ |
| − |
| = |
| |
| | 3 | | 10 | | 30 | |
| | 7 | | 4 | |
P(B\A)≤ |
| i nie może być równe |
| bo |
| | 30 | | 15 | |
18 lut 21:33
Radek: Tu nie wiem skąd co się wzięło. Może jednak najpierw zadania z kombinatoryki.
18 lut 21:42
Radek:
Z cyfr 0...9 tworzymy liczby sześciocyfrowe Ile jest takich liczb, w których dziewiątka
występuję dokładnie 3 razy i żadna z pozostałych cyfr nie powtarza się.
?
18 lut 22:01
Mila:
1) Inaczej: bo może Ci wpaść zero na pierwszą pozycję, trzeba dać 9 na pierwszą pozycję.
18 lut 22:25
Radek:
Jak może wypaść zero skoro pierwsza wybieram z na 3 miejsca 9 ?
18 lut 22:27
Mila:
To zera nie będzie w tych liczbach?
(999xxx) Dla dziewiątek wybierasz 3 miejsca np. tak
(xx999x) zostają Ci do wyboru cyfry {0,1,2,3,4,5,6,7,8} i piszesz ,że z 9 wybierasz ...itd, to
może Ci zero wskoczyc na 1 miejsce. Prawda?
18 lut 22:31
Radek:
Ale pierwsze 3 miejsca obsadzam 9 więc nie będzie zera.?
18 lut 22:33
18 lut 22:34
Mila:
| | | |
Jeżeli na 3 pierwszych miejscach 9 to po co piszesz | , to jest bez sensu. |
| | |
18 lut 22:36
Radek:
To jak to zapisać, żeby miało sens ? Tego nie robi się na przypadki ?
18 lut 22:37
Mila:
Podałam linka, tam wytłumaczyłam. Jeśli nie zrozumiesz, to będziemy wyjaśniać.
18 lut 22:38
Radek:
Napisałem w tamtym temacie.
18 lut 22:50
Mila:
Nie ukazał się tam Twój komentarz.
18 lut 22:53
Radek: Napisałem przecież i potem jeszcze ''?''
18 lut 22:55
Mila:
Czy już rozumiesz?
18 lut 23:00
Mila:
9 jest na pierwszym miejscu, wybierasz 2 miejsca dla dwóch pozostałych dziewiątek.
18 lut 23:02
Radek: Niestety nie rozumiem
18 lut 23:05
Mila:
Masz sytuację:
1) (9,xxxxx) na pierwszym miejscu jest 9, mamy gwarancję, że nie wpadnie nam tu zero.
| |
wybieram dwa miejsca dla dwóch dziewiątek, na pozostałe 3 miejsca wybieram kolejno |
| |
cyfry ze zbioru{0,1,2,3,4,5,6,7,8}
na 9*8*7 sposobów
2) druga sytuacja
(C,xxxxx) na pierwszą cyfrę wybieram jedną z {1,2,3,4,5,6,7,8}
wybieram 3 miejsca dla dziewiątek, na pozostałe 2 miejsca wybieram kolejno z 8 cyfr pozostałych
18 lut 23:14
Radek:
''Wybieramy dwa miejsca dla dziewiątek''
Ale mają być trzy 9 i liczba sześciocyfrowa ?
18 lut 23:16
Mila:
No przecież jedną 9 umieściłam na pierwszym miejscu! Zostały 2 dziewiątki do rozmieszczenia.
Licz aniołku.
(9,x99xx)
18 lut 23:19
Radek:
| | | |
Teraz widzę a czym różni się zapis | *9*8*7 od tego który podała Pani dla pierwszej |
| | |
sytuacji skoro i tak wybieram 9
18 lut 23:26
Mila:
Tym, że Twoje trzy 9 mogą wskoczyć na dalsze miejsca, a na pierwsze wejdzie 0.
18 lut 23:37
Radek: Już zrozumiałem, po czasie ale zrozumiałem Dziękuję bardzo
18 lut 23:38
Mila:
No to dobrze.
Dobranoc.
18 lut 23:41
Radek: Dobranoc.
18 lut 23:43
Radek:
Powinno
9 mar 19:01
