Matura
Godzio: Maturzyści
Chcecie jakieś ciekawsze zadanka, żeby się pogłowić

?
8 lut 19:57
exevan: ciekawsze

nawet te proste są dla mnie ciężkie co dopiero te "ciekawsze"
8 lut 19:58
Marcin: Ja bym poprosił, ale nie wiem czy dzisiaj będę mieć głowę się głowić

Poziom też prosiłbym
maturalny

8 lut 19:58
Godzio:
To na początek coś prostego.
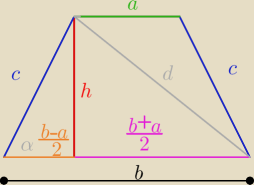
Zadanie 1
W trapezie równoramiennym o polu P dane są promień okręgu opisanego r oraz suma długości obu
podstaw s. Obliczyć obwód tego trapezu. Podać warunki rozwiązywalności zadania. (inaczej,
kiedy zadanie ma sens )
8 lut 20:02
5-latek: Skoro
Godzio zalozyl temat to sie mu nie wcinamy i on daje zadania

8 lut 20:03
Ajtek:
Ciekawe zadanko, ciekawe

.
8 lut 20:19
Ajtek:
A tak w ogóle to cześć
Godzio 
.
8 lut 20:19
Godzio:
Witam

8 lut 20:23
Godzio:
Zadanie 2
Znaleźć wszystkie wartości parametru rzeczywistego m, dla których pierwiastki trójmianu
kwadratowego f(x) = (m − 2)x2 − (m + 1)x − m spełniają nierówność |x1| + |x2| ≤ 1.
Zadanie 3
Dla jakich wartości rzeczywistego parametru p równanie (p − 1)x4 + (p − 2)x2 + p = 0 ma
dokładnie dwa różne pierwiastki.
8 lut 21:00
Ajtek:
Oba do wciągnięcia nosem

.
8 lut 21:07
Godzio:
Ja trudnych zadań nie daje

8 lut 21:08
Marcin: | | 1 | |
W pierwszym założeniu zad 2 wyjdzie, że x∊(−∞; |
| ) v (1;+∞) |
| | 5 | |
A jak mogę zapiać inaczej |x
1| + |x
2| ≤1?
8 lut 21:11
Godzio:
Marcin na tym polega trudność zadania, żeby to jakoś przekształcić, pomyśl

A o jakim założeniu mówisz ? I chodzi Ci o m (a nie o x

) tak ?
8 lut 21:13
Marcin: Tak, tak. o m
8 lut 21:14
Marcin: | | −b | |
To nie będzie chyba | |
| | ≤ 1, prawda? Byłoby jakieś za proste. |
| | a | |
8 lut 21:15
Godzio:
I wiem, że to dziwnie wygląda, ale Δ ≥ 0. Nie nie jest powiedziane, że x
1 ≠ x
2 
8 lut 21:16
Godzio:
Zdecydowanie nie

8 lut 21:16
Lorak: 3.
Dla jakich wartości rzeczywistego parametru p równanie (p − 1)x
4 + (p − 2)x
2 + p = 0 ma
dokładnie dwa różne pierwiastki.
Na początek sprawdzę czy istnieją 2 różne rozwiązania dla p=1 lub p=2.
Dla p=1 rozwiązania to x=−1 oraz x=1, czyli p=1 spełnia warunki zadania.
Dla p=2 dostajemy sprzeczność.
(p − 1)x
4 + (p − 2)x
2 + p = 0
x
2=t, t≥0
(p − 1)t
2 + (p − 2)t+ p = 0
1) Δ=0 i t
0>0 2) Δ>0 i t
1t
2<0
Δ=(p−2)
2−4p(p−1)=−3p
2+4
1) Δ=0
−3p
2+4=0
t
0>0
−2(p−2)(p−1)>0
p∊(1;2)
| | 2√3 | |
Łącząc Δ=0 i t0>0 dostajemy p= |
| |
| | 3 | |
| | 2√3 | | 2√3 | |
2) Δ>0 ⇔ p∊ (−∞; |
| )∪( |
| ;∞) |
| | 3 | | 3 | |
| | p | |
t1t2<0 ⇔ |
| <0 ⇔ p(p−1)<0 ⇔ p∊(0;1) |
| | p−1 | |
Brak części wspólnej.
Coś mi gdzieś nie gra, ale nie wiem co

8 lut 21:30
Ajtek:
Godzio mi kiedyś zasunąłeś dowód dla wartości sin72
o bodaj

8 lut 21:33
Godzio:
Δ > 0 ⇒ p ∊ ... (tylko tu jest błąd reszta jest ok

)
8 lut 21:38
Godzio:
A to było trudne

?
8 lut 21:39
Ajtek:
A weź przestań

. Zanim wpadłem na pomysł....
8 lut 21:40
Saizou : a obwód z zadania nr. 1 to nie czasem
8 lut 21:42
Godzio:
No właśnie, jak się wpadnie na pomysł to jest banalne zadanie

. To pomysł jest trudny, a nie
zadanie

8 lut 21:42
Ajtek:
Skoro pomysł jest trudny, to i zadanie nie jest proste

8 lut 21:43
Godzio: Saizou bardzo dobrze, a warunki rozwiązywalności zadania

?
8 lut 21:43
Mila:
Ajtek kąt 72o to wdzięczny temat, pięciokąt foremny, złoty podział odcinka.
Godzio dba o Twój rozwój.
8 lut 21:43
Saizou : jeszcze nie, bo się skupiłem tylko na razie na obwodzie

8 lut 21:43
Lorak: aa..minus tam zgubiłem

8 lut 21:44
Ajtek:
Mila to było dobre 2 i pół roku wstecz. Jak Godzio maturę zdawał, jakoś ten okres.
8 lut 21:44
Saizou : w sumie to co do warunków to nie mam pojęcia
8 lut 21:47
Godzio:
Żeby dać jakąś wskazówkę, musiałbym zobaczyć jak rozwiązujesz, więc jak chcesz to napisz, albo
kombinuj nad warunkiem

8 lut 21:50
Ajtek:
P>0

8 lut 21:50
Godzio:
Pomijamy trywialne założenia

8 lut 21:51
Saizou : to może ja napiszę, ale jedynym sensownym warunkiem jak dla mnie byłoby napisanie że
8 lut 21:51
Hajtowy: P(A) =
Godzio > 0

Wygrałem?

8 lut 21:53
Ajtek:
Hajtowy nie

P(A)=
Godzio=1

8 lut 21:54
Saizou :
8 lut 21:58
Godzio:
A co by było gdyby d > 2r ?
8 lut 22:00
Saizou : to by trójką o bokach b,c,d nie istniał

8 lut 22:03
Saizou : w sumie o bokach r,r,d

8 lut 22:03
Godzio:
A taki trójkąt musi istnieć ?
8 lut 22:05
Saizou : jak dla mnie musi

8 lut 22:06
Godzio:
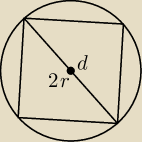
(lekko skrzywiony kwadrat bo nie chciał mi się wpisać ładnie

)
Tutaj istnieje taki trójkąt

?
8 lut 22:08
Saizou : a no nie ma

8 lut 22:09
Godzio:
Właśnie, no dobra, to w takim razie co z tym "d > 2r" (albo d ≤ 2r) ?
Da się to jakoś wytłumaczyć ?
8 lut 22:10
Ajtek:
A pisałem że P>0

.
8 lut 22:12
Saizou : gdyby d>2r to by nie mieściło się w okręgu, a skoro to przekątna trapezu wpisanego w okrąg to
mielibyśmy sprzeczność
8 lut 22:12
Godzio:

no i doszedłeś do pełnego rozwiązania, brawo

8 lut 22:14
Saizou : cześć obliczeniowa była łatwiejsza

8 lut 22:15
Eta:


8 lut 22:17
Godzio:
Obliczenia zawsze są łatwiejsze, a uzasadnienia trudniejsze, tak to już jest z tą matematyką

8 lut 22:17
Saizou : to przeliczę jeszcze zadanie 1
8 lut 22:23
Godzio:
Chyba 2

8 lut 22:23
Saizou : właśnie o to mi chodziło xd
8 lut 22:24
Saizou : | | 1−√13 | | 1 | |
m∊< |
| : |
| >  |
| | 4 | | 5 | |
8 lut 22:31
5-latek: Ajtek ale sinus 72 stopni mozna policzyc prosciej
Jesli a
n oznacza bok wielokata foremnego n wpisanego w kolo jednostkowe to latwo obliczyc
wartosci funkcji trygonometrycznch kata pi/n Jezeli przyjmiemy za ramie poczatkowe kata
promien dzielacy na polowy bok n−kata foremnego wpisanego w kolo o promieniu 1 czyli R=1 to
| | pi | | an | | pi | | an2 | |
wtedy sin |
| = |
| a cos |
| = apotema ln= √1− |
| |
| | n | | 2 | | n | | 4 | |
| | √5−1 | | 1 | | 5+√5 | |
dla n=10 mamy a10= |
| i l10= |
| √ |
| |
| | 2 | | 2 | | 2 | |
| | pi | | √5−1 | | pi | | 1 | | 5+√5 | |
to sin |
| =18= |
| cos |
| = |
| √ |
| |
| | 10 | | 4 | | 10 | | 2 | | 2 | |
Teraz tylko wzor na sin(x−y) i mamy sin(90−18) i to wystarczy tylko policzyc

8 lut 22:33
8 lut 22:33
Godzio: 

8 lut 22:34
Saizou : a dla 3 zadania mamy już warunki

8 lut 22:39
Saizou : Godzio masz coś jeszcze pod ręką ?
8 lut 22:45
Godzio:
Mam i myślę czy chcesz czy nie

Chciałbyś się trochę pogłowić (jest dużo liczenia) ?
8 lut 22:49
Saizou : zawsze można spróbować

8 lut 22:51
8 lut 22:53
Godzio:
Zadanie 4
Podstawą czworościanu ABCD jest trójkąt prostokątny ABC o kącie ostrym α i promieniu okręgu
wpisanego r. Spodek wysokości opuszczonej z wierzchołka D leży w punkcie przecięcia się
dwusiecznych trójkąta ABC, a ściany boczne wychodzące z wierzchołka kąta prostego podstawy
tworzą kąt β. Obliczyć objętość ostrosłupa.
8 lut 22:53
Saizou :
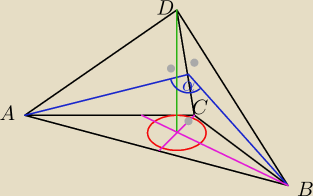
rysunek jest dobry ?
8 lut 23:05
Godzio:
Ten kąt α to powinien być β (α to kąt ostry trójkąta w podstawie)
8 lut 23:12
Saizou : oczywiście tam gdzie α miało być β

8 lut 23:12
Saizou : | | 2r2sin2α | |
mam pole podstawy P= |
| |
| | (sinα+cosα−1)2 | |
8 lut 23:28
Godzio:
Obawiam się, że pole podstawy ma jakiś błąd.
8 lut 23:46
Godzio:
Pole w najprostszej postaci. Nie pisałem wszystkiego, pewne rzeczy pisałem w pamięci.
| | sinα + cosα − 1 | |
a |
| = 2r |
| | sinα | |
| | 2rsinα | |
a = |
| |
| | sinα + cosα − 1 | |
| | 2rcosα | |
b = |
| |
| | sinα + cosα − 1 | |
| | 2r2sinαcosα | | r2sinαcosα | |
P = |
| = |
| = |
| | (sinα + cosα − 1)2 | | (1 − sinα)(1 − cosα) | |
| | | | α | | α | | r2sinα(cos2 |
| − sin2 |
| ) | | | 2 | | 2 | |
| |
= |
| = |
| | | | α | | α | | α | | (sin |
| − cos |
| )2 * 2sin2 |
| | | | 2 | | 2 | | 2 | |
| |
| | | | α | | α | | α | | r2cos |
| (cos |
| + sin |
| ) | | | 2 | | 2 | | 2 | |
| |
= |
| = |
| | | | α | | α | | α | | (sin |
| − cos |
| ) * sin |
| | | | 2 | | 2 | | 2 | |
| |
| | r2(1 + sinα) | | α | |
= |
| * ctg |
| |
| | cosα | | 2 | |
Licząc końcówkę uwzględnij to pole, albo po prostu podaj wysokość ile wyszła, żeby można było
sprawdzić wynik z odpowiedzią, bo osobiście liczyłem to zadanie kiedyś, ale nawet nie wiem czy
mam rozwiązanie

9 lut 00:00
Saizou: dzisiaj to policze ale jak sie wyspie, a terez lece, takze do dzis
9 lut 00:05
Godzio:
Do dziś

9 lut 00:13
Godzio: I jak tam

?
9 lut 22:56
Saizou : właśnie ni jak, nie mam pomysłu

9 lut 22:58
Godzio: Dam zaraz jakieś wskazówki, ale chwilkę mi to zajmie, bo chce rysunki porobić

9 lut 23:02
Saizou : spoko, mam nadzieję że nie zabraknie mi zeszytu

9 lut 23:03
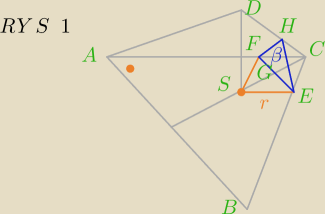
Godzio:
9 lut 23:15
Godzio:
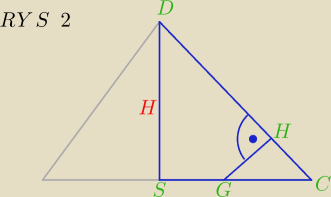
Dobra, to pora na wskazówkę.
Wsk. Znajdź trójkąty podobne (jeden z nich to oczywiście trójkąt SCD bo z niego chcesz
wysokość). Uzasadnij dlaczego są podobne.
9 lut 23:15
Godzio:
Na RYS 1 kropka powinna być przy C oczywiście

(nie wiem dlaczego tam mi się nacisnęło)

9 lut 23:15
Saizou :
Godzio szczerze ci powiem ze dzisiaj nie chce mi się myśleć

9 lut 23:21
Godzio:
Nie ma sprawy

Może kiedy indziej

9 lut 23:26
9 lut 23:26
Godzio:
Nie. r
√2 jest dobrze

9 lut 23:27
Godzio:
Najpierw ustal, które trójkąty są podobne.
9 lut 23:29
Saizou :
jak to

CS=r
√2
9 lut 23:31
Saizou : chyba już wiem
CS=r√2+r
9 lut 23:32
9 lut 23:35
Godzio:
Ok

|CS| = r
√2 (bez + r)
9 lut 23:38
Saizou : tylko gdzie jest błąd w takim razie?
9 lut 23:40
Godzio:
Hmmm, ale teraz się zastanawiam, czy jest to poprawne (chodzi o CG, czy to musi być połowa
przekątnej ?)
9 lut 23:41
Godzio:
Muszę się chwilę zastanowić

9 lut 23:45
Saizou :
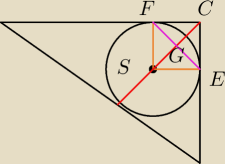
tak by raczej było

9 lut 23:47
Godzio:
No dobra, już widzę
| |DS| | | |GH| | |
| = |
| (a nie |CG| !) |
| |CS| | | |HC| | |
9 lut 23:47
9 lut 23:55
Saizou : i wystarczy policzyć objętność
| | 1 | | | | 2r2sinαcosα | |
V= |
| r√2 |
| * |
| |
| | 3 | | | | (sinα+cosα−1)2 | |
10 lut 00:06
Godzio:
| | β | |
Ok, można było trochę uprościć z tym ctg2 |
| |
| | 2 | |
Zadanie całkiem trudne

10 lut 00:22
Saizou : a no bardzo ciekawe
10 lut 09:21
 ?
?
 nawet te proste są dla mnie ciężkie co dopiero te "ciekawsze"
nawet te proste są dla mnie ciężkie co dopiero te "ciekawsze"
 Poziom też prosiłbym
maturalny
Poziom też prosiłbym
maturalny 

 .
.
 .
.

 .
.

 A o jakim założeniu mówisz ? I chodzi Ci o m (a nie o x
A o jakim założeniu mówisz ? I chodzi Ci o m (a nie o x  ) tak ?
) tak ?




 )
)
 ?
?
 . Zanim wpadłem na pomysł....
. Zanim wpadłem na pomysł....

 . To pomysł jest trudny, a nie
zadanie
. To pomysł jest trudny, a nie
zadanie 

 ?
?





 Wygrałem?
Wygrałem? 
 P(A)=Godzio=1
P(A)=Godzio=1 




 (lekko skrzywiony kwadrat bo nie chciał mi się wpisać ładnie
(lekko skrzywiony kwadrat bo nie chciał mi się wpisać ładnie  )
Tutaj istnieje taki trójkąt
)
Tutaj istnieje taki trójkąt  ?
?

 .
.
 no i doszedłeś do pełnego rozwiązania, brawo
no i doszedłeś do pełnego rozwiązania, brawo 










 Chciałbyś się trochę pogłowić (jest dużo liczenia) ?
Chciałbyś się trochę pogłowić (jest dużo liczenia) ?


 rysunek jest dobry ?
rysunek jest dobry ?



 ?
?





 (nie wiem dlaczego tam mi się nacisnęło)
(nie wiem dlaczego tam mi się nacisnęło) 

 Może kiedy indziej
Może kiedy indziej 



 |CS| = r√2 (bez + r)
|CS| = r√2 (bez + r)

 tak by raczej było
tak by raczej było 


