Marcin:
Pani Milu, też poproszę

(tamten temat jest już zbyt zagmatwany).
2 lut 17:44
5-latek: Jesli moge to prosze .
Podsatwa graniastoslupa prostego jestrapez rownoramienny w ktorym dane sa podstawy 56 i 16cm
. . Ramie trapezu jest rowne wysokosci graniastoslupa. . Oblicz pole powierzchni bocznej
graniastoslupa .
POzdrowienia dla
Mili 

2 lut 17:52
5-latek: Przepraszam ale przeoczylem . Dana jest jeszcze przekatna trapezu o dlugosci 39cm
2 lut 17:53
Mila:
Po rozwiązaniu zadania od
5−latka napisze.
Dzięki za pozdrowienia. Też pozdrawiam.

2 lut 18:00
Marcin: Nie odświeżyłem strony i tak patrzyłem na to co sobie napisałem na kartce i nie miałem pojęcia
jak się za to wziąć

Pb=3050, mam rację?
2 lut 18:10
5-latek: tak. Zgadza sie

Teraz aczekaj na zadania od
Mili 
2 lut 18:14
Marcin: Czeeekam

2 lut 18:15
Mila:
Ostrosłupy.
1) Oblicz objętość i pole powierzchni czworościanu foremnego o krawędzi a.
(Rysunek ,oznaczenia, będzie ciąg dalszy problemów)
2 lut 18:16
Marcin: Przykro mi. Próbowałem tutaj rysować, ale jakoś nie potrafię. Nie bardzo rozumiem co mam tutaj
wyliczać.
Pc =a
2√3
2 lut 18:19
zawodus: Wzór ogólnie znany, ale jakbyś miał go udowodnić?
2 lut 18:22
Marcin: Mimo że nie bardzo wiem jak zacząć w ogóle dowód tego wzoru, to mam pewność że takiego zadania
nigdzie nie dostanę, bo ten wzór jest w tablicach. Ale w sumie to jest ciekawe i bardzo
chętnie dowiem się jak go wyprowadzić

2 lut 18:26
Mila:

2) Oblicz promień kręgu wpisanego w czworościan foremny o krawędzi a.
3)Oblicz promień kręgu opisanego na czworościanie foremnym o krawędzi a.
4) oblicz cosinus kąta dwuściennego między sąsiednimi ścianami czworościanu.
2 lut 18:30
Piotr 10: Marcin nie ma tego wzoru w tablicach a dowód jest prosty wręcz, o ile wiesz co to jest
czworościan foremny
2 lut 18:35
Piotr 10: Czworościan formeny składa się z 4 ścian, które są trójkątami równobocznymi
2 lut 18:36
Mila:
Piotrze, w następnych zadaniach musi to obliczyć, o co mi chodziło w (1) zadaniu.
Spokojnie.
Marcin, masz rysunek i licz.
2 lut 18:39
Marcin: Okrąg wpisany:
Okrąg opisany:
2 lut 18:39
Marcin: Pomyłka.

2 lut 18:40
2 lut 18:41
Marcin: Myślałem że wam chodzi o udowodnienie wzoru na pole trójkąta równobocznego. Ten na czworościan
wydawał mi się oczywisty.
2 lut 18:44
Piotr 10: | | 1 | | √3 | |
a to też łatwo P= |
| a*a*sin600=a2 |
| |
| | 2 | | 4 | |
2 lut 18:45
Marcin: Jeżeli chodzi o ten kąt, to mam mały problem. Mam dwa boki trójkąta równoramiennego gdzie
jeden. Wiem że mam obliczyć kąt pomiędzy nimi, ale brakuje mi tego boku na przeciwko kąta.
Mogę dostać jakąś podpowiedź?
2 lut 18:54
Marcin: Jeżeli chodzi o ten kąt, to mam mały problem. Mam dwa boki trójkąta równoramiennego. Wiem że
mam obliczyć kąt pomiędzy nimi, ale brakuje mi tego boku na przeciwko kąta.
Mogę dostać jakąś podpowiedź?*
2 lut 18:56
Marcin: Jest tam kto?

2 lut 19:06
zawodus: oznacz sobie go jako a
2 lut 19:08
Mila:
Marcin pojechałeś wzorami z tablic, nie jestem zadowolona, ale...niech będzie.
a) wyprowadź wzór na wysokość tego czworościanu
b) szukany kąt to może byc np.∡AES=β
2 lut 19:13
Marcin: Już oznaczyłem tak jak podpowiedział zawodus, mimo że a to moja krawędź, a nie pasowała mi
tutaj.
| | 3a2 | | 3a2 | | 3a2 | |
a2= |
| + |
| −2* |
| cosx |
| | 4 | | 4 | | 4 | |
| | 3a2 | | 3a2 | | 6a2 | |
a2= |
| + |
| − |
| cosx |
| | 4 | | 4 | | 4 | |
| | 6a2 | | 6a2 | |
a2= |
| − |
| cosx / *4 |
| | 4 | | 4 | |
4a
2=6a
2−6a
2cosx
−2a
2=−6a
2cosx / /−6a
a
2 lut 19:21
Mila:
To teraz (a) proszę i jeszcze tgx.
2 lut 19:27
Saizou : a ja poproszę o dokończenie moich zadań

2 lut 19:28
Marcin: Uwaga.. wyprowadzam wzór :x
| | √24a | | 2√6a | | a√6 | |
h= |
| ⇒ |
| ⇒ |
| |
| | 6 | | 6 | | 3 | |
2 lut 19:30
Marcin: Saizou w tamtym temacie jest straszne zamieszanie, ale nie martw się. Przyjdzie czas i na nie.

2 lut 19:31
Saizou : też tak mówiłem....

2 lut 19:31
Marcin: Dobrze wyprowadziłem ten wzór?
2 lut 19:33
Marcin: tgx? tutaj nie mogę korzystać z jedynki trygonometrycznej i innych wzorów, tak?
2 lut 19:38
Mila:
Dobrze, napisałam komentarz i nie wysłałam.
Oblicz dowolnym sposobem.
2 lut 20:17
Marcin: tg=2√2?
2 lut 20:21
Mila:
tg α=2√2
Dobrze.
2 lut 20:25
Marcin: yee, cieszę się jak dziecko

2 lut 20:26
Mila:
5) W ostrosłupie prawidłowym trójkątnym dany jest kąt α nachylenia ściany bocznej do
płaszczyzny
podstawy. oblicz kąt nachylenia krawędzi bocznej do płaszczyzny podstawy.
2 lut 20:28
Marcin: | | 1 | |
Wyszło mi, że ten kąt = |
| tgx, nie mam pojęcia czy o to chodziło  |
| | 3 | |
2 lut 20:36
Mila:
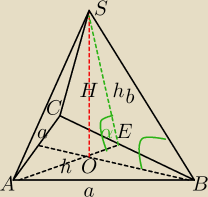
Teraz zapisz pełne obliczenia, jak na egzaminie.
2 lut 20:48
Marcin: | a√3 | | 1 | |
| To |
| wysokości trójkąta. |
| 6 | | 3 | |
| a√3 | | 2 | |
| To |
| wysokości trójkąta |
| 3 | | 3 | |
| | | | a√3 | | 3 | | 1 | | 1 | |
tgα= |
| ⇒ |
| *tgx* |
| ⇒ |
| *tgx*3 ⇒ |
| tgx |
| | | | 6 | | a√3 | | 6 | | 3 | |
2 lut 20:57
Marcin: Poprawiam się, chociaż wynik i tak pewnie jest błędny
2 lut 20:58
Bogdan:
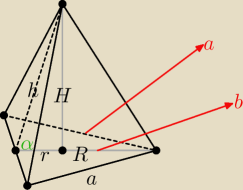
krawędź a jest niewidoczna, rysujemy przerywaną linią, linię b dla lepszego zobaczenia
problemu w zadaniu lepiej jest rysować poziomo. Staramy sie rysować bryłę w taki sposób,
żeby jak najwięcej krawędzi było widocznych.
| | 1 | | 1 | |
R = |
| a√3 = 2r, r = U{1}[6}a√3 = |
| R |
| | 3 | | 2 | |
2 lut 21:01
2 lut 21:01
Marcin: Panie Bogdanie, przecież ja w swoim poście napisałem to samo

Chyba że się mylę..
2 lut 21:03
Bogdan:
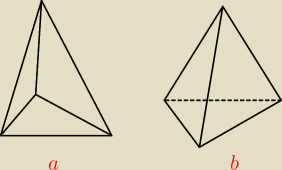
Powinno się raczej rysować ostrosłup tak jak na rysunku b.
2 lut 21:05
Bogdan:
Odnoszę się teraz tylko do rysunków, nie do zadań
2 lut 21:06
Marcin: Zawsze miałem problemy z rysowaniem brył, przyznam szczerze. Zawsze jakieś krawędzie mi
uciekały czy coś. Dziękuję za sugestię, przyda się na pewno

2 lut 21:06
Bogdan:
Kiedyś uczniowie uczyli się w szkole rysunków, w tym poprawnego rysowania brył.
Szkoda, że tej umiejętności nie naucza się teraz.
2 lut 21:09
Marcin: Teraz to w ogóle jest masakra z poziomem nauczania matematyki, przynajmniej u mnie w technikum.
Ja mam 2 lekcje matematyki w tygodniu, na których i tak w sumie nic ciekawego nie robimy.
2 lut 21:11
2 lut 21:16
Mila:
Marcin masz obliczyć kąt x w zależności od kąta α.
2 lut 21:25
Marcin: | | a√3 | |
Nie bardzo rozumiem. Czyli jak mam wyznaczyć wysokość? nie będzie ona równa |
| tgα? |
| | 3 | |
2 lut 21:34
Mila:
Masz dac wynik:
tg(x)=....
2 lut 21:40
Marcin: | | 1 | |
tgα= |
| tgx, to nie jest wynik? U Bezendu widziałem takie rozwiązanie  |
| | 2 | |
2 lut 21:42
2 lut 21:47
Marcin: Ale przecież ja mam taką odpowiedź. To że u mnie jest x zamiast β nic chyba nie zmienia.
2 lut 21:48
Mila:
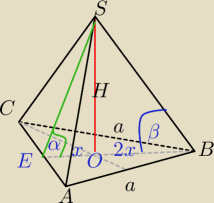
5) W ostrosłupie prawidłowym trójkątnym dany jest kąt α nachylenia ściany bocznej do
płaszczyzny podstawy. oblicz kąt nachylenia krawędzi bocznej do płaszczyzny podstawy.
EO: OB=1:2
|EO|=x
|OB|=2x, x wspólna miara
⇔
H=x*tgα
H=2x*tgβ⇔2x*tgβ=tgα⇔
2 lut 21:50
Bogdan:

2 lut 21:52
Marcin: | | a√3 | |
Przecież ja to tak zrobiłem  Tyle że za x podstawiłem |
| , co daje i tak w gruncie |
| | 6 | |
rzeczy to samo

Nadal nie rozumiem co mam źle w wyniku

2 lut 21:53
Mila:
| | 1 | |
To masz kolizję oznaczeń, poza tym masz tgα= |
| tgβ |
| | 2 | |
a to oznacza :
tgβ=2tgα
2 lut 22:05
Marcin: Kąt nachylenia do ściany bocznej nazwałem X (dla mnie tgx), a kąt nachylenia krawędzi bocznej
nazwałem α (tgα). Proszę popatrzeć na post z 20;57

Czyli jakby nie było wszystko mam
dobrze, ale mam inaczej oznaczone kąty. Dla mnie ważne jest, że obliczenia mam ok. Pozdrawiam
i liczę na kolejne zadania

2 lut 22:11
Bogdan:
Kolejne zadanie.
Wyznaczyć zależność między miarą kąta nachylenia ściany bocznej dowolnego ostrosłupa
do płaszczyzny podstawy i miarą kąta β nachylenia krawędzi bocznej do płaszczyzny
podstawy tego ostrosłupa.
2 lut 22:22
Mila:
20:48 dałam rysunek z oznaczeniami i sprawdzam wg tego. No wyjaśnione.
Jeśli chcesz uzyskac pomoc, to pisz obliczenia wg oznaczeń na rysunku, albo zapisuj dokladnie.
2 lut 22:23
Marcin: Obliczenia zrobiłem szybciej, bez tego rysunku, przez to to całe zamieszanie z wynikiem. Bardzo
przepraszam

2 lut 22:25
Marcin: Panie Bogdanie mam pytanie: Przed chwilą wyliczyłem taką zależność w ostrosłupie. Czy będzie
ona taka sama dla dowolnego ostrosłupa?
Czy kompletnie źle myślę?

2 lut 22:29
Bogdan:
Sprawdź sam
2 lut 22:31
Bogdan:
ale muszę uszczegółowić polecenie − ostrosłup jest prawidłowy, w podstawie jest wielokąt
o n wierzcholkach
2 lut 22:33
Marcin: Jeżeli w podstawie jest kwadrat, to wychodzi
2 lut 22:40
Bogdan:
Przyjmij, że podstawą jest n−kąt foremny
2 lut 22:44
Marcin: Nie bardzo wiem jak to zapisać, bo ten stosunek zależność zmienia się z zależności od podstawy.
np dla sześciokąta tgβ=tgα itd.. Jakaś wskazówka? Bo przyjęcie że podstawką jest n−kąt foremny
mi tylko utrudniło sprawę.
2 lut 22:50
Bogdan:
Nie mówiłem, że będzie łatwo

. Na razie szukaj sam rozwiązania.
2 lut 22:51
Marcin: | | 1 | | √2 | | 2 | |
Zauważyłem, że te stosunki będą wyglądać tak |
| , |
| , x, |
| Może to tworzy |
| | 2 | | 2 | | 2 | |
jakiś ciąg?

2 lut 22:59
Bogdan:
Szukaj uparcie dalej, aż do skutku − i to samodzielnie, bez oczekiwania na potwierdzenie lub
zaprzeczenie Twoim domysłom.
To jest dobra metoda na uzyskanie pełnej satysfakcji z samodzielnego rozwiązania problemu
i sprawności swojego umysłu

2 lut 23:05
Marcin: Panie Bogdanie. Co do wyników tego zadania, to muszę ze smutkiem potwierdzić swoją porażkę

4 lut 18:49
 (tamten temat jest już zbyt zagmatwany).
(tamten temat jest już zbyt zagmatwany).



 Pb=3050, mam rację?
Pb=3050, mam rację?
 Teraz aczekaj na zadania od Mili
Teraz aczekaj na zadania od Mili 


 2) Oblicz promień kręgu wpisanego w czworościan foremny o krawędzi a.
3)Oblicz promień kręgu opisanego na czworościanie foremnym o krawędzi a.
4) oblicz cosinus kąta dwuściennego między sąsiednimi ścianami czworościanu.
2) Oblicz promień kręgu wpisanego w czworościan foremny o krawędzi a.
3)Oblicz promień kręgu opisanego na czworościanie foremnym o krawędzi a.
4) oblicz cosinus kąta dwuściennego między sąsiednimi ścianami czworościanu.







 Teraz zapisz pełne obliczenia, jak na egzaminie.
Teraz zapisz pełne obliczenia, jak na egzaminie.
 krawędź a jest niewidoczna, rysujemy przerywaną linią, linię b dla lepszego zobaczenia
problemu w zadaniu lepiej jest rysować poziomo. Staramy sie rysować bryłę w taki sposób,
żeby jak najwięcej krawędzi było widocznych.
krawędź a jest niewidoczna, rysujemy przerywaną linią, linię b dla lepszego zobaczenia
problemu w zadaniu lepiej jest rysować poziomo. Staramy sie rysować bryłę w taki sposób,
żeby jak najwięcej krawędzi było widocznych.
 Chyba że się mylę..
Chyba że się mylę..
 Powinno się raczej rysować ostrosłup tak jak na rysunku b.
Powinno się raczej rysować ostrosłup tak jak na rysunku b.

 https://matematykaszkolna.pl/forum/235018.html
https://matematykaszkolna.pl/forum/235018.html

 5) W ostrosłupie prawidłowym trójkątnym dany jest kąt α nachylenia ściany bocznej do
płaszczyzny podstawy. oblicz kąt nachylenia krawędzi bocznej do płaszczyzny podstawy.
EO: OB=1:2
|EO|=x
|OB|=2x, x wspólna miara
5) W ostrosłupie prawidłowym trójkątnym dany jest kąt α nachylenia ściany bocznej do
płaszczyzny podstawy. oblicz kąt nachylenia krawędzi bocznej do płaszczyzny podstawy.
EO: OB=1:2
|EO|=x
|OB|=2x, x wspólna miara

 Tyle że za x podstawiłem
Tyle że za x podstawiłem  Nadal nie rozumiem co mam źle w wyniku
Nadal nie rozumiem co mam źle w wyniku 
 Czyli jakby nie było wszystko mam
dobrze, ale mam inaczej oznaczone kąty. Dla mnie ważne jest, że obliczenia mam ok. Pozdrawiam
i liczę na kolejne zadania
Czyli jakby nie było wszystko mam
dobrze, ale mam inaczej oznaczone kąty. Dla mnie ważne jest, że obliczenia mam ok. Pozdrawiam
i liczę na kolejne zadania 


 . Na razie szukaj sam rozwiązania.
. Na razie szukaj sam rozwiązania.


