Bryły.

Bryły. bezendu: Bryły cd.

2 lut 17:36

Mila: 1) Oblicz objętość graniastosłupa prawidłowego trójkatnego, w którym długość krawędzi podstawy jest równa 20 cm oraz kąt nachylenia przekątnej ściany bocznej do sąsiedniej ściany ma miarę 45^o.

2 lut 17:39

ja:

	1000√3
czy wynik to
	3

2 lut 17:47

ja: znaczy się

1000√6

3

2 lut 17:47

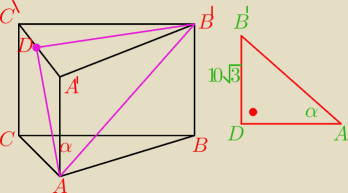
bezendu: rysunek

	20²√3
P_p=
	4

P_p=100√3 cm² α=45⁰ |DB'|=U{20√3}[2}=10√3 sin45⁰

√2		10√3
	=
2		\|AB'\|

√2|AB'|=20√3 |AB'|=10√6cm |BB'|²=(10√6)²−(20)² |BB'|²=1000 |BB'|=10√10cm V=100√3*10√10 V=1000√30cm³

2 lut 17:59

zawodus: Ile jest (10√6)²−(20)²?

2 lut 18:00

bezendu: |BB'|²=200 |BB'|=10√2 V=100√3*10√2 V=1000√6cm³

2 lut 18:03

zawodus: Teraz jest ok. Mila mam nadzieję, że nie masz mi za złe za sprawdzenie emotka

2 lut 18:05

Mila: Popraw, co wskazał zawodus.

2 lut 18:07

bezendu: To proszę kolejne, bo i tak ferie więc trzeba bryły opanować emotka

2 lut 18:07

bezendu: Poprawiłem już.

2 lut 18:07

Mila: Zawodus, wszystko w porządku. Bezendu robi postępy, coraz więcej "widzi." Zadanie 2) Oblicz objętość i pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego, mając daną jego wysokość H=20 cm oraz kąt nachylenia przekątnej graniastosłupa do płaszczyzny podstawy α=30^o.

2 lut 18:13

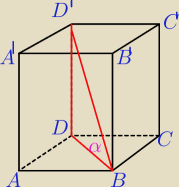
bezendu: rysunek

	1
sin30⁰=
	2

1		20
	=
2		BD'\|

|BD'|=40 |BD|²=40²−20² |BD|²=1200 |BD|=20√3 a√2=20√3

	20√6
a=		=10√6
	2

P_p=(10√6)² P_p=600cm² V=20*600=12000cm³ P_c=2P_p+4p_b P_c=2*600+4*10√6*20 P_c=1200+800√6 P_c=400(3+2√6)cm²

2 lut 18:27

52: Też mi tyle wyszło emotka

2 lut 18:29

zawodus: ok

2 lut 18:30

Mila:

Ostrosłupy. 1) W ostrosłupie prawidłowym czworokątnym o polu podstawy 36 cm², kąt nachylenia krwędzi bocznej do płaszczyzny podstawy jest równy 60^o. oblicz V i P_b tego ostrosłupa .

2 lut 18:37

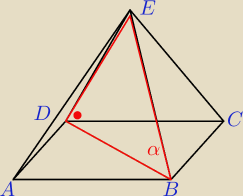
bezendu: rysunek

|DB|=6√2

	1
cos60⁰=
	2

1		6√2
	=
2		\|BE\|

|BE|=12√2 h−wysokość ściany bocznej h=3√31 P_b=4*0,5*6*3√31 P_b=36√31 P_c=36(1+√31)cm² Ale jak policzyć H ?

2 lut 18:48

zawodus: Z trójkąta DBE.

2 lut 18:51

bezendu: A te obliczenia są ok ?

2 lut 18:52

52:

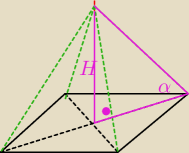
Teraz działaj

2 lut 18:52

Eta:

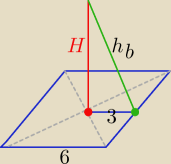
2 lut 18:53

52: I mi wyszło V=108√6 P_b=36√7

2 lut 18:53

Mila:

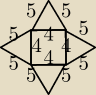
Widziałeś ostrosłup? Gdzie tam masz kąt prosty. Już proszę wyciąć siatkę z kartki i pozaginać. 1) a=6 cm

2 lut 18:55

bezendu: Zaraz poprawiam.

2 lut 19:01

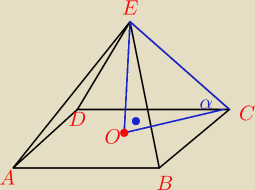
bezendu: rysunek

|OC|=3√2

	1
cos60⁰=
	2

1		3√2
	=
2		\|CE\|

|CE|=6√2 H=|OE|=3√2

	1
V=		3√236=36√2cm³
	3

P_b=4*3√7*6*0,5 P_b=36√7cm²

2 lut 19:17

52: H≠3√2

2 lut 19:20

bezendu: To już nie wiem gdzie mam błąd ?

2 lut 19:25

52:

	H
No to masz sin α=
	x

	√3
sin 60=
	2

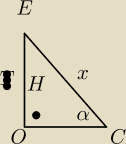
x=6√2 H=?

2 lut 19:29

Mila: POlicz tgα. Za takie zapisy nie dostaniesz pełnej puli punktów, H=3√6 skąd to 3√7?

2 lut 19:33

bezendu: 3√7 taka mi wyszła wysokość trójkąta EBC

2 lut 19:34

bezendu:

	1
V=		3√636=36√6
	3

2 lut 19:41

Mila: Dobrze. 2) Kąt dwuścienny przy podstawie ostrosłupa prawidłowego czworokątnego jest równy 60^o. Krawędź podstawy jest równa 2cm .Oblicz objętość i pole powierzchni całkowitej ostrosłupa.

2 lut 20:09

Marcin: Pani Milu, mogłaby Pani sprawdzić moje wyprowadzenie wzoru i podpowiedzieć co do tego tgx? emotka

2 lut 20:10

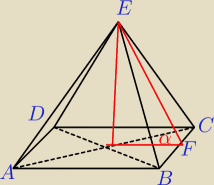
bezendu: rysunek

Czy chodzi o ten kąt ?

2 lut 20:15

Mila: Dobrze,Bezendu.

2 lut 20:18

Mila: 3)W ostrosłupie prawidłowym trójkątnym dany jest kąt α nachylenia ściany bocznej do płaszczyzny podstawy. oblicz kąt nachylenia krawędzi bocznej do płaszczyzny podstawy.

2 lut 20:29

bezendu: |OF|=1

	√3
ctg60⁰=
	3

√3		\|OF\|
	=
3		\|OE\|

√3		1
	=
3		\|OE\|

√3|OE|=3 |OE|=√3 |EF|=2 P_p=4cm²

	1		4√3
V=		4√3=		cm³
	3		3

P_c=12cm²

2 lut 20:33

bezendu: Czy mogę prosić rysunek do 3 ? Nie wiem jak zaznaczyć ten kąt nachylenia ściany bocznej ? Wiem, że musi być do przekątnej podstawy. ?

2 lut 20:36

Marcin: Bezendu widzę że dostaliśmy to samo zadanie emotka

2 lut 20:43

bezendu: Też, zauważyłem. Ale ja nie patrzę na Twoje rozwiązanie.

2 lut 20:45

Marcin: Nie dodałem żadnego rozwiązania, tylko sam wynik, który i tak jest zapewne nie taki jak powinien emotka

Zdajesz rozszerzenie, nie?

2 lut 20:46

bezendu: A jak myślisz ? emotka

2 lut 20:48

Marcin: Pytanie retoryczne

2 lut 20:48

Marcin: Jak oceniasz swoje szanse?

2 lut 20:49

bezendu: Odpowiedź znasz emotka

2 lut 20:49

bezendu: Zobaczymy w maju. Nic nie ocenią bo jeszcze wiele przede mną, mam ferie uzupełnię wiadomości to będzie ok, a raczej być powinno.

2 lut 20:50

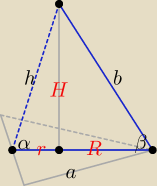
Bogdan: rysunek

Do zadania 3. α − kąt nachylenia ściany bocznej do płaszczyzny podstawy, β − kąt nachylenia krawędzi bocznej do płaszczyzny podstawy,

	1
R =		a√3 = 2r,
	3

	1		1
r =		a√3 =		R
	6		2

2 lut 20:52

Mila:

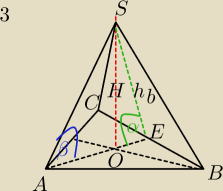
Zadanie2 dobrze. Zapisy lepsze niż były wcześniej.

2 lut 20:53

bezendu: Dziękuję Bogdan zapamiętam te własności.

2 lut 20:55

bezendu:

	\|OE\|
ctgα=		/ *H
	H

Hctgα=|OE|

	OE
H=
	ctgα

	OA
ctgβ=		/*H
	H

ctgβH=|OA|

OE		OA
	=
ctgα		ctgβ

Coś takiego ?

2 lut 21:02

Mila: Dalej skorzystaj z zależności : ozn.|AE|=h

	1
\|OE\|=		h
	3

	2
\|AO\|=		h
	3

2 lut 21:21

bezendu:

\|AE\|ctgβ		2\|AE\|ctgα
	=		/3
3		3

|AE|ctgβ=2|AE|ctgα

	2\|AE\|ctgα
ctgβ=
	\|AE\|

	2
ctgβ=
	ctgα

I dalej nie wiem ?

2 lut 21:31

Mila:

1 
h
3 

2 
h
3 

=

ctgα

ctgβ

2ctgα=ctgβ Może zostać ctgβ=2ctgα albo

2		1
	=
tgα		tgβ

stąd

	1
tgβ=		tgα
	2

2 lut 21:38

Marcin:

1
	tgx to jest odpowiedź?
2

2 lut 21:40

bezendu: Dziękuję. Na dziś już wystarczy, idę robić arkusze. emotka

2 lut 21:40

Mila:

2 lut 21:42

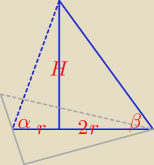
Bogdan: rysunek

a nie prościej tak?

	H		H
tgα =		i tgβ =		⇒ H = rtgα i H = 2rtgβ ⇒ rtgα = 2rtgβ / :r
	r		2r

	1
stąd tgβ =		tgα
	2

2 lut 21:46

Mila: Dla Bezendu https://matematykaszkolna.pl/forum/235153.html

2 lut 21:52