Ekstrema funkcji Mika: a)

	x2
f(x)=
	x2−9

	x2+4
b) f(x)=
	2x

Ajtek: I w czym problem?

5-latek: Pewnie w obliczeniu pochodnej

Ajtek: Tak myślisz?

Mika: bardzo bym prosiła o policzenie jednego z przykładów

Ajtek: A ja się zastanawiam, czy chodzi o ekstrema lokalne ,czy globalne .

5-latek: tak BO pozniej przyrownac do 0 to juz pikus

Ajtek: Oj czasami z przyrównaniem ułamka do 0 bywają problemy. Mika, wyznacz dziedzinę, a następnie policz pochodną.

5-latek: Mika ti wzor na pochodna ilorazu (albo iloraz pochodnej ) nigdy nie pamietam i liczysz https://matematykaszkolna.pl/strona/359.html d rugi od dolu

Ajtek: 5−latek pochodna ilorazu .

5-latek:

5-latek: Co jest Mika . dlaczego nie liczysz ? To jest proste

Ajtek: Może liczy i dlatego nie odpisuje.

5-latek: Moze podzieli sie z nami swoimi obliczeniami

Ajtek: Liczę na to.

5-latek: No to moze troche osmiele nasza kolezanke i napisze D_f=R\{−3 ,3}

5-latek: to do a)

Mika: nie mogłam wcześniej ale juz jestem no i policzyłam pochofną a co dalej?

Ajtek: Pokaż wynik pochodnej, sprawdzę czy nie ma błędu.

Mika: w A) wyszło mi −9

Mika: dobrze ?

Ajtek: Jak −9

Ajtek: Pokaż obliczenia.

Mika:

(x2)'(x2−9)−(x2)(x2−9)'		2x(x2−9)−x2(2x)		−18x
	=		=		=−9
(x2−9)'		2x		2x

Mika: nie wiem czy dobrze może jakieś błędy rachunkowe

Ajtek: O rety Dlaczego liczysz w mianowniku pochodną skoro we wzorku masz:

	f		f'*g−f*g'
(		)'=
	g		g2

Gapo .

Mika: no faktycznie xD

Ajtek: To jak wygląda pochodna?

Mika:

−18x
	coś mogę jeszcze z tym zrobić? Bo nie kogoba mi się jakos ten
x4−18x2+81

mianownik

Ajtek: Skoro się nie podoba, to go zostaw w postaci (x²−9)². Teraz sprawdzasz f'(x)=0.

Mika: czyli rozwiązuje równanie wielomianowe?

Ajtek: A po co Kiedy ułamek jest równy 0

Mika: czyli co mnoże przez to co jest w mianowniku zostaje mi −18x=0 tak?

Mika: czyli x =0 ? nie weim ja jestem tępa i tego nie umiem ... albo poprostu już o tej godzinie nie mysle

5-latek:

	A
tak. Ale zasada jest tak		=0 gdzie B≠0 bo nie wokno dzieli przez 0 ⇔ gdy A=0
	B

	0
bo		=0
	B

5-latek: Ale to sa wiadomosci z gimnazjum a Ty jestes przeciez studentka

Ajtek:

	a
Raczej nie myślisz. Tak x=0. Ułamek		=0 ⇔a=0
	b

Teraz zbadaj znaki w okolicy 0 czyli f'(x)>0 i f'(x)<0. Pamietaj że mianownik jest zawsze dodatni w tym przypadku, ponieważ masz w nim (x²−9)²

Mika: no dobrze niedziel cholero nigdy przez zero i co dalej?

Mika: skąd wiesz że studenta ?

Ajtek: 5−latek jest studentką, nadrabia zaległości i to się chwali. Jak widzisz pokazauje obliczenia .

Ajtek: W szkole średniej nie ma pochodnych, extremów lokalnych itp. w chwili obecnej .

Mika: miłomi jestem w szkole średniej w 2 liceum i mam pochodne

Mika: a przyjaciółka poszła na studniai prosiłamnie o zrobienie tych oto przykładów pochodne miałam na początku roku inie pamiętałam a wybaczcie mi prosze ale o tej godzinie człowiek juz nie myśli

5-latek: ja zawsze tak pisze zeby osmielic do dzialania

Ajtek: 2 LO I pochodne Na rozszerzeniu może faktycznie, bo miały wrócić .

Mika: tak oczywiście że są

Mika: podręcznik mogę nawet podać

Ajtek: Wracają dobre czasy w matematyce w szkole średniej, yeah .

Ajtek: To działaj zdolniacho, zawstydź koleżankę .

Mika: nie mogę nie wychodzi mi pełno błędów rachunkowych

Ajtek: f'(x)>0 ⇔ −18x>0, f'(x)<0 ⇔ −18x<0 Działasz.

Mika: to co −18x>⇔ 0 x>0 −18x<0 ⇔x<0 ? czymi sie wydaje czy to jest bez sensu

Mika: a co dalej?

Ajtek: Zastanów się gdzie zrobiłaś błędy

Ajtek: Co się dzieje ze znakiem nierówności gdy dzielimy przez liczbę ujemną

Mika: zmienia sie

Ajtek: A dlaczego nie zmieniłaś

Mika: no dobra ale to i tak wychodzi x<0 a potem x>0 ?

Ajtek: Tak. Teraz zerknij tutaj: https://matematykaszkolna.pl/strona/387.html Wszystko ładnie opisane i wyjaśnione.

Mika: no dobra to jeżeli chodzi o odpowiedz tojak mam ją napisać?

Ajtek: Zrób tabelkę i masz wszystko.

Mika:

	x2−8
jeżelichodzi o ten drugi przykład to pochodna funkcji równa się		?
	2x2

Ajtek: Nie. Pamiętaj mianownik do kwadratu, zatem (2x)². W liczniku też jest błąd.

Mika:

	2x2−8
czyli
	4x2

Ajtek: Tak, ale jak pisałem wcześniej zostawiaj mianownik w postaci (x²−9)², czyli tutaj (2x)².

Mika: a ta tabelka ma wyglądać tak samo jak w tym linku ?

Mika: no dobra

Ajtek: Dokładnie tak, pamiętając o rozwiązaniach pochodnej. Czyli f'(x)>0 i f'(x)<0 i odpowiednie przedziały .

Mika: f'(x)=0 czyli x=−2 V x=2

Mika: chodzi mi teraz o ten drugi przykład

Mika: ?

Ajtek: . Teraz sprawdzasz warunki dla obu tych liczb f'(x)>0 i f'(x)<0, oczywiście dla każdej oddzielnie.

Mika: czy dla dla f'(x)>−2 wyjdzie pierwiastek z 3

Mika: ? bo nie wiem czy dobrze licze

Mika: mogę prosić o zrobienie tego drugiego przykładnu bardzo proszę

Ajtek: Nie . Liczysz f'(−2)>0 i f'(−2)<0 i analogicznie dla 2 . −2 i 2 są podejrzane o istnienie extremum lokalnego. Należy sprawdzić, czy następuje zmiana znaku w okolicy tych punktów.

Mika: dziękuje

Ajtek: Powodzenia .

Mika: ale czy to dobrze zrobiłam

2x2−8
	>−2
(2x2)

2x²−8>−2 2x²>6 x>−√3 x>√3

Mika: w mianowniku powinno być (2x)²

Ajtek: Nie . Wyliczyłaś f'(x)=0 gdy x=−2 lub x=2 I teraz sprawdzasz: f'(x)> 0 i f'(x)<0 dla x=−2, analogicznie robisz dla x=2 .

Mika:

	1
dla x=−2 będzie
	2

Mika: dobrz czy nie?

Mika: coś źle zrobiłam

Mika: już nie myśle a przykład musze dzisiaj zrobić a w sumie to juz powinnam mieć zrobiony

Mika:

	2x2−8
powinnam do tego		>0 pod x podstwaić −2
	(2x)2

Mika: ii jak tak robie to wychodzi 0

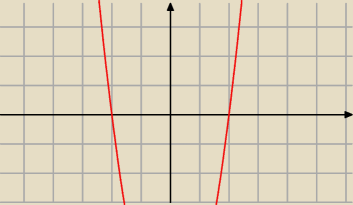
Ajtek: Pogubiłem się ja . W liczniku pochodnej masz parabolkę 2x²−8=2(x−2)(x+2) Ramiona parabolki w górę, ponieważ a=2>0 Tam gdzie wykres jest nad osią Ox czyli f'(x)>0 funkcja jest rosnąca, tam gdzie pod osią to funkcja jest malejąca. Dla x=−2 następuje zmiana znaku z + na −, zatem mamy max lokalne. Teraz prześledź to dla punktu x=2

Mika: czyli jak ja to mam zrobić bo ja już zgłupiałam

Mika: nie rozumiem

Ajtek: Najlepiej jest narysować wykres licznika i odczytać z niego wartości . Tak jak ja zrobiłem w poście wyżej.

Mika: moszesz mi proszę napisać rozwiązanie do tego 2 przykłady bardzo Cię o to rposzę bo ja tego już nie policze

Mika: jak ja z tego wykresu nic nie widze

Ajtek: Tutaj nie ma co już co liczyć. Policzyłaś że f'(x)=0 dla x=−2 lub x=2. Teraz ryzujesz sobie tą parabolkę z licznika i patrzysz jak sie zmienia wartość tej paraboli. Napisałem to w poście z godziny 23:12.

Mika: czyli jeżeli odp to co tzreba na[isac

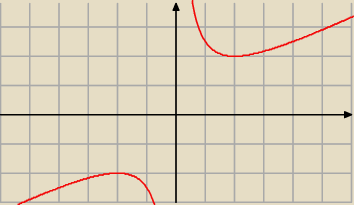
Ajtek: Dla x=−2 mamy max lokalne, dla x=2 min lokalne.

	x2+4
Na rysunku powyżej masz wykres tej funkcji: f(x)=
	2x

Mika: czyli tabelke mam rysować?

Ajtek: Tak, tylko odczytaj wartości z rysunku z godziny 23:12.