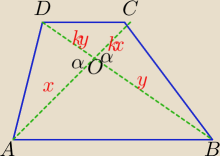
. Piotr 10: W trapezie ABCD (AB II CD) przekątne przecinają się w punkcie O. Oblicz pole trapezu wiedząc, że pole trójkąta wynosi ABO wynosi 16, zaś pole trójkata ADO wynosi 9. ΔAOB ∼ Δ DOC (cecha kkk)

	1
PΔADO=		*x*ky*sinα
	2

	1
PΔCOB=		*y*kx*sinα
	2

P_ΔADO=P_ΔCOB=9

	1		1
PΔAOB=		*x*y*sin(180−α)=		*x*y*sinα=16
	2		2

1
	*x*ky*sinα=9
2

1
	*x*y*sinα=16
2

Dzieląc stronami:

	9
k=
	16

PΔDOC
	=k2
PΔAOB

P_ΔDOC=5,0625 P_trapezu=2*9+16+5,0625=39,0625 [j²] OK?

Mila: Tak.

Piotr 10: Dziękuję

pigor: ...,a w dwóch linijkach dla leniwych myślicieli np. tak : niech x=P_ΔDCO, to ¹⁶₉=⁹_x ⇔ 16x= 9*9 ⇔ x= ⁸¹₁₆, to P_ABCD= 16+2*9+⁸¹₁₆= 34+5¹₆= 39¹₆ − szukane pole . ...

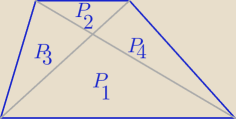Eta: P(tr)= (√P₁+√P₂)² ,

	9
gdzie P3= √P1*P2⇒ 9=4√P2⇒ √P2=
	4

	9		625		1
P(tr)= ( 4+		)2=		= 39		[j2]
	4		16		16

Eta: A pigor ...zjadł 16 w mianowniku

pigor: ... , dziękuję nieprawda, bo tylko 1−jedynkę − cyfrę dziesiątek mianownika ułamka ¹₁₆, a więc miało być 34+5¹₁₆=39¹₁₆

Eta:

Piotr 10: Eta a na maturze jakbym skorzystał ze wzorów, których użyłaś bez wyprowadzania ich to bym miał maksa za zadanie, czy by obniżyli punkty ?

Eta: Hehe .. jeżeli ja sprawdzałabym Twoją pracę , to dałabym Ci maxa, bo to mój ulubiony wzorek ( był wyprowadzany w zadaniach w I LO

Piotr 10: Fajne wzorek, szybko zadanie można nim zrobić, Dzięki

Eta: https://matematykaszkolna.pl/forum/191513.html

Eta: https://matematykaszkolna.pl/forum/133835.html