.
bezendu:
Kombinatoryka
Oblicz ile jest liczb naturalnych ośmiocyfrowych takich, że iloczyn cyfr w ich zapisie
dziesiętnym jest równy 12

21 gru 18:01
21 gru 18:05
Piotr 10: (4,3,1,1,1,1,1,1)
Cyfrę 3 mogę postawić na 8 sposobów, cyfrę 4 na 7 sposobów, reszta to 1 sposób(same jedynki)
8*7*1=56
(6,2,1,1,1,1,1,1)
Cyfrę 6 mogę postawić na 8 sposobów, cyfrę 2 na 7 sposobów, reszta to 1 sposób(same jedynki)
8*7*1=56
(2,2,3,1,1,1,1,1)
28*6*1=168
168+56+56=280
21 gru 18:17
utem:
(34111111) liczb o takich cyfrach w zapisie będzie U{8!]{6!}
liczba wszystkich permutacji podzielona przez 6!, bo jedynki są nierozróżnialne ,
(22311111) liczb o takich cyfrach w zapisie będzie U{8!]{2!5!}
(26111111) liczb o takich cyfrach w zapisie będzie U{8!]{6!}
Zliczaj.
21 gru 18:18
21 gru 18:21
Piotr 10: Ej nie możesz pisać tak
21 gru 18:28
utem:
Tam masz ułamki, a nie symbol Newtona, źle to zapisane. Nie zauważyłam . Poprawiam zapis.
| | 8! | |
(34111111) liczb o takich cyfrach w zapisie będzie |
| =56 |
| | 6! | |
liczba wszystkich permutacji podzielona przez 6!, bo jedynki są nierozróżnialne ,
| | 8! | |
(22311111) liczb o takich cyfrach w zapisie będzie |
| =168 |
| | 2!5! | |
liczba wszystkich permutacji (8!) podzielona przez 5!, bo jedynki są nierozróżnialne ,przez 2!
bo dwójki są nierozróżnialne ( powtarzają się)
| | 8! | |
(26111111) liczb o takich cyfrach w zapisie będzie |
| =56 |
| | 6! | |
21 gru 18:30
bezendu:
(34111111)= 3 może stać na 8 miejscach, 4 na siedmiu, 1−na sześciu ?
21 gru 18:34
utem:
MOżesz tak sobie wyobrazić jak pisze Piotr.
Liczby z cyframi:
(34111111)
3 stawiasz na jednym z 8 miejsc, 4 stawiasz na jednym z 7 miejsc, pozostałe miejsca zajmują
jedynki na jeden sposób ( są nierozróżnialne, jesli je przestawisz między sobą, to masz tę
samą liczbę)
Ja podaję taki sposób
Liczba z cyframi:
(34111111) wszystko mieszam , czyli na 8! sposobów przestawiłam wszystkie cyfry, ale
podzieliłam przez 6!, bo jedynki są nierozróżnialne .
liczba
(34111111) jest taka sama jak (34111111)
21 gru 18:44
bezendu:
Jednak chyba wolę drugą wersję

21 gru 18:54
bezendu:
Oblicz, ile jest liczb naturalnych trzycyfrowych podzielnych przez 6 lub podzielnych przez 15.
Zrobiłem to z ciągu arytmetycznego
a) podzielne przez 6
a1=102
r=6
an=996
102+(n−1)*6=996
102+6n−6=996
6n=900
n=150
b) podzielne przez 15
a1=105
r=15
an=990
105+(n−1)*15=990
105+15n−16=990
15n=900
n=60
60+150=210
Jak to zrobić za pomocą kombinatoryki?
21 gru 19:00
Piotr 10: źle

21 gru 19:01
Piotr 10: Teraz wypisz liczby trzycyfrowe które są podzielne zarówno przez 6 i przez 15
21 gru 19:02
bezendu:
Czemu źle ?
21 gru 19:02
Piotr 10: np 120 dzieli się przez 6 i przez 15
21 gru 19:04
bezendu:
120+(n−1)*30=990
120+30n−30=990
30n=900
n=30
n=150+60−30=180
21 gru 19:08
bezendu:
Da się to jakoś obliczyć za pomocą kombinacji ?
21 gru 19:09
Piotr 10: I teraz git

21 gru 19:09
Piotr 10: Jeśli o mnie chodzi to ja nie wiem czy da się

21 gru 19:10
bezendu: @utem ?
21 gru 19:11
bezendu: Ile jest liczb sześciocyfrowych, które mają cztery cyfry parzyste i dwie nieparzyste?
P−cyfra parzysta
N−cyfra nieparzysta
PPPPNN
21 gru 19:23
bezendu:
Ale coś mało tych liczb

21 gru 19:25
Piotr 10: I cyfra parzysta
v
I cyfra nieparzysta
Fajnie jakby ktoś to sprawdził
21 gru 19:27
bezendu: Albo podał inny sposób
21 gru 19:29
Piotr 10: A czytałeś rozwiązanie ze strony zadania.info ?
21 gru 19:33
bezendu:
Nie czytałem. Dostałem ponad 100 zadań z kombinatoryki i prawdopodobieństwa do zrobienia na
święta. A rozwiązań nie szukam na internecie

21 gru 19:35
Piotr 10: Spoko, ja też dostałem dużo arkuszy do robienia

. Około 15

. Jak chcesz, ale tam jest
wyjaśnione wszystko

21 gru 19:37
utem:
Dobrze.
203125 liczb
21 gru 19:38
bezendu:
Ale jak dojść do tego wyniku. Tam jeszcze będzie 0 (bo jest parzyste) a nie może stać na 1
miejscu ?
21 gru 19:39
utem:
Sposób Piotra jest bardzo dobry.
21 gru 19:39
Piotr 10: Dzięki
utem za sprawdzenie

21 gru 19:40
utem:
Wyjaśni Piotr? Czy Ja mam to zrobić?
21 gru 19:40
bezendu:
Wolę Twoje wyjaśnienie
utem 
21 gru 19:41
Piotr 10: Jak możesz to Ty wyjaśnij, bo ja zajęty troszkę

21 gru 19:41
utem:
(PPPPNN) taki zestaw cyfr
1)
(P−−−−−)
na pierwszym miejscu liczba parzysta− tylko na 4 sposoby( bez 0)
wybieram dwa miejsca dla liczb nieparzystych, każdą nieparzystą wybieram na 5 sposobów, na
pozostałe miejsca 3 parzyste na 5 sposobów
2) (N−−−−−)
na pierwszym miejscu liczba nieparzysta− na 5 sposobów
wybieram 1 miejsca dla liczby nieparzystej, nieparzystą wybieram na 5 sposobów, na pozostałe
miejsca 4 parzyste, każdą na 5 sposobów.
21 gru 19:49
bezendu:
| | | |
Czegoś nie rozumiem czemu 4* | ? |
| | |
21 gru 19:51
utem:
Na pierwsze miejsce mogę wybrać liczbę parzystą spośród {2,4,6,8}, czyli na 4 sposoby, na
pozostałych miejscach będą 3 parzyste i 2 nieparzyste, wybieram dwa miejsca dla nieparzystych
| | | |
: | =10, dalej wiadomo, jak wyżej napisałam |
| | |
Można też inaczej:
na pierwszym miejscu parzysta na 4 sposoby, wybieram 3 miejsca dla 3 parzystych
| |
=10 , następnie 3 parzyste na 53 sposobów, na pozostałe miejsca wejdą 2 nieparzyste na |
| |
5
2 sposobów.
Łącznie
albo
21 gru 20:41
5-latek : Juz od dluzszego czasu podejrzewalem za
utem to tak naprawde
Mila 
Pozdrawiam


21 gru 20:46
bezendu:
5−latek a ja się z Tobą zgadzam w 100%

21 gru 20:46
5-latek : bezendu Zdradzily ja tak ladnie wykokonywane rysunki

21 gru 20:49
bezendu:
Może ktoś wytłumaczyć to ?
21 gru 21:31
utem:
Czego jeszcze nie rozumiesz?
Przeczytałeś to z 20:41?
21 gru 21:34
bezendu:
Przepraszam, nie zauważyłem postu 20:41.
21 gru 21:36
utem:
Wszystko jasne?
21 gru 21:45
bezendu:
Tak, dziękuję ale mam jeszcze sporo tych zadań

21 gru 21:48
utem:
Pozdrawiam Was, Eto po przeczytaniu usuń ten post i z 21:49.
21 gru 21:50
bezendu:
Mila mam jeszcze takie
Oblicz prawdopodobieństwo tego, że w trzech rzutach symetryczną sześcienną kostką do gry suma
kwadratów liczb uzyskanych oczek będzie podzielna przez 5. (Przepraszam, że wstawiam tak
zadania bez swoich obliczeń ale nie ogarniam tego )
21 gru 21:52
utem:
Już muszę znikać, jutro wszystko wyjaśnię.
Dobranoc.

21 gru 21:54
bezendu: Dobranoc

21 gru 21:54
Eta:
No to tak

reszty z dzielenia przez
5 kwadratów liczby oczek
1
2=1 R=1
2
2=4 R=4
3
2=9 R=4
4
2=16 R=1
5
2=25 R=0
6
2=36 R=1
czyli mamy taki układ sumy kwadratów oczek podzielnej przez
5
A
1 = 0 +0+0 i A
2= 0+1+4
|A
1|= 1 bo są to oczka 5,5,5
A
2 −−− jedna 5 i jedno oczko z {1,4,6} oraz jedno oczko z {2,3}
|A
2| = 1*3*2 *3! ( bo te trójki jeszcze należy spermutować na 3!
|A|=|A
1|+|A
2| =....
|Ω|=6
3
P(A)=.........

21 gru 22:35
matyk: Bezendu pamiętaj o mnie

21 gru 22:41
bezendu:
Listonosz losowo rozmieszcza 7 listów w 5 różnych skrzynkach na listy. Oblicz
prawdopodobieństwo, że w każdej skrzynce znajdzie się przynajmniej jeden list.
Nie chcę żadnych linków ani gotowych rozwiązań. Proszę tylko powiedzieć jak zacząć.
22 gru 18:19
utem:
Poprzednie ze wskazówką Ety rozwiązałeś?
Po odpowiedzi napiszę wskazówkę do 18:19.
22 gru 18:57
bezendu:
Tak, tamto zadanie już rozwiązałem.
22 gru 19:02
cicha noc:
|Ω|= ....
rozważ dwie sytuacje:
A1 −−− w jednej z 5 skrzynek 3 listy i w pozostałych 4 skrzynkach po jednym liście
A2 −− w dwu skrzynkach z 5 skrzynek po 2 listy i w pozostałych 3 skrzynkach po jednym liście
|A|= }A1|+|A2|= ....
22 gru 19:09
bezendu:
A można jakoś inaczej to zrobić ?
22 gru 19:28
cicha noc:
Jak? Zapytaj listonosza

22 gru 19:29
bezendu:

22 gru 19:33
cicha noc:

22 gru 19:39
Saizou : można też z skorzystać z zdarzenia przeciwnego, ale będzie dłużej (chyba)
22 gru 19:40
cicha noc:
Chciałeś "tylko podpowiedź"
22 gru 19:40
bezendu:
Zadanie z arkusza Pazdro arku 5( Albo ja mam błąd w obliczeniach albo w druku )
W klasie III a jest 10 dziewcząt i 15 chłopców. Oblicz prawdopodobieństwo, że w losowo wybranej
delegacji trzyosobowej tej klasy będzie co najwyżej jedna dziewczyna
|Ω|={23*24*25}{6}=2300
| | 12!*13*14*15 | | 13!*14*15 | |
|A|= |
| + |
| *10 |
| | 12!*6 | | 13!*2 | |
| | 13*14*15 | | 14*15 | |
|A|= |
| + |
| *10 |
| | 6 | | 2 | |
|A|=455+105*10
|A|=1505
22 gru 19:47
bezendu:
Eta już zrobiłem Twoim sposobem ale pytam jeszcze o inny sposób. Wiem, że pytałem o
podpowiedź

22 gru 19:48
Saizou : pewno czeski błąd

22 gru 19:56
bezendu:
Też myślę, że błąd w druku bo już 5 razy liczyłem to zadanie

22 gru 20:02
zombi: Dobrze masz. Błąd w książce xd
22 gru 20:04
bezendu:
Kolejne do sprawdzenia:
Jest 60 pytań egzaminacyjnych. Student losuje trzy pytania. Aby zdać egzamin, trzeba
odpowiedzieć na na co najmniej dwa pytania.Student zna odpowiedzi na 40 pytań. Oblicz
prawdopodobieństwo zdarzenia A−student zda egzamin. Czy prawdopodobieństwo to jest większe od
| | 3 | |
|
| . Odpowiedź uzasadnij. |
| | 4 | |
| | | | 57!*58*59*60 | |
|Ω|= | = |
| =34220 |
| | | 57!*6 | |
| | 38!*39*40 | | 37!*38*39*40 | |
|A|= |
| *20+ |
| |
| | 2 | | 37!*6 | |
|A|=780*20+9880
|A|=25480
| | 25480 | | 1274 | |
P(A)= |
| = |
| |
| | 34220 | | 1711 | |
| | 3 | |
Prawdopodobieństwo zdania egzaminu jest mniejsze od |
| |
| | 4 | |
OK ?
22 gru 20:30
5-latek: Ale
cicha noc Eta bedzie z 24/25

22 gru 20:46
bezendu: 
22 gru 20:48
5-latek:
22 gru 20:50
bezendu: 
22 gru 21:06
utem:
Masz błędy w zapisie:(stracisz punkty na sprawdzianie)
=39*20*20=15600
| | 40! | | 37!*38*39*40 | | 38*39*40 | |
= |
| = |
| = |
| =19*13*40=9880 |
| | 3!*37! | | 6*37! | | 6 | |
| | 15600+9880 | | 1560+988 | | 2548 | | 3 | |
P(A)= |
| = |
| = |
| ≈0,7445< |
| =0,75 |
| | 58*59*10 | | 58*59 | | 3422 | | 4 | |
22 gru 21:31
utem:
I co z tymi listami?
22 gru 21:33
bezendu:
Listy już zrobiłem. Mila, sprawdzian z tego już miałem, teraz robię pracę domową na święta
a mam mnóstwo tych zadań z prawdopodobieństwa i kombinatoryki. I czemu mój zapis nie jest
poprawny ?
22 gru 21:38
bezendu:
A w zadaniu 19:47 zapis jest poprawny ?
22 gru 21:48
utem:
W trzeciej linijce masz źle |A| , popatrz uważnie.
22 gru 21:49
utem:
Ile Ci wyszło w zadaniu z listami?
22 gru 21:50
bezendu:
Brakuje 38!.
22 gru 21:51
bezendu:
| | 672 | |
Zadnie z listami |
| . |
| | 3125 | |
22 gru 21:52
utem:
Tak.
22 gru 21:52
cicha noc:
zad. z listami :

22 gru 21:53
bezendu:
A zapis zadania 19:47 ?
22 gru 21:55
bezendu: Ze zbioru liczb {1,2,3,4,5,6,7,8,9,10,11,12,13} losujemy bez zwracania 4 liczby. Oblicz jakie
jest prawdopodobieństwo, że wśród 4 otrzymanych liczb jest dokładnie jedna para liczb o sumie
równej 14.
| | | | 9!*10*11*12*13 | | 10*11*12*13 | |
Ω= | = |
| = |
| =715 |
| | | 4!*9! | | 24 | |
|A|=?
22 gru 22:02
Hajtowy: O zdarzeniach sprzyjających myślimy następująco:
*musimy wybrać jedną z powyższych par, a potem musimy dobrać jeszcze dwie liczby tak, aby nie
były z jednej pary.
Jedną parę możemy wybrać na 6 sposobów.
Po wybraniu tej pary pozostaje 13 − 2 = 11 liczb i z nich musimy wybrać jeszcze dwie.
| | | |
Dwie pozostałe liczby możemy wybrać na | = 55 sposobów. |
| | |
Od tych 55 możliwych par musimy jednak odjąć 5 par, w których suma jest równa 14. W sumie 3 i 4
liczbę możemy więc wybrać na 55 − 5 = 5 0 sposobów. Jest więc 6 * 50 = 300 zdarzeń
sprzyjających i prawdopodobieństwo jest równe:
| | 6*50 | | 60 | |
P(A)= |
| = |
| |
| | 13*11*5 | | 143 | |
22 gru 22:22
bezendu:
Hmm ?
22 gru 22:24
22 gru 22:36
bezendu: Zaraz przeanalizuję

22 gru 22:39
bezendu:
Mila masz jeszcze czas na diagramy Venna ?
22 gru 22:41
utem:
Jutro. Dobranoc

22 gru 22:44
bezendu:
Dziękuję, za poświęcony czas ! Dobranoc

22 gru 22:47
bezendu:
Zdarzenia losowe A,B zawarte są w Ω P(A∩B')=0,1 P(A'∩B)=0,2 Wykaż, że P(A∩B)≤0.7
Nie chcę żeby ktoś mi tu pisał gotowca albo podawał link.. Proszę o diagram Venna dla tego
przypadku.
23 gru 21:06
cicha noc:
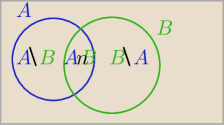
A\B=A∩B
' , B\A=A
'∩B
0≤P(AUB)≤1 i P(AUB)= P(A\B)+P(B\A)+P(A∩B)
i teraz działaj ........

23 gru 21:15
utem:
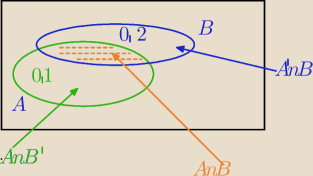
symbol n zamiast iloczynu zbiorów
23 gru 21:17
bezendu:
Z diagramu wynika, że:
A∩B'=A\B
A'∩B=B\A
A skąd wzięło się A∩B (pomarańczowe) ?
23 gru 21:20
cicha noc:
Wspólne elementy to........ część wspólna

,że tego nie wiesz !
23 gru 21:21
bezendu:
A∩B to wspólny element i to wiem, ale tam mam A'∩B i A∩B' ?
23 gru 21:26
utem:
Przecież masz tam strzałki, to co jest poza częścią wspólną, to Twoje iloczyny A∩B' i A'∩B.
23 gru 21:29
Eta:
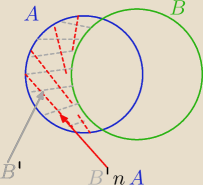
23 gru 21:29
bezendu:
P(A\B)+P(B\A)+P(A∩B)≤1 ?
23 gru 21:32
Eta:
dokładnie

tak napisałam Ci w poście
21:15
23 gru 21:34
bezendu:
Nie zauważyłem tego

23 gru 21:35
Eta:
A post
100 mi ukradłeś

23 gru 21:36
bezendu:
P(A∩B')+P(A∩B)+P(A'∩B)≤1
0,1+P(A∩B)+0,2≤1
P(A∩B)≤0,7
23 gru 21:38
Eta:

23 gru 21:39
utem:
No i pięknie, dla obojga

i wesołych świąt.
23 gru 21:53
bezendu: Rzucamy trzykrotnie symetryczną kostką sześcienną do gry. Oblicz prawdopodobieństwa
następujących zdarzeń:
A – na każdej kostce wypadnie nieparzysta liczba oczek
|Ω|=216
A={(1,1,1), (1,1,3) (1,1,5) (1,3,1) (1,3,3) (1,3,5) (1,5,5) (3,3,3) (3,3,1) (3.3.5) (3,1,3)
(3,1,1) (3,1,5) (3,5,1) (3,5,5) (5,5,5) (5,1,1) (5,3,3) (5,1,5) (5,1,3) (5,3,1) (5,5,1)
(5,3,5) (5,5,3)
|A|=24
Ale to jest błędne rozwiązanie

23 gru 21:55
bezendu:
Mila Tobie i
Ecie również życzę Wesołych Świąt

23 gru 21:56
utem:
|A|=3*3*3 wybierasz ze zbioru {1,3,5}
23 gru 21:58
bezendu:
Czyli ''zjadłem'' 3 możliwości. Czyli zbiór jest 3 elementowy czyli liczb permutacji 3! to już
wgl nie wyjdzie ?
23 gru 22:02
bezendu: ?
25 gru 19:04
bezendu: ?
25 gru 19:51
Rafał28:
Masz 3−elementowy zbiór i to są 3−wyrazowe wariacje z powtórzeniami 33.
Zapomniałeś w swoim zbiorze |A| między innymi o przypadku (1, 5, 1) i jeszcze dwóch innych.
25 gru 19:54
utem:
Przy takim doświadczeniu ( 3 rzuty kostką) w danym zdarzeniu ,
możesz wyrzucić oczka zbioru {1,3,5}
|A|=3*3*3 na pierwszej kostce na 3 sposoby, na drugiej na 3 sposoby, na trzeciej na trzy
sposoby
25 gru 19:57
bezendu:
Czyli to nie jest 3! tylko 33 ?
25 gru 19:58
BoosterXS: Dokładnie "

25 gru 20:03
BoosterXS: Oblicz prawdopodobieństwo otrzymania w rzucie dwiema nierozróżnialnymi sześciennymi kostkami do
gry:
a) jedynki na jednej z kostek,
b) nieparzystej liczby oczek na obydwu kostkach,
Ja bym liczył P(A)=1036=518 ale do odpowiedzi ni pasuje, ktoś coś może z tym
podziałać?
Odpowiedzi mam takie.
a) 521
b) 27
25 gru 23:21
bezendu:
A tak ciężko założyć nowy temat ?

Ten założyłem ja z myślą o swoich zadaniach.
25 gru 23:24
BoosterXS: Sory, nie wiedziałem, że ten temat jest "podpisany". Ale już jak je tu wrzuciłem, to może nie
beziesz miał nic przeciwko, żeby je tu rozwiązać?
25 gru 23:27
25 gru 23:30
BoosterXS: dlaczego w b) 1/4 ? a nie będzie 1/6

25 gru 23:49
zvx:
|B|=3*3
P(B)=...
25 gru 23:53
bezendu:
Takich zdarzeń masz 9 kolego

25 gru 23:58
BoosterXS: W takim razie c) nieparzystej liczby oczek na jednej kostce także będzie 9/36 ?
26 gru 00:00
26 gru 00:04
bezendu:
| | 1 | |
sorry |
| powinno być  |
| | 2 | |
26 gru 00:07
BoosterXS: Bardzo ci dziękuję utem, a czy możesz mi jeszcze wyjaśnić sprawę z |Ω|=21 dlaczego akurat tyle?
26 gru 18:11
26 gru 18:38
Mila:
Jednak odpowiedzi 23:21 nie są prawidłowe, bo zdarzenia elementarne nie są jednakowo
prawdopodobne, gdy mamy tylko 21 zdarzeń elementarnych. Wtedy trzeba inaczej liczyć.
Dobrze zaczął ( zaczęła) bezendu
26 gru 19:28
bezendu:
bezendu=On

Już tyle jestem na tym forum

26 gru 19:32
Eta:


26 gru 19:35
bezendu:
A na imię nie mogę zmienić bo już taki jest na forum, a cyferek w nicku nie lubię

26 gru 19:37
utem:

dla
bezendu, dla
Ety 

26 gru 19:38
26 gru 19:38
bezendu:
Albo z dwóch komputerów się loguję i dlatego Mila i utem ?
26 gru 19:40
Eta:
dla
Utem 
dla
bezendu 

?
26 gru 19:40
bezendu:
Dziękuję

26 gru 19:41
Eta:
No toprawdziwa "Mila" wiedziałaby,że
bezendu to grzeczny chłopczyk

26 gru 19:42
utem:
Mila ma sklerozę po świątecznych smakołykach.
26 gru 19:43
Eta:


26 gru 19:44







 . Około 15
. Około 15  . Jak chcesz, ale tam jest
wyjaśnione wszystko
. Jak chcesz, ale tam jest
wyjaśnione wszystko 



 Pozdrawiam
Pozdrawiam 






 reszty z dzielenia przez 5 kwadratów liczby oczek
12=1 R=1
22=4 R=4
32=9 R=4
42=16 R=1
52=25 R=0
62=36 R=1
czyli mamy taki układ sumy kwadratów oczek podzielnej przez 5
A1 = 0 +0+0 i A2= 0+1+4
|A1|= 1 bo są to oczka 5,5,5
A2 −−− jedna 5 i jedno oczko z {1,4,6} oraz jedno oczko z {2,3}
|A2| = 1*3*2 *3! ( bo te trójki jeszcze należy spermutować na 3!
|A|=|A1|+|A2| =....
|Ω|=63
P(A)=.........
reszty z dzielenia przez 5 kwadratów liczby oczek
12=1 R=1
22=4 R=4
32=9 R=4
42=16 R=1
52=25 R=0
62=36 R=1
czyli mamy taki układ sumy kwadratów oczek podzielnej przez 5
A1 = 0 +0+0 i A2= 0+1+4
|A1|= 1 bo są to oczka 5,5,5
A2 −−− jedna 5 i jedno oczko z {1,4,6} oraz jedno oczko z {2,3}
|A2| = 1*3*2 *3! ( bo te trójki jeszcze należy spermutować na 3!
|A|=|A1|+|A2| =....
|Ω|=63
P(A)=.........
















 A\B=A∩B' , B\A=A'∩B
0≤P(AUB)≤1 i P(AUB)= P(A\B)+P(B\A)+P(A∩B)
i teraz działaj ........
A\B=A∩B' , B\A=A'∩B
0≤P(AUB)≤1 i P(AUB)= P(A\B)+P(B\A)+P(A∩B)
i teraz działaj ........ 
 symbol n zamiast iloczynu zbiorów
symbol n zamiast iloczynu zbiorów
 ,że tego nie wiesz !
,że tego nie wiesz !

 tak napisałam Ci w poście 21:15
tak napisałam Ci w poście 21:15



 i wesołych świąt.
i wesołych świąt.



 Ten założyłem ja z myślą o swoich zadaniach.
Ten założyłem ja z myślą o swoich zadaniach.




 http://www.mf.fundacja2lo.pl/pdf2012/03_005_10_zadan.pdf Jeszcze raz dziękuję
http://www.mf.fundacja2lo.pl/pdf2012/03_005_10_zadan.pdf Jeszcze raz dziękuję 
 Już tyle jestem na tym forum
Już tyle jestem na tym forum 



 dla bezendu, dla Ety
dla bezendu, dla Ety 

 dla bezendu
dla bezendu 
 ?
?



