Doświadczenie
bezendu:
Doświadczenie wieloetapowe
W zielonym pudełku jest 10 monet pięciozłotowych i 5 monet dwuzłotowych, a w białym pudełku są
2 monety pięciozłotowe i 3 monety dwuzłotowe. Z zielonego pudełka losujemy jedną monetę i
wrzucamy do białego pudełka. Następnie z białego pudełka losujemy jednocześnie 2 monety.
Oblicz prawdopodobieństwo, że z białego pudełka wylosujemy w sumie 7 złotych ?
Może ktoś powiedzieć jak się za to zabrać, na maturze nie zrobiłem tego zadania
8 gru 17:22
Piotr 10: Za pomocą drzewka najlepiej
8 gru 17:24
Trivial: To jest zadanie odrobinę nietrywialne. Ale da się rozwalić w skończonej ilości czasu.
8 gru 17:26
bezendu:
To może ktoś pokazać to drzewko do tego przykładu ?
8 gru 17:27
8 gru 17:33
Trivial:
Moim zdaniem najłatwiej jest rozbić zadanie na dwie części.
Część pierwsza.
1. Załóżmy, że wylosowaliśmy 5 zł. P(x*2 + y*5 = 7) =
obliczyć= p
1
2. Załóżmy, że wylosowaliśmy 2 zł. P(x*2 + y*5 = 7) =
obliczyć= p
2
Część druga.
Prawdopodobieństwo spełnienia warunków zadania jest następujące:
Pozostało wyliczyć p
1, p
2.
8 gru 17:36
bezendu:
Spróbuję to jakoś zrozumieć
Dzięki
8 gru 17:37
Theosh: @ Trivial, możesz mi pomóc?
226738
8 gru 17:43
PW: Spojrzeć na zadnie następująco. Mamy
dwa białe pudełka. Pierwsze z nich to efekt
dorzucenia do dwóch monet pięciozłotowych i 3 monet dwuzłotowych jednej monety pięciozłotowej.
Drugie to efekt dorzucenia do dwóch monet pięciozłotowych i 3 monet dwuzłotowych jednej
monety dwuzłotowej. Zgodnie z treścią zadania należy przyjąć, że prawdopodobieństwo
natrafienia na pudełko B
1 jest równe
(takie jak prawdopodobieństwo wylosowania monety pięciozłotowej z zielonego pudełka), zaś
prawdopodobieństwo natrafienia na pudełko B
2 jest równe
(takie jak prawdopodobieństwo wylosowania monety pięciozłotowej z zielonego pudełka).
W pudełku B
1 jest 6 monet − trzy pięciozłotowe i trzy dwuzłotowe.
W pudełku B
2 jest 6 monet − dwie pięciozłotowe i cztery dwuzłotowe.
Doświadczenie polega na wylosowaniu dwóch monet z jednego z pudełek B
1 lub B
2.
Zdarzenie A − "wylosowano monety o sumie 7" ma więc następujące prawdopodobieństwa warunkowe
zaszyfrowane w treści zadania:
Zastosowanie wzoru na prawdopodobieństwo całkowite
P(A) = P(A|B
1)P(B
1) + P(A|B
2)P(B
2)
kończy rozwiazanie.
8 gru 17:49
8 gru 17:51
bezendu:
ciekawe czy na maturze Twoje rozwiązanie było by ok ?
8 gru 17:52
8 gru 18:01
bezendu:
8 gru 18:02
Mila:
Przepraszam podałam adres do innego zadania.
8 gru 18:08
bezendu:
Więc można prosić o to drzewko ?
8 gru 18:09
Trivial:
Drzewo jest następujące:
* {
5 {
2+2
2+5
5+5
}
2 {
2+2
2+5
5+5
}
}
8 gru 18:11
Mila:
Bezendu, co z tym drzewkiem, już wiesz, czy narysować?
9 gru 16:20
matyk: Wyjdź na dwór i wybierz dowolne drzewo i przerysuj
9 gru 16:26
bezendu:
Rozumiem zapis PW, ale drzewka nie potrafię rysować do doświadczeń wieloetapowych, przy
jednoetapowych nie mam z tym problemu. Więc proszę o rysunek.
9 gru 16:26
Mila:
Z: zielone pudełko
10x5 zł, 5x2zł
B: białe pudełko na początku
2x5zł; 3x2zł
Po wylosowaniu 5zł; B: 3x5zł, 3x 2zł 6 monet
Po wylosowaniu 2zł; B: 2x5zł, 4x 2zł 6 monet
9 gru 17:07
Mila:
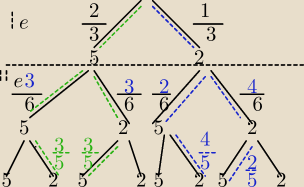
Lewa strona:
3x5zł, 3x 2zł 6 monet
Prawa strona
2x5zł, 4x 2zł 6 monet
A wylosowano z białego pudełka 7zł
| | 2 | | 3 | | 3 | | 2 | | 3 | | 3 | |
P(A)= |
| * |
| * |
| + |
| * |
| * |
| + |
| | 3 | | 6 | | 5 | | 3 | | 6 | | 5 | |
| | 1 | | 2 | | 4 | | 1 | | 4 | | 2 | |
+ |
| * |
| * |
| ++ |
| * |
| * |
| = |
| | 3 | | 6 | | 5 | | 3 | | 6 | | 5 | |
W tym zadaniu nie polecam drzewka , za duzo gałązek
9 gru 17:25
bezendu:
To jaki inny sposób na to zadanie ? Wiem, że jest to prawdopodobieństwo warunkowe ?
9 gru 17:26
Mila:
Masz sposób rozpisany u PW, prawdopodobieństwo całkowite.
9 gru 17:38
bezendu:
Dziękuję
Mila za rysunek, bo wiem, że nia łatwo tutaj rysować drzewka
9 gru 17:58
Mila:
To nie problem z rysowaniem, ale coś mi fiksuje przeglądarka, kilka razy wszystko mi znikało.
9 gru 18:04
bezendu:
Mila mam jeszcze pytanie odnośnie matury. Mam robić arkusze czy lepiej skupić się na
analitycznej, bryłach i prawdopodobieństwie ? Bo to akurat mi nie poszło na maturze roz.
9 gru 18:16
bezendu: ?
9 gru 18:59
Mila:
Na zmianę , przy trudnościach z arkuszem, szukaj innych zadań danego typu.
Co robicie na lekcjach?
9 gru 19:00
bezendu:
Teraz kończymy statystykę. W czwartek mam sprawdzian z prawdopodobieństwa. Ale jeszcze mam
pytanie odnośnie funkcji.
9 gru 19:02
bezendu:
mam taki wykres f(x)=|x2−2|x|| jak się za to zabrać, przedziały ?
9 gru 19:06
Piotr 10: Raz na iksa wartość bezwgledna a potem na całość a podstawowy wykres to y=x2−2x
9 gru 19:08
