wielomiany Bartek: Czy jest możliwe, żeby wielomian: W(x) = x³ − 2x² + 5 nie miał żadnych pierwiastków? Bo sprawdziłem wszystko: 1,−1, 5 i −5.

lolek betonek: https://matematykaszkolna.pl/strona/121.html

ZKS: Wielomian stopnia trzeciego zawsze posiada co najmniej jeden pierwiastek rzeczywisty.

Piotr 10: Sprawdziłeś tylko, czy ma wymierne pierwiastki. Nie ma ich. Ale nie sprawdziłeś możliwości, że ten wielomian może mieć niewymierne pierwiastki rzeczywiste

ICSP: Wielomian nieparzystego stopnia posiada zawsze nieparzystą liczbę pierwiastków ( licząc krotności)

ICSP: w(−2) * w(−1) < 0 ⇒ na przedziale (−2 ; −1) funkcja ma pierwiastek

Bartek: Tyle to ja też wiem. Sęk jednak w tym, że gdy podstawiam owe liczby do wielomianu, to ani razu nie wychodzi zero i tu jest szkopuł.

ICSP: No to żadna z liczb 1 , −1 , 5 , −5 nie jest pierwiastkiem wielomianu.

Bartek: A jak mogę sprawdzić istnienie pierwiastków niewymiernych rzeczywistych?

Bartek: ...oraz jak do nich dotrzeć?

ICSP: Wzory Cardano

Bartek: Okej, dzięki, ale to chyba bardziej w wikipedi trzeba poczytać,bo w tym serwisie prostszego objaśnienia chyba nie ma.

ICSP: https://matematykaszkolna.pl/forum/99243.html

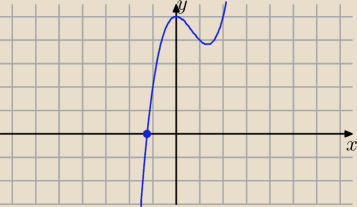
Bogdan: Można skorzystać tu z możliwości rysowania wykresów i zobaczyć, czy wykres funkcji ma punkty wspólne z osią x. Wykres y = x³ − 2x² + 5 ma jeden taki punkt, a więc funkcja f(x) = x² − 2x ² + 5 ma jeden pierwiastek.

Bartek: Hehe ICSP, ale widzę, że ty też tego kiedyś nie kumałeś. Ja też dzisiaj już jestem zbyt na takie rzeczy zmęczony. Może przysiądę jutro, a tym czasem ide dalej z łatwiejszym materiałem