proszę o odpowiedż ala: wyznacz wartości parametru m dla których równanie x − |4−2x|= 2m ma dwa rozwiązania a) dodatnie b) przeciwnych znaków ja to tak rozwiązała x−|2x − 4|=2m x−2|2−x| = 2m /: 2 x/2 − |x−2| = m f(x)= x/2 +x−2= 3/2x − 2 dla x należącego ( − nieskończoności , 2) czyli x< 2 f(x) = x/2 −x +2= − x/2 +2 dla x naleącego (2, + nieskończoności) czyli x>2 potem narysowałam wykres f(x) wyciągnęłam wniosek że a) m należy do (−2, 1) ma dwa rozwiązanie dodatnie b) dla m należącego do ( − nieskończoności , −2) ma rozwiązanie przeciwnych znaków czy takie rozwiązanie jest prawidłowe

Tadeusz: ... to może zacznij od sprawdzenia czy poprawnie zapisałaś treść zadania −

PW: |x−2| = x−2 dla x≥2 − zgubiłaś zero z dziedziny. f(2)=1 − dla m>1 rozwiązań nie ma (bo 1 jest maksimum funkcji f) Dla m=1 jest jedno rozwiązanie (ale o to nie pytali) Dla m∊(−2,1) są dwa rozwiązania dodatnie dla m=0 są dwa rozwiązania (ale jedno z mich jest zerem − o to nie pytali) dla m<0 rozwiązania są różnych znaków. Poza tym co napisałem w pierwszym zdaniu − wszystko w porządku. Dzielenie przez 2 chyba utrudnia narysowanie funkcji (ułamki). Lepiej było zostawić jak jest i rozstrzygnąć jakie musi być 2m, a dopiero w odpowiedzi podzielić przez 2.

Bogdan: Powtórzę jeszcze raz wczorajszą moją wypowiedź dotyczącą tego zadania i podam rozwiązanie. Osoby ala i piotr względnie ta sama osoba używająca tych dwóch nicków nie starają się niestety podjąć próby samodzielnego przeanalizowania zadania i ustalenia samemu wyników. 211232 oraz 211262 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Mamy równanie: x − |4 − 2x| = 2m Porządkujemy zapis: x − |2x − 4| = 2m. 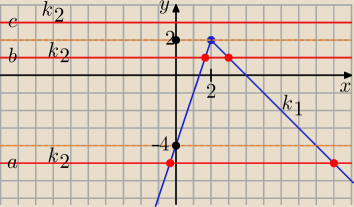Zapisujemy oddzielnie lewą stronę i prawą stronę w postaci wzorów pewnych linii: − linia k₁ (niebieski wykres): y = x − |2x − 4| y = x − |2x − 4| dla x < 2 przyjmuje wzór: y = x + 2x − 4 ⇒ y = 3x − 4 y = x − |2x − 4| dla x ≥ 2 przyjmuje wzór: y = x − 2x + 4 ⇒ y = −x + 4 − linia k₂ (czerwony wykres): y = 2m, to jest wykres funkcji stałej i to jest linia prosta równoległa do osi odciętych mogąca przyjmować w zależności od wartości parametru m dowolne położenie (narysowałem trzy przykładowe położenia tej linii: a, b, c) Rozwiązania równania x − |4 − 2x| = 2m są reprezentowane na rysunku przez punkty przecięcia tych dwóch linii. Widzimy, że są: a) dwa rozwiązania dodatnie wtedy, gdy dwa punkty przecięcia znajdą się po dodatniej (czyli prawej) stronie osi x, prosta y = 2m zawarta jest wtedy między prostymi y = −4 i y = 2, (położenie b) a więc trzeba rozwiązać nierówność: −4 < 2m < 2 ⇒ −2 < m <1 b) dwa rozwiązania przeciwnych znaków wtedy, gdy jeden punkt przecięcia linii jest po ujemnej stronie osi x, a drugi po stronie dodatniej, prosta y = 2m przyjmuje położenie poniżej prostej y = −4 (położenie a), otrzymujemy w tej sytuacji nierówność: 2m < −4 ⇒ m < −2 Odp.: Równanie x − |4 − 2x| = 2m ma dwa rozwiązania dodatnie dla m∊(−2, 1) oraz dwa rozwiązania przeciwnych znaków dla m∊(−∞, −2). Przepraszam, że tym razem (ale to naprawdę zrobiłem w drodze wyjątku) daję gotowca.

ala: dziękuję bardzo ale czy powyzsze rozwiązanie jest złe