Logarytmy
Piotr 10: Hej. Zacząłem robić logarytmy i mam taki problem z pewnymi przykładami:
a) 3 12 log316
b) 102+log3
Nie wiem jak zabrać się za te przykłady
21 sie 15:19
wredulus_pospolitus:
kluczowe jest skorzystanie z:
aloga x = x
21 sie 15:23
Piotr 10: | | 1 | |
a) jakby nie było ułamka |
| to by wynik wyszedł 16. Tylko, że nie wiem co dalej |
| | 2 | |
| | 1 | |
Pomnożyłem |
| *16=8 a w odpowiedzi wynik to 4 |
| | 2 | |
21 sie 15:28
21 sie 15:37
Piotr 10: log16 30,5 nie wiem co dalej
21 sie 15:41
Piotrek: a) 30,5log316=3log34=4
21 sie 15:44
Piotrek: drugi przyklad skorzystaj z log(xy)=logx + logy
21 sie 15:46
Piotr 10: Możesz mi wytlumaczyc jak zrobiles podpunkt a) ?
21 sie 15:47
aba:
312log316= 3log3 √16= .......... = 4
21 sie 15:47
aba:
102+log3= 102*10log3= 100*3 =..
21 sie 15:48
Piotrek: 30,5log316=3log34 skorzystalem z twierdzenia n*logba=logabn
potem
3log34=3log34=4 skorzystalem tu z alogax=x
21 sie 15:50
Piotr 10: aba a w tym poście 15:37 n*log
b a=log
b a
n nie powinno być? Z góry dziękuję wam za pomoc

Muszę wyjść z komputera
21 sie 15:50
aba:
Echhh źle wpisałam oznaczenia we wzorze ( przepraszam)
n*log
ba= log
ba
n 
21 sie 15:51
Piotrek: ajj ja rowniez nie sprawdziłem

ten sam błąd
21 sie 15:51
Piotr 10: A ok już wszystko jasne. Dziękuję jeszcze raz

Już wiem o co chodzi w dalszych przykładach

Będę pisał na pewno później problemy z moimi logarytmami

. Pozdrawiam
21 sie 15:52
aba:
i jeszcze taki ( bardzo przydatny):
21 sie 15:54
Piotrek: am to jest podstawa logarytmu a bn to liczba logarytmowana? czy dobrze to widze?
21 sie 15:59
aba: tak

21 sie 17:03
5-latek: Ten ostatni wzor co podala
aba −pozdrawiam

mozesz zastosowac m.innymi wtedy gdy
masz np w podstawie
√5 bo zapiszsesz to wtedy 5
1/2 i wtedy 2 wylaczasz przed logarytm
lub masz np w podstawie U{1}4} bo mozesz zapisac wtedy 4
−1 i wtedy (−1) dajasz przed
logarytm
22 sie 20:56
kos:
zad 1 Wykaż,że dla m= 5log37−7log35
liczba 2013m+5 jest liczbą pierwszą
22 sie 21:42
Piotr 10: Porównaj liczby a i b, jeśli:
a) a=log
2√2 i b=log
2√3
2
a=
√2 i 2
b=
√3
b>a, gdyż
√3>
√2
b)a=log
138 i b=log
139
(3
−1)
a=8 b=−2
a>b
c)a=log
27 i b=log
37
2
a=7 i 3
b=7
a>b
| | 1 | | 1 | |
d)a=log23 |
| i b=log13 |
| |
| | 5 | | 5 | |
| | 2 | | 1 | | 1 | | 1 | |
( |
| )a= |
| i ( |
| )b= |
| |
| | 3 | | 5 | | 3 | | 5 | |
a>b
Można w ten sposób zrobić te zadanie?
22 sie 21:48
kos:
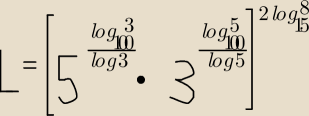 zad 2
zad 2 Zapisz liczbę
L w postaci potęgi liczby
2
22 sie 21:50
ZKS:
Tu chyba nie potrzeba pomocy?

To zadanie jest dla kogoś?

22 sie 21:50
Piotr 10: ZKS możesz spojrzeć na post 22 sie 21:48 ?

22 sie 21:51
kos:
To są
zadania dla
właściciela postu

22 sie 21:52
Piotr 10: kos ja na razie nie ruszę takich zadań, które podałeś, bo dopiero zaczynam logarytmy
22 sie 21:53
Piotr 10: Ale na pewno je spróbuję zrobić jak już opanuje lepiej logarytmy

22 sie 21:53
6-latek:
Zadanie 2 chyba z Pazdro

22 sie 21:54
kos:
ok

( ale one nie są trudne, nawet jak dla Ciebie

22 sie 21:54
ZKS:
Czy to tak wygląda?
(5log100 3/log 3 * 3log100 5/log 5)2log158
22 sie 21:55
kos:
zad2/ nieco zmodyfikowane

22 sie 21:55
kos:
No przecież.....
pięknie wyrysowałem

22 sie 21:56
Piotr 10: Tak z Pazdro są te zadania. Pazdro naprawdę dobry zbiór. Możecie sprawdzić moje rozwiązanie
post 22 sie 21:48 ? prośba

. Bo nie wiem czy to jakoś uzasadniać czy nie
22 sie 21:57
ZKS:
Piotr 10 można tak robić.

22 sie 21:57
ZKS:
Wyrysowałem czy wyrysowa
łam?

22 sie 21:57
Piotr 10: A można jakoś inaczej? Bo moja p.profesor na pewno będzie chciała uzasadnienie szczegółowe
22 sie 21:58
kos:
W zad 1/ powinno być 2013m+ 4
22 sie 21:58
kos: 
22 sie 21:58
Piotr 10: Eta 100%

22 sie 21:59
ZKS:
Można też tak. Zakładamy że jedna z liczb jest większa
log
2√2 < log
2√3 opuszczamy logarytmy i mamy
√2 <
√3 zatem prawda. Dostajemy że log
2√2 jest mniejsze od log
2√3.

22 sie 22:00
Piotr 10: a ten przykład d)?Można lepiej uzasadnić?
22 sie 22:03
kos:
1/ a= log2 √2 i b= log2 √3
funkcja logarytmiczna y=log2x , x>0 jest rosnąca
zatem dla większych argumentów osiąga większe wartości
to: ....... dokończ
22 sie 22:04
kos:
Ejjj ...
ZKS 
nie można pisać
"opuszczamy logarytmy"
22 sie 22:06
ZKS:
Znowu zakładamy że jedna z liczb jest większa
| | 2 | | 1 | |
log1/5 |
| < log1/5 |
| [zmieniamy zwrot nierówności (dlaczego?)] |
| | 3 | | 3 | |
| | 1 | | 1 | |
Otrzymaliśmy że log2/3 |
| jest większe od log1/3 |
| . |
| | 5 | | 5 | |
22 sie 22:09
Garth:
Jak wiec powinnismy pisac?
22 sie 22:09
ZKS:
Wiem przepraszam za te słownictwo ale tak już sobie wmówiłem.

22 sie 22:10
Piotr 10: Czyli b>a ok

. Jeszcze do funkcji logarytmicznej nie doszedłem i dlatego na to nie wpadłem.
Zaraz spróbuje tym sposobem zrobić te 3 przykłady dalsze

22 sie 22:10
ZKS:
Ze względu na różnowartościowość funkcji logarytmicznej nierówność ta jest równoważna
nierówności.

22 sie 22:12
kos:
Z różnowartościowości funkcji logarytmicznej
log2c = log2d ⇒c=d . c>0 id>0
22 sie 22:12
kos:
No ... teraz ok

22 sie 22:13
Piotr 10: b)a=log138 i b=log139
Jest to funkcja logarytmiczna malejąca, gdyż a∊(0;1)
Wraz ze wzrostem argumentów wartości funkcji maleją, a więc
a>b dobrze?
22 sie 22:15
kos:
Baaaaaaaaaaaaaaaaaaaaardzo dobrze

22 sie 22:16
Piotr 10: A co z przykładami c) d) ? Tam są już inne podstawy. Ma to chyba wpływ jakiś
22 sie 22:17
kos:
Masz kolizję oznaczeń
zapisz tak : dla podstawy logarytmu 13€(0,1)
22 sie 22:19
Piotr 10: faktycznie mój błąd. Eh na stronce było ze a∊(0;1) i dlatego

22 sie 22:21
kos:
c) i d) zauważ ,że masz jednakowe liczby logarytmowane
zatem co z własnością funkcji logarytmicznej......... 100% wiesz

22 sie 22:21
22 sie 22:24
Piotr 10: Właśnie nie za bardzo, sam się uczę logarytmów a funkcje logarytmiczną jutro zaczynam a te
zadanie było przed tą funkcją
22 sie 22:24
Piotr 10: c)a=log27 i b=log37
a>b
Tak wywnioskowałem z przykładowych wykresów funkcji logarytmicznej
Jeżeli liczby logarytmowane są takie same, a wartości podstaw są różne, to im większa podstawa
tym mniejsza wartość funkcji, tak?
22 sie 22:30
Piotr 10: Jeszcze trzeba dodać, że musi być to funkcja rosnąca
22 sie 22:33
kos:
I oto chodziło

22 sie 22:34
kos:
A dla ........ log1/2 7 i log1/37 ?
22 sie 22:35
Piotr 10: a w d) Są to obydwie funkcje malejące, a więc będzie na odwrót im większa podstawa tym większe
wartości funkcji, tak?
22 sie 22:35
Piotr 10: log
1/27 jest większe uzasadnienie post wyżej

22 sie 22:36
kos:
No i teraz ... "wchodź na głębszą wodę" z logarytmami........

zapoznaj się z podstawowymi wzorami
22 sie 22:38
22 sie 22:39
Piotr 10: Już zapoznałem się, porobiłem zadania z Pazdro 1 temat zrobiony cały. Trudny był taki przykład:
log
320=a i log
315=b i trzeba było policzyć log
2360, ale już wiem jak go zrobić. Jutro
przechodzę do wyznaczania dziedziny(ale to proste jest zwykła funkcja wymierna) i rysowanie
wykresów funkcji

22 sie 22:41
Piotr 10: Z tej strony co mi podałaś to tylko ''uzasadnienie'' tych wzorów porobię, ale większości to
wiem czemu takie są

22 sie 22:43
kos:
Ok

To powoli do

22 sie 22:47
Garth: Piotr 10, jestes obecnie uczniem szkoly sredniej?
22 sie 22:50
Piotr 10: Tak, idę we wrześniu do 3 klasy liceum

.
kos ja to jeszcze mecz oglądam

22 sie 22:52
Piotr 10: A czemu pytasz?
22 sie 22:53
Garth: Z ciekawosci.

Dobrze, ze sie uczysz rowniez w wakacje.

22 sie 23:02
tim: W poszukiwaniach Ety...
22 sie 23:03
Piotr 10: 

22 sie 23:05
Eta:
Hej
tim 
...........

z radości
No wreszcie się zjawiłeś

Co u Ciebie ? O ile mnie pamięć nie myli, to będziesz świeżo upieczonym studentem? tak?
Jaki kierunek studiów wybrałeś? ( jeżeli można wiedzieć)
Pozdrawiam

22 sie 23:11
ZKS:
Pierwsi osadnicy na tej stronie.

22 sie 23:12
Eta:
ZKS tak, dokładnie

22 sie 23:15
Eta:
Tylko atmosfery tamtych czasów ..... szukać i szukać (ale już jej nie ma)

22 sie 23:16
tim: Tak, osadnicy.
5 lat temu.
Jak zobaczyłem, ze wciąż jesteś, strasznie się ucieszyłem.
Obiecywałem sobie tu powrót, ale matura i liceum zrobiła swoje.
Tak, teraz studia.
Chciałbym porozmawiać z Tobą (dziś już za późno), ale prywatnie. Mam nadzieję, że będziesz
miała czas. Ogród wspaniały?

22 sie 23:19
Eta:
Bardzo się cieszę

i witam w "ogrodzie" ... w godzinach popołudniowych (ok 18
oo
Rozpalić grila ?

22 sie 23:28
tim: Jeżeli w miejscowości K−J to październik otworem.

Jutro złapię. Tymczasem pora spać. Dobranoc.
22 sie 23:31
Eta: Miłych snów

22 sie 23:33
ZKS:
Dobra ja dam jeszcze coś dla
Piotra 10 na później i nie przeszkadzam.

Rozwiązać nierówność
log
1253 * log
x5 + log
98 * log4(x) > 1.
22 sie 23:38
Garth: log4(x); tutaj 4 czy 10 to podstawa?
22 sie 23:53
Godzio:
Na pewno 4

22 sie 23:55
ZKS:
Oczywiście jak pisze
Godzio.

Mam takie pytanko do Ciebie kupujesz BF 4?

22 sie 23:58
Godzio: Ciężko powiedzieć

Nie wiem czy mi pójdzie, a na razie mam praktycznie 0 czasu na CoH−a 2, w
którego mógłbym grać ciągle

23 sie 00:02
 Muszę wyjść z komputera
Muszę wyjść z komputera

 ten sam błąd
ten sam błąd
 Już wiem o co chodzi w dalszych przykładach
Już wiem o co chodzi w dalszych przykładach  Będę pisał na pewno później problemy z moimi logarytmami
Będę pisał na pewno później problemy z moimi logarytmami  . Pozdrawiam
. Pozdrawiam

 mozesz zastosowac m.innymi wtedy gdy
masz np w podstawie √5 bo zapiszsesz to wtedy 51/2 i wtedy 2 wylaczasz przed logarytm
lub masz np w podstawie U{1}4} bo mozesz zapisac wtedy 4−1 i wtedy (−1) dajasz przed
logarytm
mozesz zastosowac m.innymi wtedy gdy
masz np w podstawie √5 bo zapiszsesz to wtedy 51/2 i wtedy 2 wylaczasz przed logarytm
lub masz np w podstawie U{1}4} bo mozesz zapisac wtedy 4−1 i wtedy (−1) dajasz przed
logarytm
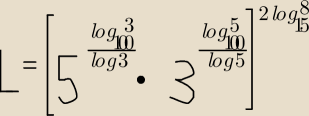 zad 2 Zapisz liczbę L w postaci potęgi liczby 2
zad 2 Zapisz liczbę L w postaci potęgi liczby 2
 To zadanie jest dla kogoś?
To zadanie jest dla kogoś? 




 ( ale one nie są trudne, nawet jak dla Ciebie
( ale one nie są trudne, nawet jak dla Ciebie 


 . Bo nie wiem czy to jakoś uzasadniać czy nie
. Bo nie wiem czy to jakoś uzasadniać czy nie





 nie można pisać "opuszczamy logarytmy"
nie można pisać "opuszczamy logarytmy"

 . Jeszcze do funkcji logarytmicznej nie doszedłem i dlatego na to nie wpadłem.
Zaraz spróbuje tym sposobem zrobić te 3 przykłady dalsze
. Jeszcze do funkcji logarytmicznej nie doszedłem i dlatego na to nie wpadłem.
Zaraz spróbuje tym sposobem zrobić te 3 przykłady dalsze 







 zapoznaj się z podstawowymi wzorami
zapoznaj się z podstawowymi wzorami



 To powoli do
To powoli do 
 . kos ja to jeszcze mecz oglądam
. kos ja to jeszcze mecz oglądam 
 Dobrze, ze sie uczysz rowniez w wakacje.
Dobrze, ze sie uczysz rowniez w wakacje. 


 ...........
...........  z radości
No wreszcie się zjawiłeś
z radości
No wreszcie się zjawiłeś Co u Ciebie ? O ile mnie pamięć nie myli, to będziesz świeżo upieczonym studentem? tak?
Jaki kierunek studiów wybrałeś? ( jeżeli można wiedzieć)
Pozdrawiam
Co u Ciebie ? O ile mnie pamięć nie myli, to będziesz świeżo upieczonym studentem? tak?
Jaki kierunek studiów wybrałeś? ( jeżeli można wiedzieć)
Pozdrawiam 




 i witam w "ogrodzie" ... w godzinach popołudniowych (ok 18oo
Rozpalić grila ?
i witam w "ogrodzie" ... w godzinach popołudniowych (ok 18oo
Rozpalić grila ? 
 Jutro złapię. Tymczasem pora spać. Dobranoc.
Jutro złapię. Tymczasem pora spać. Dobranoc.

 Rozwiązać nierówność
log1253 * logx5 + log98 * log4(x) > 1.
Rozwiązać nierówność
log1253 * logx5 + log98 * log4(x) > 1.

 Mam takie pytanko do Ciebie kupujesz BF 4?
Mam takie pytanko do Ciebie kupujesz BF 4? 
 Nie wiem czy mi pójdzie, a na razie mam praktycznie 0 czasu na CoH−a 2, w
którego mógłbym grać ciągle
Nie wiem czy mi pójdzie, a na razie mam praktycznie 0 czasu na CoH−a 2, w
którego mógłbym grać ciągle 