pole obszaru postać parametryczna
kendzior:
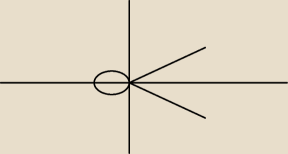
Witam wszystkich mam problem z rozwiązaniem zadania mam podaną funkcję w postaci parametrycznej
:
x=t
2−1
y=t
3−t
i mam policzyć pole obszaru nie mając granicy, i tutaj mam problem :
t
3−t=0
t(t
2−1)=0
t=0 t=−1 t=1
co będzie granicą całkowania bo jak dla mnie to t=−1/1 bo wtedy przecina oś ox chyba, że źle
narysowałem wykres.
jest wzór ∫ od a −b | y(t)* pochodna x(t)|
pochodna x(t)= 2t
po podstawieniu pod wzór wychodzi całka
∫t
4−t
2 dt no i dalej normalnie
jedyny problem polega na granicach całkowania, zadania zrobiłem (wydaje mi się poprawnie)
jednak w odpowiedziach jest 1/2ln3

pozdrawiam i liczę na pomoc, już nakląłem tyle, że na bank pójdę do piekła pozdrawiam
6 sie 18:14
AS: Mój wstępny wynik to: 8/15
Jak znajdę trochę czasu to jutro pomyślę.
6 sie 19:26
Mila:
Jest policzona na forum, szukaj .
6 sie 19:32
6 sie 19:39
kendzior: witam ponownie, dałem radę rozwiązać to zadanie tylko mam parę pytań a Wasza odpowiedź pomoże
mi zrozumieć zagadnienia.
1. Czy moje granice całkowania są poprawnie wyznaczone ? To znaczy czy dobrze rozumiem ich
istnienie, czyli granice całkowania to miejsce w których wykres przecina os ox czyli jest to
punkt 0 dla wartości t = −1 i 1 czyli granice całkowania to −1/1.
Bo w przykładzie który podała @Mila ( wielkie dzięki za to), całka jest rozbita na 2 oznaczone
od −1/0 i 0/1 więc wyjdzie na to samo.
2. Nie rozumiem dlaczego w tamtym przykładzie:
P = −−1∫0(t3−t)*2t dt +→→ 0∫1 (t−t3)2t ←←dt =
−1∫0(t−t3)*2t dt + 0∫1 (t−t3)*2t dt = została zamieniona kolejność, czy to nie da tego samego ?
Przecież to jest ta sama całka tylko ma granice całkowania inne.
Przykład zrobiłem jeszcze raz i wyszedł mi dobrze niby −8/15 ale we wzorze jest moduł.
Mam również problem z przykładem dotyczącym pola powierzchni bryły:
x=cos3t
y=sin3t
obliczam pochodne podstawiam pod wzór dochodzę do momentu gdzie mam do policzenia całkę
∫sin4xcos2dx , i nie wiem co z nią zrobić.
Zamieniam sin4x na (sin2x)2cos2xdx
następnie za sin2x wstawiam 1/2(1−cos2x)
więc mam do policzenia całki
∫cos2x
∫2cos22x
∫cos42x
i tutaj problem czy mam podstawić za t=2x i liczyć całki cos 2 i cos4, czy jest jakiś inny
sposób którego nie zauważam.
Dziękuję za wszystkie odpowiedzi i liczę, że i tym razem mnie nie zawiedziecie. Pozdrawiam
6 sie 21:29
Mila:
1) Pętla jest symetryczna względem OX i dlatego sa 2 całki w granicach od −1 do 0.(wzór górnego
wykresu)
W postaci parametrycznej jutro wytłumaczę, dziś już nie myślę, późno i gorąco.
2) całkę policzę
Taka:
∫sin4xcos2x dx
6 sie 22:52
Mila:
Może jest łatwiejszy sposob, ale mam taki (dużo pisania)
∫sin
4x*(1−sin
2x)dx=∫sin
4x dx−∫sin
6x dx
J
1=∫sin
4x dx=∫sin
3x *sinx dx=
[sin
3x=u, 3sin
2x cosx dx =du; dv=sinx dx, v=−cosx]
cd.=−sin
3xcosx+3∫sin
2x cos
2x dx=−sin
3x cosx+3∫sin
2x*(1−sin
2x) dx⇔
∫sin
4xdx=−sin
3x cosx+3∫sin
2xdx−3∫sin
4x dx⇔(przenoszę ostatnią całkę na lewą stronę)
| | 3 | |
4∫sin4xdx=−sin3x cosx+ |
| ∫(1−cos2xdx) |
| | 2 | |
| | 3 | | 3 | | 1 | |
4∫sin4xdx=−sin3x cosx+ |
| x− |
| * |
| sin2x⇔ |
| | 2 | | 2 | | 2 | |
| | 1 | | 3 | | 3 | |
∫sin4x dx= − |
| sin3x cosx+ |
| x− |
| sin2x |
| | 4 | | 8 | | 16 | |
Drugą całkę policz podobnie.
W razie kłopotów jutro napiszę.
6 sie 23:31
kendzior: No właśnie taki sposób, też brałem pod uwagę, wielkie dzięki za rozwiązania − dalej dałem radę
sam.
Mogłabyś mi jeszcze wytłumaczyć postać parametryczną ? Dowiedziałem się, że nie jest to
wymagane na mojej uczelni ale już za daleko zabrnąłem.
Pozdrawiam i jeszcze raz dziękuję.
7 sie 12:58
7 sie 16:40
7 sie 16:49
AS: Z postaci parametrycznej przechodzę do postaci y = f(x)
x = t
2 − 1 ⇒ t
2 = x + 1
y = t
3 − t = t*(t
2 − 1) =
√x + 1*(x
2 + 1 − 1)
y = x*
√x + 1
Granice całkowania od −1 do 0
| | 2*(3*x − 2) | |
J = ∫x*√x + 1 = |
| *√(x + 1)3 |
| | 15 | |
Po podstawieniu granic całkowania otrzymujemy
P = |−4/15| = 4/15
Jest to pole połowy szukanego obszaru
7 sie 17:59
AS: Korekta − w drugim wierszu ma być ... √x + 1*(x + 1 − 1)
7 sie 18:23
kendzior: Bondziorno !
Ruszyłem dalej z materiałem i mam pytanie mam do policzenia całkę podwójną po obszarze
x
2+y
2<2 x
2+y
2
∫dr 0/2 ∫0/2π [(rcosϱ)
2+(rsinϱ)
2]rdϱ
dalej robię tak, że wyciągam r
3 a cos
2 + sin
2 to 1, więc mam do policzenia całkę ∫r
3dϱ,
wyciągam r
3 zostaje mi dϱ, wynik to r
3ϱ.
W granicach 0/2π wychodzi 2πr
3
dalej liczę z tego całke 2π∫r
3dr → (r
4π)/2
granice całkowania 0/2
więc 16π/2 = 8π
jednak wynik to 2π, gdzie robię błąd ?
pozdrawiam, i nie dajcie się upałom

9 sie 23:19
kendzior:
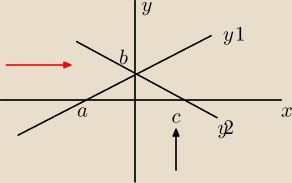
to ja od razu z drugim problemem

, mam przykład całką z trójkąta
A (−4,0), B(0,2) C (2,0), są to inaczej 3 proste x=0, y1=1/2x+2, y2=−x+2, można to policzyć
jako sumę dwóch obszarów, różnie ograniczonych, najpierw całka
∫−4,0 dx ∫ 0, 1/2x+2 (1+x−y)dy + ∫0,2 dx ∫ 0, −x+2 (1+x−y)dy − wtedy wychodzi −2, jednak można
zamienić to na całkę w innej kolejności, nie wiem jak to się poprawnie nazywa

,
wtedy to będzie
∫0,2 dy ∫ 2y−4, 2−y (1+x−y)dx wtedy też wychodzi −2 ... w odpowiedziach jest 2, jednak gdy
zamieni się granice całkowania na odwrót, wtedy wychodzi 2, ale chyba wtedy są źle, bo
ograniczona jest y2 z góry i y1 z dołu, chyba, że się mylę

Ale jeśli liczę najpierw po y potem po x to patrzę na wykres od strony czarnej strzałki, a gdy
po x potem po y (zamiana) wtedy od strony czerwonej strzałki, mam rację ?

10 sie 01:18
Mila:
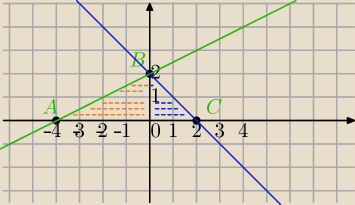
A (−4,0), B(0,2), C (2,0)
AB: y=ax+b
y=ax+2
−4a+2=0
BC:
y=ax+2
2a+2=0
a=−1
y=−x+2
1
0 Całkowanie względem zmiennej y, a następnie względem x (w stałych granicach)
−4∫
0 [
0∫
0,5x+2(1+x−y)dy]dx=−4
0∫
2 [
0∫
−x+2(1+x−y)dy]dx=2
po dodaniu wynik :−2
2
0 Całkowanie względem zmiennej x, a następnie względem y (w stałych granicach)
Ustalamy granice
dolna granica x=2y−4
górna granica x=2−y
dolna granica y=0
górna granica y=2
0∫
2 [
2y−4∫
2−y(1+x−y) dx]dy=−2
10 sie 17:52
10 sie 18:46
Mila:
Trivial Dziękuję pięknie za sprawdzenie

10 sie 19:03
kendzior: Dzięki, mógłby ktoś jeszcze sprawdzić tą całkę co dałem przed zadaniem z trójkątem ? Pozdrawiam
11 sie 10:43
 Witam wszystkich mam problem z rozwiązaniem zadania mam podaną funkcję w postaci parametrycznej
:
x=t2−1
y=t3−t
i mam policzyć pole obszaru nie mając granicy, i tutaj mam problem :
t3−t=0
t(t2−1)=0
t=0 t=−1 t=1
co będzie granicą całkowania bo jak dla mnie to t=−1/1 bo wtedy przecina oś ox chyba, że źle
narysowałem wykres.
jest wzór ∫ od a −b | y(t)* pochodna x(t)|
pochodna x(t)= 2t
po podstawieniu pod wzór wychodzi całka
∫t4−t2 dt no i dalej normalnie
jedyny problem polega na granicach całkowania, zadania zrobiłem (wydaje mi się poprawnie)
jednak w odpowiedziach jest 1/2ln3
Witam wszystkich mam problem z rozwiązaniem zadania mam podaną funkcję w postaci parametrycznej
:
x=t2−1
y=t3−t
i mam policzyć pole obszaru nie mając granicy, i tutaj mam problem :
t3−t=0
t(t2−1)=0
t=0 t=−1 t=1
co będzie granicą całkowania bo jak dla mnie to t=−1/1 bo wtedy przecina oś ox chyba, że źle
narysowałem wykres.
jest wzór ∫ od a −b | y(t)* pochodna x(t)|
pochodna x(t)= 2t
po podstawieniu pod wzór wychodzi całka
∫t4−t2 dt no i dalej normalnie
jedyny problem polega na granicach całkowania, zadania zrobiłem (wydaje mi się poprawnie)
jednak w odpowiedziach jest 1/2ln3  pozdrawiam i liczę na pomoc, już nakląłem tyle, że na bank pójdę do piekła pozdrawiam
pozdrawiam i liczę na pomoc, już nakląłem tyle, że na bank pójdę do piekła pozdrawiam
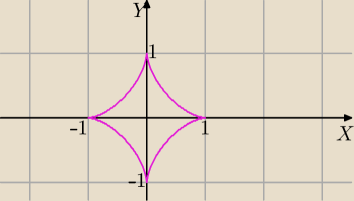 1) Tu jest opracowaniedo zadania 1
http://oen.dydaktyka.agh.edu.pl/dydaktyka/matematyka/c_analiza_dla_leniwych/zestaw4/zestaw4/zad4zestaw4.pdf
2) Asteroida
x(t)=cos3t
y(t)=sin3t
to jest równanie asteroidy i wg mnie obliczyłeś pole ograniczone asteroidą.(tak chciałeś, bo
napisałeś , że ma byc pow. bryły obrotowej)
1) Tu jest opracowaniedo zadania 1
http://oen.dydaktyka.agh.edu.pl/dydaktyka/matematyka/c_analiza_dla_leniwych/zestaw4/zestaw4/zad4zestaw4.pdf
2) Asteroida
x(t)=cos3t
y(t)=sin3t
to jest równanie asteroidy i wg mnie obliczyłeś pole ograniczone asteroidą.(tak chciałeś, bo
napisałeś , że ma byc pow. bryły obrotowej)

 to ja od razu z drugim problemem
to ja od razu z drugim problemem  , mam przykład całką z trójkąta
A (−4,0), B(0,2) C (2,0), są to inaczej 3 proste x=0, y1=1/2x+2, y2=−x+2, można to policzyć
jako sumę dwóch obszarów, różnie ograniczonych, najpierw całka
∫−4,0 dx ∫ 0, 1/2x+2 (1+x−y)dy + ∫0,2 dx ∫ 0, −x+2 (1+x−y)dy − wtedy wychodzi −2, jednak można
zamienić to na całkę w innej kolejności, nie wiem jak to się poprawnie nazywa
, mam przykład całką z trójkąta
A (−4,0), B(0,2) C (2,0), są to inaczej 3 proste x=0, y1=1/2x+2, y2=−x+2, można to policzyć
jako sumę dwóch obszarów, różnie ograniczonych, najpierw całka
∫−4,0 dx ∫ 0, 1/2x+2 (1+x−y)dy + ∫0,2 dx ∫ 0, −x+2 (1+x−y)dy − wtedy wychodzi −2, jednak można
zamienić to na całkę w innej kolejności, nie wiem jak to się poprawnie nazywa  ,
wtedy to będzie
∫0,2 dy ∫ 2y−4, 2−y (1+x−y)dx wtedy też wychodzi −2 ... w odpowiedziach jest 2, jednak gdy
zamieni się granice całkowania na odwrót, wtedy wychodzi 2, ale chyba wtedy są źle, bo
ograniczona jest y2 z góry i y1 z dołu, chyba, że się mylę
,
wtedy to będzie
∫0,2 dy ∫ 2y−4, 2−y (1+x−y)dx wtedy też wychodzi −2 ... w odpowiedziach jest 2, jednak gdy
zamieni się granice całkowania na odwrót, wtedy wychodzi 2, ale chyba wtedy są źle, bo
ograniczona jest y2 z góry i y1 z dołu, chyba, że się mylę  Ale jeśli liczę najpierw po y potem po x to patrzę na wykres od strony czarnej strzałki, a gdy
po x potem po y (zamiana) wtedy od strony czerwonej strzałki, mam rację ?
Ale jeśli liczę najpierw po y potem po x to patrzę na wykres od strony czarnej strzałki, a gdy
po x potem po y (zamiana) wtedy od strony czerwonej strzałki, mam rację ? 
 A (−4,0), B(0,2), C (2,0)
AB: y=ax+b
y=ax+2
−4a+2=0
A (−4,0), B(0,2), C (2,0)
AB: y=ax+b
y=ax+2
−4a+2=0

