Oblicz pola figur ograniczonych krzywymi: nas: Mam problem z taką całką:

⎧	x(t)=x2−1
⎩	y(t)=t3−t

Próbowałem narysować wyrkes ale wychodzi mi dziwna figura. Niewiem czy dobrze określam miejsca zerowe ale wychodzi mi x=0, x=−1 z obliczeń wychodzi mi :

2		2
	t5−		t3
5		3

W odpowiedziach jest podany wynik:

1
	ln3
2

Proszę o pomoc

AS: czy x(t) = x² − 1? a może t² − 1

nas: Tak własnie. Przepraszam za pomyłkę

Basia: y(t) = t³−t = t(t²−1) = t(t−1)(t+1) y(t) = 0 ⇔ t= −1 lub t=0 lub t=1 w przedziale <−1;1> funkcje x(t) = t²−1 i y(t) = t³−t są ciągłe ale funkcja x(t) jest w przedziale <−1;0> malejąca a w przedziale <0;1> rosnąca zatem P = −₋₁∫⁰|y(t)*x'(t)dt+ ₀∫¹ |y(t)|*x'(t) dt = ₀∫¹ |t³−t|*2t dt t³−t = t(t²−1) = t(t−1)(t+1) ≥0 dla t∊<−1;0> t³−t = t(t²−1) = t(t−1)(t+1) ≤0 dla t∊<0;1> czyli mamy P = −₋₁∫⁰(t³−t)*2t dt + ₀∫¹ (t−t³)²t dt = ₋₁∫⁰(t−t³)*2t dt + ₀∫¹ (t−t³)*2t dt = ₋₁∫¹ (t−t³)*2t dt = 2*₋₁∫¹(t²−t⁴)dt = 2*[ ¹₃t³ − ¹₅t⁵]₋₁¹ = 2*[ (¹₃−¹₅) − (−¹₃+¹₅) ] =

	10−6		8
2*[ 23 − 25 ] = 2*		=
	15		15

albo coś źle przepisałeś, albo czytasz niewłaściwą odpowiedź, albo jest błąd w odpowiedziach

nas: Witam dziękuje za odpowiedź. Ogólnie to nie pierwszy raz jak w odpowiedziach znajduje się błędna odpowiedź.Sprawdzam czasem moje wyniki w programach typu "Derive" i tak właśnie wychodzi. Wykres ładnie mi narysowała strona http://www.wolframalpha.com/input/?i=x%3Dt^2-1%2C+y%3Dt^3-t i wynik mam taki sam jak TY. Pozdrawiam.

Trivial: Z rysunku granice są takie: x = −1 do x = 0 czyli t = 0 do t = −1 (górna część) P = 2*∫₋₁⁰ y(x)dx = 2*∫₀⁻¹ y(t)x'(t)dt = 2*∫₀⁻¹(2t⁴−2t²)dt =

	t5		t3		1		1		8
= 4*[		−		]0−1 = 4*(		−		) =		.
	5		3		3		5		15

Taki sam wynik po raz kolejny → na pewno błąd w odpowiedziach.

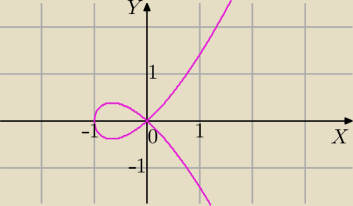
Mila: Wykres pętli. y=x√x+1 y=−x√x+1

	8
P=
	15

Basia: witajcie właśnie chciałam dopisać, że w tym przykładzie można też całkować po x P = 2*₋₁∫⁰ x√x+1 dx i wcale nie jest trudno tę całkę policzyć a dlaczego tak to już wynika z zapisu i rysunku Mili

Mila: Witaj Basiu, tak to ładnie rozpisałaś w postaci parametrycznej, że usunęłam swój wpis wczorajszy, był mniej dokładny.

Basia: Witaj Milu Cieszę się, że Ci się podoba, ale ta "śliczność" to głównie efekt lenistwa. Nie chciało mi się rysować więc rozpisałam "od a do z" algebraicznie