pole powierzchni (studia!) Marek: Oblicz pole powierzchni, która powstaje z obrotu dookoła osi OX krzywej o równaniu: http://img441.imageshack.us/img441/5109/dpw.png bardzo prosze o pomoc!

Magda: jakby ktoś mógł przynajmniej mnie nakierować ? niestety nie było mnie na wykładzie i nie wiem jak się za to zabrać

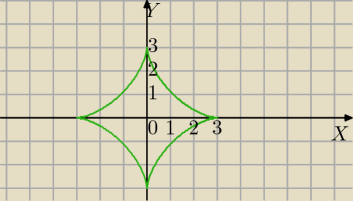
Mila: To jest wzór asteroidy, szukaj , są rozwiązania w postaci parametrycznej.

Mila: x^2₃+y^2₃=a^2₃ rownanie asteroidy. Wygodniej będzie skorzystać z postaci parametrycznej x(t)=acos³(t), a>0 y(t)=a sin³(t) [ na rysunku a=3] Korzystając z symetrii wykresu rozważymy tylko w I ćwiartce

	π
t∊<0,		>
	2

(1) S₁=2π₀∫^π₂|y(t)|*√(x'(t ))²+(y'(t))² dt x'(t)=−3acos²(t)sin(t) y'(t)=3asin²(t)cos(t) S₁=2π₀∫^π₂[(asin³(t)√9a²cos⁴(t)sin²(t)+9a²sin⁴(t)cos²(t)]dt= =2π₀∫^π₂[(3a²sin³(t)*√cos²(t)*sin²(t)*(cos²(t)+sin²(t))]dt= =6a²π₀∫^π₂[sin³(t)*√sin²(t)*cos²t]dt= =6πa²₀∫^π₂sin⁴(t)cos(t) dt = [ sint≥0 i cost≥0 dla

	π
t∊<0,		>]
	2

podstawienie[sint=u, cost dt=du]

	sin5		π   sin5   2		6πa2
= [6πa2		]0π2=6πa2		−6a2*0=
	5		5		5

	12πa2
P=2*S1=
	5

Sprawdź w notatkach, że spełnione są warunki, aby stosować wzór (1)