Prosze
Nie umiem matematyki:
Prosze o zadania , ktore rozwinal moje zdolnosci matematyczne

Moj zakres to:
1. Dialania w zbiorach liczbowych
2. Wyrażenia algebraiczne
3. Geometria płaska−pojecia wstępne
4. Geometria płaska −trójkąty
5.Trygonometria
6.Geometria płaska −pole koła , pole trójkąta
7. Funkcja i jej własności
8.Przeksztalcenia wykresów funkcji.
Dziękuje

24 lip 21:42
24 lip 21:45
bezendu:
Wyznacz wszystkie trójki liczb pierwszych a, b, c, dla których a2=b2+c
24 lip 21:45
Saizou : | | π | |
naszkicuj wykres funkcji g(x)=sin(2x+ |
| ), gdzie x∊R, a następnie ustal liczbę rozwiązań |
| | 3 | |
równania lg(x)l=0,8 należących do zbioru <0:2π>
24 lip 21:54
24 lip 21:56
24 lip 21:57
Mila:
1) Wyznacz długość odcinka dwusiecznej kąta prostego w trójkącie prostokątnym o
przyprostokątnych 6cm, 8cm.
2) w trójkącie prostokątnym jedna z przyprostokątnych jest dwa razy mniejsza od
przeciwprostokątnej. wyznacz stosunek pola koła opisanego na tym trójkącie do pola koła
wpisanego w ten trójkąt.
Zadania rozwiązywać ze starannymi zapisami.
Wykonać rysunki z oznaczeniami. Jeśli czegoś nie umiesz, to pytaj.
Treści zadań dostosowane do programu.
24 lip 21:59
Mateusz:
| | 1998*1999+2 | |
1) Czy |
| jest liczbą naturalną? |
| | (1998)2+2000 | |
2) (
√2−1)
6 zapisz w postaci: (a−b
√2)
3
3) Udowodnij że n prostych na płaszczyźnie dzieli ją co najwyzej 2
n części.
24 lip 22:13
Mateusz:
w 2) zapomniałem dopisac ze a i b są liczbami wymiernymi
24 lip 22:15
5-latek: Zadanie . Podaj ktory z nasepujacych zbiorow jest skonczony ,pusty lub nieskonczony.
a)zbior liter alfabetu lacinskiego
b) zbior mieszkancow naszego miasta lu jesli ktos mieszka na wsi (tak jak ja ) to mieszkancow
nazej wsi
c) zbior licz podzielnych przez 10
d) zbior krokodyli w polskich rzekach
e) zbior pierwiastkow rownania x2=−16
f) zbior czarownic na Łysej Górze
g) zbior punktow na prostej.
Zadanie nr 2. tez z ebiorow
Czy moze byc A−B=A? lub taki zapis A\B=A
24 lip 22:22
Nie umiem matematyki: Dziękuje Za zadania . Teraz proszę o wstrzymanie sie w oddawaniu nowych . Jutro postaram sie je
wszystkie zrobić i dopiero wtedy poproszę o wiecej . Dzięki temu łatwo będziecie mogli
sprawdzać odpowiedzi. To mnie zmotywuje do pracy

24 lip 22:30
Mateusz:
Teraz co nie co z funkcji:
1) Ile jest roznych funkcji ze zbioru {1,2,3} w zbior {a,b,c,d}? Ile jest roznych funkcji
stałych z pierwszego zbioru w drugi?
2) Jesli funkcja f jest rosnąca w pewnym przedziale to jaka będzie w tym przedziale funkcja g
jesli g(x)=−f(x) rozpatrz problem na wybranym przez siebie przykładzie.
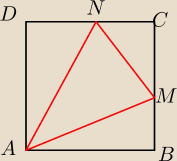
3) Kwadrat ABCD ma boki dlugosci 6cm na bokach BC i DC zaznaczono punkty M i N odpowiednio tak
że pola trójkątów ABM, MCN i ADN są równe znajdz długosci bokow BM i DN.
24 lip 22:32
Nie umiem matematyki: @Bezendu
Nie wiem jak to zrobić .
Wyszło mi ,ze równanie a
2=b
2+c jest prawdziwe dla
Liczb spełniających równanie

a+b=c gdzie a > b
25 lip 10:32
bezendu: pokaż jak zrobiłeś

25 lip 10:35
bezendu: a po drugie Ty masz podać konkretne liczby

25 lip 10:43
:/: a
2−b
2=c
| | (a−b)(a+b) | | (a+b) | |
(a+b)2= |
| * |
| |
| | a−b | | (a−b) | |
a − b = 1
b = a − 1
a
2=b
2+c
(1+b)
2 = b
2 +c
1 + 2b = c
1 + 2a − 2 = c
2b + 1 = c
2a − 1 = c

25 lip 11:35
imię lub nick: Pomoże mi ktoś czy nie?
25 lip 12:57
Piotr: Mila w tym zadaniu ''Wyznacz długość odcinka dwusiecznej kąta prostego w trójkącie
| | 24√2 | |
prostokątnym o przyprostokątnych 6cm, 8cm.'' Odpowiedź to: |
| ?  |
| | 7 | |
25 lip 13:22
Mila: Do Piotra, zgadza się.
Jaką metodą rozwiązałeś?
25 lip 13:31
;/: z twierdzenia o dwusiecznej w trójkącie + Pitagoras

25 lip 13:34
Piotr: Skorzystałem z dwóch twierdzeń znanych mi a mianowicie: ''Dwusieczna kąta trójkąta dzieli
przeciwległy bok na odcinku których stosunek długości jest równy stosunkowi długości
pozostałych boków.
Oraz z twierdzenia, ze w każdym trójkącie iloczyn długości dwóch boków jest równy kwadratowi
dwusiecznej kąta między nimi zawartego powiększonej o iloczyn odcinków, na które ta dwusieczna
podzieliła trzeci bok
Tego drugiego twierdzenia nigdy nie zapomnę

i oczywiście twierdzenie Pitagorasa jeszcze
wykorzystałem

25 lip 13:37
Piotr: @ ; / bez tego drugiego twierdzenia nie da rady rozwiązać

25 lip 13:38
Mila:
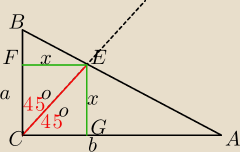
Pokażę inne sposoby.
I)
CGEF − kwadrat
ΔBFE∼ΔBCA⇒
xa=ab−bx
xa+xb=ab
x(a+b)=ab
II)
Z równoważności pól
| | 1 | | 1 | |
PΔACB= |
| *(a−x)*x+x2+ |
| *x*(b−x)= |
| | 2 | | 2 | |
| | 1 | | 1 | | 1 | |
=x2+ |
| *(ax−x2+bx−x2)=x2+ |
| (ax+bx−2x2)= |
| (ax+bx) |
| | 2 | | 2 | | 2 | |
porównuję pola
ax+bx=ab
x(a+b)=ab
25 lip 13:56
Piotr: Ja później przedstawię swój sposób rozwiązania, wieczorem jakoś

25 lip 14:07
Mila:
Twoje sposoby na pewno dobre, jednak chciałam pokazać, że można to rozwiązać bez podanych
twierdzeń.
25 lip 14:13
;/: a − b = 1
b = a − 1
a
2=b
2+c
(1+b)2 = b
2 +c
1 + 2b = c
1 + 2a − 2 = c
2b + 1 = c
2a − 1 = c
Już wiem ,
2b + 1 = c z tego wynika ,że c jest liczbą nie przystą
a−b=1 z tego że liczby a i b są liczbami sąsiadującymi.
| | c−1 | |
b = |
| <−− czyli b jest liczbą parzystą |
| | 2 | |
a = U{c+1{2} <−−−− a jest kolejną liczba parzystą po b
Musze więc podać liczby parzyste które są sąsiadujące .
tymi liczbami są 2,3
b = 2
a = 3
c = 5 <−−−− 2b+1 = c=5
Jest ! To znaczy prawie( a
2=b
2 −c) ale wierze ,że to tylko kwestia chęci sprawdzenia
obliczeń.

25 lip 14:13
;/: Mila , dziękuję za pokazania dwóch sposobów na rozwiązanie twojego zadania bez wzorów


Znasz może jakiś szybszy sposób na zadania przedstawione przez bezendu?
25 lip 14:21
ZKS:
Skoro a − b = 1 to ta sytuacja tylko zajdzie wtedy a oraz b będą kolejnymi liczbami dodatkowo
mają to być liczby pierwsze więc dostajemy od razu że jest to tylko spełnione
dla a = 3 oraz b = 2.
25 lip 14:36
Nie umiem matematyki: Tam mam zrobione , ale żeby równanie było prawidłowe b =3 a = 2
Czyli zrobiłem błąd wyprowadzajac rownanie a−b =1
25 lip 14:56
ZKS:
Ta i ciekawe jak dla b = 3 oraz a = 2 otrzymasz 2 − 3 = 1?
25 lip 15:02
ZKS:
Mając założenie że a > b wychodzi a = 3 oraz b = 2.
25 lip 15:03
:/: Ok dzięki.
Zaraz zabieram się za pozostałe.
25 lip 17:18
Nie umiem matematyki: W drugim mili wyszło mi 2−√3
25 lip 18:46
25 lip 19:07
Piotr: | | 2+√3 | |
Mila w tym drugim zadaniu nie powinien być taki stosunek |
| |
| | 2 | |
25 lip 21:13
Mila:
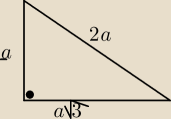
R=a
P
ko=πa
2
| | 1 | | 1 | |
p= |
| (a+2a+a√3)= |
| (3a+a√3) |
| | 2 | | 2 | |
| | a2√3 | | a*√3 | | a*(√3−1) | |
r= |
| = |
| = |
| |
| | a(3+√3) | | 3+√3 | | 2 | |
| | a2*(4−2√3) | | a2*(2−√3) | |
Pkw=πr2=π* |
| =π* |
| |
| | 4 | | 2 | |
| Pko | | 2 | |
| =(πa2)* |
| = |
| Pkw | | π*a2*(2−√3) | |
| | 2 | | 2*(2+√3) | |
= |
| = |
| =2*(2+√3) |
| | 2−√3 | | 4−3 | |
25 lip 22:44
Nie umiem matematyki: Dziękuje Ci Miła

{prezent}
25 lip 23:11
Mila: 
25 lip 23:11
Nie umiem matematyki: @Mila

25 lip 23:12
Mila:
Dziękuję. Powodzenia i sukcesów na miarę Vaxa.
25 lip 23:14
Piotr: Faktycznie
Mila ja odrazu użylem wzoru na promień tylko uzylem, ze r=a+b−c i nie
podzielilem przez 2 i dlatego zle mi wyszlo

26 lip 10:47
;/ : | | 1998*1999+2 | |
1) Czy |
| |
| | 1998)2+2000 | |
jest liczbą naturalną?
wiem ,że to równa się jeden ale jak to szybko rozwiązać ?
26 lip 12:29
ICSP: zauważyć że 2000 = 1998 + 2
26 lip 12:35
aniabb:
| 1998•(1998+1)+2 | | 19982+1998+2 | | 19982+2000 | |
| = |
| = |
| =1 |
| 19982+2000 | | 19982+2000 | | 19982+2000 | |
26 lip 12:37
ICSP: aniu 
26 lip 12:39
aniabb: 
już nie będę ..

ja tak odruchowo

26 lip 12:56
ICSP: zamiennik :
Pewna liczba sześciocyfrowa a kończy się cyfrą 5. Jeśli tę cyfrę przestawimy na
miejsce pierwsze ze strony lewej, to otrzymamy nowa liczbę, cztery razy większą od
poprzedniej. Znaleźć liczbę a.
26 lip 12:58
:/: 3) Udowodnij że n prostych na płaszczyźnie dzieli ją co najwyżej 2n części.
Proste najefektywniej dzielą płaszczyznę kiedy przecinają się w jednym punkcie .
Jeżeli liczba prostych wynosi 0 to płaszczyzna składa się z jednej części .
n ≥ 0
0 = 1
1 = 2
2 = 4
3 = 6
Z tego wynika ,że n prostych = 2n części . ehhh
wiem ,że tak jest ale nie potrafię tego do poprawnie zapisać.
Może mi ktoś wytłumaczyć jak to robić
26 lip 13:00
Mateusz:
aniabb "ti ti" nie rozwiązujemy zadan za kogoś

@ : / : własnie chodzi o to zeby rozwiązywac takie zadania jak 1) jak najprostszym sposobem bez
uzycia kalkulatora czyli cos zauwazyc dla potrenowania dam ci podobne:
| | 1*2*3*4*5*6*7*8*9*10 | |
sprawdz czy liczba: |
| jest całkowita |
| | (1*2*3*4)*(1*2*3*4*5*6) | |
co do zadania z prostymi jesli np wiesz co to jest indukcja matematyczna to mozna wykazac te
zaleznosc za jej pomocą co wymaga tez aby coś zauwazyc

jesli natomiast nie miałes
stycznosci z indukcją to takie uzasadnienie jak podałes w sumie wystarczy.
26 lip 13:54
ICSP: Mateusz tam na pewno jest znak * miedzy nawiasami ?
26 lip 15:55
Basia: a co ? za proste Ci się ICSP to zadanko wydaje ?
gdyby tam był + lub − liczba nie byłaby całkowita, więc pewnie jednak jest *
26 lip 16:33
26 lip 16:36
Basia:
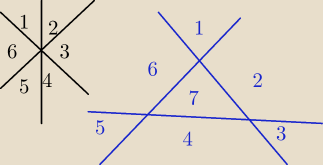
Co ma oznaczać to zdanie ?
Proste najefektywniej dzielą płaszczyznę kiedy przecinają się w jednym punkcie
Najefektywniej czyli na najwięcej części ?
Jeżeli tak, to jest to zdanie całkowicie
fałszywe.
Dowód na rysunku.
26 lip 16:42
Mateusz:
Tak ICSP jest tam znak mnozenia

i cicho tam siedziec nie podpowiadac
Tak masz racje Basiu jest to błąd, nie przeczytałem tego tylko zasugerowałem sie od razu
wynikami

26 lip 17:29
Basia: Witaj
Mateusz 
Samo twierdzenie oczywiście jest prawdziwe.
A co do tego zdania to zdaje się, że powinno być:
Proste dzielą płaszczyznę
na najmniejszą możliwą liczbę obszarów kiedy przecinają się w
jednym punkcie. Udowodnić, że wtedy jest tych obszarów 2
n to "mały pikuś".
26 lip 17:39
Basia:
P.S. oczywiście jeżeli są to różne proste
26 lip 17:41
Trochę umiem matematykę : : /
Narazie nie mam czasu.
26 lip 18:00
Trochę umiem matematykę : Przedtem robiłem wszystko pisząc z komórki teraz
Jak będę robił to z jakaś kartka. Teraz nie będę prosił was o pomoc xd
26 lip 18:02
Mateusz: Witaj witaj

Masz racje poniekąd widzisz ja to nie mam zdolnosci językowych chciałem sformułowac jak
najbardziej zrozumiale tresc tego zadania niestety o 22 tez czasami sie juz ciężko myśli

26 lip 18:03
Mila:
DO N.U.M albo T.U.M
Rozwiąż zadanie 1( z długością odcinka dwusiecznej) , korzystając z równoważności pól i wzoru
26 lip 18:05
Trochę umiem matematykę : @Mila Zrobiłem to przed chwilą na dwa sposoby .
W pierwszym sposobie użylem twierdzenie ,że w każdym trójkącie iloczyn dwóch boków jest równy
kwadratowi dwusiecznej kąta miedzy nimi zawartego powiekszonej o iloczyn odcinków ,na które ta
dwusiecznej podzieliła bok

W drugim zastosowaniem sie do twoich poleceń

Jutro pokaże obliczeniab bo jestem teraz na komórce .
Zauważyłem ze w drugim sposobie wyszedł ładny wynik
| | 1152 | |
Gdzie CD2= |
| i zauważyłem ze jeśli pomnożyć licznik i mianownik razy 2 |
| | 49 | |
To otrzymam ten ładny wynik

I teraz mam pytanie czy jest na to jakiś sposób ?(na otrzymywanie ładnych wyników

)
27 lip 00:10
Saizou : nie ma sposobu na otrzymywanie ładnych wyników, można jedynie się cieszyć jeśli takowe są

27 lip 00:13
;/ : | | 1*2*3*4*5*6*7*8*9*10 | |
sprawdz czy liczba: |
| |
| | (1*2*3*4)*(1*2*3*4*5*6) | |
jest całkowita.
Jak to rozwiązać ?
27 lip 13:07
pigor: 1) Wyznacz długość odcinka dwusiecznej kąta prostego w trójkącie prostokątnym o
przyprostokątnych 6cm, 8cm.
−−−−−−−−−−−−−−−−−−
to zadanie łatwo uogólnić na dowolny Δ i np. tu
dC= 2aba+b cos12C = 2*6*86+8cos45o= 482*12√2= 247√2.
27 lip 13:53
Mila:
Do
T.U.M
Zadanie 1.
Obojętne jaki sposobem rozwiązujesz wynik ma być ten sam:
Zastosowanie wzoru :
| | 1 | | √2 | |
PΔBCE= |
| *6*|CE|*sin45o=3*|CE|* |
| |
| | 2 | | 2 | |
| | 1 | | √2 | |
PΔACE= |
| *8*|CE|*sin45o=4*|CE|* |
| ⇔ |
| | 2 | | 2 | |
| | √2 | | √2 | |
3*|CE|* |
| +4*|CE|* |
| =24 |
| | 2 | | 2 | |
dokończ sobie
27 lip 15:38
Trochę umiem matematykę : @Mila Nie będę kończył bo juz wcześniej to zrobiłem :0
Tak przy okazji to ; / , TUM , NUM, imię lub nick to jedna osoba używam rożnych urządzeń
wszędzie mam inne pseudonimy, wcześniej uzywalem swojego imienia .
−−−−−−−−
Chociaż nie umieszczamy tutaj rozwiązań to staram sie rozwiązywać wszystkie zadania przez was
podane. Dzięki za zadania

27 lip 17:15
Mila: 
Jakie imię?
27 lip 18:12
Mateusz:
@ ; / ; jak to rozwiązac? Podobnie jak poprzednie trzeba coś zauwazyc i uzasadnic otrzymany
wynik

Mozna oczywiscie zastosowac podejscie brutalne czyli obliczyc wartosc tej liczby ale
nie o to tu chodzi

28 lip 17:36
5-latek: Zauwazyc np to ze 1*2*3*4*5*6=6!
28 lip 17:56
Mateusz:
Mozna ale nie trzeba

28 lip 19:13
ccc:
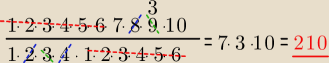
28 lip 19:20
Mateusz:
Widzisz
; / ; lubią cie wyręczać tu na forum

albo męczyc dostaniesz kolejne zadanie z
tej serii:
| | 2221564096+283748√462 | |
Czy liczba |
| jest wymierna? |
| | 491993569 | |
wskazówka skorzystaj z jednej z podstawowych własności tych liczb(broń boże nie wyliczaj jej
wartosci na kalkulatorze

)
28 lip 21:53
 Moj zakres to:
1. Dialania w zbiorach liczbowych
2. Wyrażenia algebraiczne
3. Geometria płaska−pojecia wstępne
4. Geometria płaska −trójkąty
5.Trygonometria
6.Geometria płaska −pole koła , pole trójkąta
7. Funkcja i jej własności
8.Przeksztalcenia wykresów funkcji.
Dziękuje
Moj zakres to:
1. Dialania w zbiorach liczbowych
2. Wyrażenia algebraiczne
3. Geometria płaska−pojecia wstępne
4. Geometria płaska −trójkąty
5.Trygonometria
6.Geometria płaska −pole koła , pole trójkąta
7. Funkcja i jej własności
8.Przeksztalcenia wykresów funkcji.
Dziękuje 



 Teraz co nie co z funkcji:
1) Ile jest roznych funkcji ze zbioru {1,2,3} w zbior {a,b,c,d}? Ile jest roznych funkcji
stałych z pierwszego zbioru w drugi?
2) Jesli funkcja f jest rosnąca w pewnym przedziale to jaka będzie w tym przedziale funkcja g
jesli g(x)=−f(x) rozpatrz problem na wybranym przez siebie przykładzie.
3) Kwadrat ABCD ma boki dlugosci 6cm na bokach BC i DC zaznaczono punkty M i N odpowiednio tak
że pola trójkątów ABM, MCN i ADN są równe znajdz długosci bokow BM i DN.
Teraz co nie co z funkcji:
1) Ile jest roznych funkcji ze zbioru {1,2,3} w zbior {a,b,c,d}? Ile jest roznych funkcji
stałych z pierwszego zbioru w drugi?
2) Jesli funkcja f jest rosnąca w pewnym przedziale to jaka będzie w tym przedziale funkcja g
jesli g(x)=−f(x) rozpatrz problem na wybranym przez siebie przykładzie.
3) Kwadrat ABCD ma boki dlugosci 6cm na bokach BC i DC zaznaczono punkty M i N odpowiednio tak
że pola trójkątów ABM, MCN i ADN są równe znajdz długosci bokow BM i DN.
 a+b=c gdzie a > b
a+b=c gdzie a > b





 i oczywiście twierdzenie Pitagorasa jeszcze
wykorzystałem
i oczywiście twierdzenie Pitagorasa jeszcze
wykorzystałem 

 Pokażę inne sposoby.
I)
CGEF − kwadrat
ΔBFE∼ΔBCA⇒
Pokażę inne sposoby.
I)
CGEF − kwadrat
ΔBFE∼ΔBCA⇒



 Znasz może jakiś szybszy sposób na zadania przedstawione przez bezendu?
Znasz może jakiś szybszy sposób na zadania przedstawione przez bezendu?

 R=a
Pko=πa2
R=a
Pko=πa2
 {prezent}
{prezent}




 już nie będę ..
już nie będę ..  ja tak odruchowo
ja tak odruchowo 
 @ : / : własnie chodzi o to zeby rozwiązywac takie zadania jak 1) jak najprostszym sposobem bez
uzycia kalkulatora czyli cos zauwazyc dla potrenowania dam ci podobne:
@ : / : własnie chodzi o to zeby rozwiązywac takie zadania jak 1) jak najprostszym sposobem bez
uzycia kalkulatora czyli cos zauwazyc dla potrenowania dam ci podobne:
 jesli natomiast nie miałes
stycznosci z indukcją to takie uzasadnienie jak podałes w sumie wystarczy.
jesli natomiast nie miałes
stycznosci z indukcją to takie uzasadnienie jak podałes w sumie wystarczy.
 Co ma oznaczać to zdanie ?
Proste najefektywniej dzielą płaszczyznę kiedy przecinają się w jednym punkcie
Najefektywniej czyli na najwięcej części ?
Jeżeli tak, to jest to zdanie całkowicie fałszywe.
Dowód na rysunku.
Co ma oznaczać to zdanie ?
Proste najefektywniej dzielą płaszczyznę kiedy przecinają się w jednym punkcie
Najefektywniej czyli na najwięcej części ?
Jeżeli tak, to jest to zdanie całkowicie fałszywe.
Dowód na rysunku.
 i cicho tam siedziec nie podpowiadac
Tak masz racje Basiu jest to błąd, nie przeczytałem tego tylko zasugerowałem sie od razu
wynikami
i cicho tam siedziec nie podpowiadac
Tak masz racje Basiu jest to błąd, nie przeczytałem tego tylko zasugerowałem sie od razu
wynikami 
 Samo twierdzenie oczywiście jest prawdziwe.
A co do tego zdania to zdaje się, że powinno być:
Proste dzielą płaszczyznę na najmniejszą możliwą liczbę obszarów kiedy przecinają się w
jednym punkcie. Udowodnić, że wtedy jest tych obszarów 2n to "mały pikuś".
Samo twierdzenie oczywiście jest prawdziwe.
A co do tego zdania to zdaje się, że powinno być:
Proste dzielą płaszczyznę na najmniejszą możliwą liczbę obszarów kiedy przecinają się w
jednym punkcie. Udowodnić, że wtedy jest tych obszarów 2n to "mały pikuś".
 Masz racje poniekąd widzisz ja to nie mam zdolnosci językowych chciałem sformułowac jak
najbardziej zrozumiale tresc tego zadania niestety o 22 tez czasami sie juz ciężko myśli
Masz racje poniekąd widzisz ja to nie mam zdolnosci językowych chciałem sformułowac jak
najbardziej zrozumiale tresc tego zadania niestety o 22 tez czasami sie juz ciężko myśli 
 W drugim zastosowaniem sie do twoich poleceń
W drugim zastosowaniem sie do twoich poleceń  Jutro pokaże obliczeniab bo jestem teraz na komórce .
Zauważyłem ze w drugim sposobie wyszedł ładny wynik
Jutro pokaże obliczeniab bo jestem teraz na komórce .
Zauważyłem ze w drugim sposobie wyszedł ładny wynik
 I teraz mam pytanie czy jest na to jakiś sposób ?(na otrzymywanie ładnych wyników
I teraz mam pytanie czy jest na to jakiś sposób ?(na otrzymywanie ładnych wyników  )
)


 Jakie imię?
Jakie imię?
 Mozna oczywiscie zastosowac podejscie brutalne czyli obliczyc wartosc tej liczby ale
nie o to tu chodzi
Mozna oczywiscie zastosowac podejscie brutalne czyli obliczyc wartosc tej liczby ale
nie o to tu chodzi 

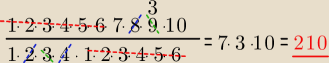
 albo męczyc dostaniesz kolejne zadanie z
tej serii:
albo męczyc dostaniesz kolejne zadanie z
tej serii:
 )
)