zadania Eta: Następna porcja zadań tylko dla przyszłych maturzystów zad.1/ Oblicz najmniejszą wartość wielomianu W(x)= (x−1)(x−2)(x−3)(x−4)+4 zad.2/ Wykaż,że liczba : 2012²+(2012*2013)²+2013² jest kwadratem liczby naturalnej zad.3/ Wykaż,że nie istnieją liczby dodatnie x,y,z,u spełniające równanie: (x+y√2)²+(z+u√2)² = 5+4√2 zad.4/ Wykaż,że jeśli liczby dodatnie x,y,z spełniają warunek x+y+z=3 to x²+y²+z²≥3 zad.5/ Wykaż,że jeśli liczby dodatnie x,y,z spełniają warunek xyz=1 to: x²+y²+z²+xy+yz+xz≥ 2(√x+√y+√z) powodzenia

ICSP: może podszyje się pod jakiegoś maturzystę i zrobię

Eta:

ICSP: anie jednego ?

Eta: Ani, ani

Eta: Pewnie chciałbyś zad1/ ? ...... ale na razie nie pozwalam

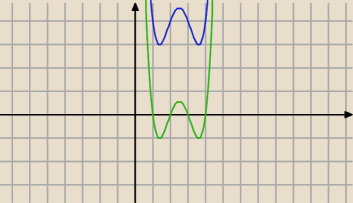
bezendu: najmniejsza wartość to 3 ?

ICSP: przygarne każde

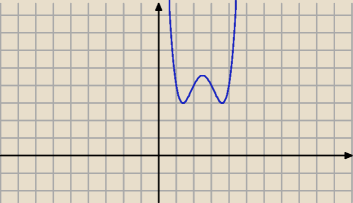
Eta: @bezendu wykaż, bez rysowania wykresu ( w którym zapewne pomógł Ci "wujek W.A"

bezendu: bez rysowania to trudno zrobić

Eta:

bezendu: ale najpierw ta funkcja (x−1)(x−2)(x−3)(x−4) a potem dopiero o 4 jednostki w górę

Eta: ciepło .......

ZKS: Trzeba mieć sposób na to zadanko powiem że ciekawe naprawdę.

Eta:

bezendu: jak to ciepło podałem już najmniejszą wartość 3

ZKS: A umiałbyś na maturze zrobić taki rysunek jaki Ci robi program?

bezendu: nie

bezendu: licealnym sposobem to raczej trudno to zrobić

Eta: No właśnie

bezendu: oj tam oj tam

Eta:

bezendu: Eta pamiętasz co mówiłem ''nie ładnie''

Eta: Żadne "oj tam" ... trzeba zdać maturę na 100%

bezendu: podstawową−czemu nie

Eta: Chodzi Ci o <jęzor>

bezendu: dokładnie chyba że tak smakował Ci obiad

Eta: Wrrr .... przepalone ziemniaki

bezendu: wyśle Ci kurierem to sobie odgrzejesz

Eta: Nie obijaj się .......... zadania czekają

ciuchcia: W(x) = (x − 1)(x − 2)(x − 3)(x − 4) + 4 = (x − 1)(x − 4)(x − 2)(x − 3) + 4 = (*) 1^o (x − 1)(x − 4) = x² − 4x − x + 4 = x² − 5x + 4 = x² − 5x + 5 − 1 2^o (x − 2)(x − 3) = x² − 3x − 2x + 6 = x² −5x + 6 = x² − 5x + 5 + 1 (*) = ( [x² − 5x + 5] − 1) ( [x² − 5x + 5] + 1) + 4 = ...

Eta: Ejjj ciuchcia z tego co pamiętam , to już jesteś po maturze !

bezendu: 5 wydaję się dość proste zaraz spróbuje zrobić

Trivial: Eta, mogę dać wskazówkę do pierwszego?

ciuchcia: a skądże

Eta: Ty Trivial ? zawsze

Eta: Ładnie tak kłamać ciuchcia ?

ZKS: To beznedu niech zrobi dla jakiego argumentu ta funkcja przyjmuje najmniejszą wartość.

Eta: O właśnie

bezendu: trudno określić dla jakiego

ZKS: To dam wskazówkę. Idąc dalej f(x) = [(x² − 5x + 5) − 1][(x² − 5x + 5) + 1] + 4 f(x) = (x² − 5x + 5)² − 1 + 4 f(x) = (x² − 5x)² + 2 * 5 * (x² − 5x) + 25 + 3 f(x) = (x² − 5x)² + 10(x² − 5x) + 28. Masz już jakiś pomysł?

bezendu: nie

ICSP: niech przyjmie t = (x² − 5x) i już gotowe praktycznie

Trivial: Ja tam taką wskazówkę. Zamiast rozważać W(x) łatwiej rozważyć W(x+2.5). Ponieważ nie interesuje nas x, wartość minimalna będzie taka sama.

Trivial: mam*

Eta:

bezendu: Eta jaka jest poprawna odpowiedź do zadania 1 ?

Trivial: bezendu: W(x) = (x−1)(x−2)(x−3)(x−4) + 4 W(x+2.5) = (x+1.5)(x+0.5)(x−0.5)(x−1.5) + 4 = (x²−2.25)(x²−0.25) + 4

ZKS: bezendu a jak myślisz? W(x) = (x² − 5x + 5)² + 3

Eta: No jasne,że tak

bezendu: 3

Eta: x_min=..........

Eta: No .... dawaj wynik

Trivial: Po wymnożeniu mamy: W(x+2.5) = x⁴ − 2.5x² + 4.5625

	Δ		6.25 − 18.25		−12
q = −		= −		= −		= 3.
	4a		4		4

bezendu: odpowiedź już była post 21:52

Eta: y_min= 3 dla x_min=.......... ?

bezendu: x≈4,41

Eta:

bezendu: to ja już dzisiaj nie wiem

Eta: x_min=.... v x_min=.....

Saizou : a to można zrobić za pomocą pochodnych

Eta: Nawet z rysunku ... (tak nie jest

bezendu: 1,3 lub 4,7

Eta: Nie ma pochodnych w programie dranie ...wyrzucili

Saizou : ale to aż się prosi o pochodne, a szkoda że nie ma

ZKS: W(x) = (x² − 5x)² + 10(x² − 5x) + 28 niech t = x² − 5x wtedy W(t) = t² + 10t + 28

	−10
tw =		= −5
	2

x² − 5x = −5 x² − 5x + 5 = 0 Δ = 5 √Δ = √5

	5 − √5
xmin1 =
	2

	5 + √5
xmin2 =		.
	2

bezendu: od kiedy pochodne są w lo chyba że jak ktoś sobie przerobi to ma

Saizou : bezendu rocznik 96 chyba na rozszerzeniu już będzie mieć pochodne

bezendu: dla mnie to oni nawet mogą mieć całki

Eta: ZKS łatwiej .......... y= (x²−5x+5)²+3 y= t²+3 , t= x²−5x+5 dla t=0 y_min=3 to x²−5x+5=0 ⇒ x_min= ... v x_min=....

Saizou : zad.1/ Oblicz najmniejszą wartość wielomianu W(x)= (x−1)(x−2)(x−3)(x−4)+4 W(x)=x⁴−10x³+35x²−50x+28 W'(x)=4x³−30x²+70x−50 W'(x)=0 4x³−30x²+70x−50=0 2x³−15x²+35x−25=0 2(2x−5)(x²−5x+5)=0

	5−√5		5		5+√5
↘ x1=		≈1,4 ↗ x2=		=2,5 ↘ x3=		≈3,6 ↗ (badając
	2		2		2

monotoniczność) i wystarczy teraz policzyć W(x₁) i W(x₃) i stwierdzić, która wartość jest najmniejsza

Trivial: Saizou, to ja już wolę sposób z liceum.

Eta: No i ....... jedno robaczywe które?

bezendu: 25 szans na prawidłową odpowiedź 3

ZKS: Jasne Eta że łatwiej i szybciej ale że ja już swoim jechałem sposobem i w końcu są wakacje to zrobiłem sobie wycieczkę z Polski do Hiszpanii przez Rosję.

bezendu: i chociaż coś zwiedziłeś i poznałeś nowe miejsca

Eta: O Ural też zachaczyłeś?

bezendu: a w Bajkale się kąpałeś

ciuchcia: bulu

ZKS:

martini: ja stawiam ze 4 jest robaczywe

Eta: Ejj bezendu nie zagaduj następne zadania czekają ( bo już więcej zadań...... nie będę na darmo pisać

bezendu: na jakie darmo ;> ostatnio jak prosiłem o zadania to prawie wszystkie zrobiłem

Eta: Ajjj zahaczyłeś

ciuchcia:

Eta: "bulu"

bezendu: https://matematykaszkolna.pl/forum/206290.html Eta przypomniało mi się zadanie 3 czeka na sprawdzenie ''na darmo mam pisać rozwiązanie''

Eta: ok

Saizou : zad.2/ Wykaż,że liczba : 20122+(2012*2013)2+20132 jest kwadratem liczby naturalnej 2012²+(2012*2013)²+2013²= (2013−2012)²+2*2013*2012+(2012*2013)²= 1+2*2012*2013+(2012*2013)²= (1+2012*2013)²

Eta: https://matematykaszkolna.pl/forum/208397.html zad 19 lipca 01:03 czeka na rozwiązanie

Eta: zad2/ brak jeszcze odp: że..........

bezendu: nie było mnie w tym temacie

Eta: Byłeś, byłeś

bezendu: ale to zadanie z planimetrii czyli sierpień a tymczasem już opuszczam forum

Saizou : 2012*2013 jest na pewno naturalne, bo jest to iloczyn dwóch liczb naturalnych dodatnich, powiększony o 1 jest dalej liczbą naturalną

Eta:

zxcv: Zad4 Wiadomo, że x² +y² +z² ≥ xy + yz + zx mnożymy obustronnie razy 2 i dodajemy obustronnie x² +y² +z² 3*(x² +y² +z²) ≥ x² +y² +z² + 2(xy + yz + zx) ⇔ 3*(x² +y² +z²)≥ (x² +y² +z²)² ⇔ 3*(x² +y² +z²)≥ 9 ⇔ x² +y² +z²≥ 3

Eta: Wrócę do tego zadania .... po wakacjach

zxcv: tam po prawej stronie ma być (x+y+z)² a nie (x² +y² +z²)²

ZKS: Zadanie 2. 2012² + (2012 * 2013)² + 2013² = (2012² + 2012 + 1)². Idę od razu żeby nie dostać.

Eta: ok

Eta: Dostajesz

Eta: "101 dalmatyńczyków" moje

ZKS: A ja mam "RUDY 102".

ZKS: A jednak nie. To było 103.

Eta: 103 −−−− liczba pierwsza

ZKS: Eta czy w Twoim zadaniu "https://matematykaszkolna.pl/forum/208397.html zad 19 lipca 01:03 czeka na rozwiązanie" pole tego trapezu wynosi 4√3?

Eta: Dokładnie tak

Eta: Nie podawaj rozwiązania niech maturzyści myślą

ZKS: Dlatego właśnie spytałem tylko o wynik. W takim razie dziękuję bardzo. i dla Ciebie.

Eta: Hej Godzio Pamiętasz zmagania z tym zadaniem z trapezem?

Godzio: Hejo Widzę, że nie można pozostać anonimowym Pamiętam, pamiętam Ale w końcu nie wymyśliłem najprostszego rozwiązania

Eta:

Godzio: ZKS mam dla Ciebie coś ambitniejszego Udowodnij, że liczba p jest pierwsza tylko wtedy gdy (p − 1)! + 1 jest podzielne przez p.

Eta: Ciekawe co wymyśli ....... Saizou

Eta: "coś ambitniejszego?

Godzio: Niż zadania maturalne

Eta:

Godzio: To ilu mamy tutaj maturzystów Saizou i bezendu, ktoś jeszcze ?

ZKS: Coś mi się obiło o uszy to zadanie z Twierdzeniem Wilsona. Piotr jest jeszcze.

Godzio: To jest twierdzenie Wilsona

ZKS: No coś tam słyszałem właśnie.

fx: Ja też maturzysta... Choć nie pierwszy raz, przyznać muszę.

ICSP: a ja we wrześniu zapisze się na poprawkę matury Tzn że też będę maturzystą i mogę robić zadanka

Godzio: To może ja też, bo w sumie matura mi do dupy poszła ?

ICSP: Eta możesz dawać zadania Mamy dwóch nowych maturzystów

ZKS: To i ja może się zgłoszę na korepetycje do kogoś to sobie też napiszę maturkę.

ciuchcia: macie mój miecz! (jeszcze potrzebujemy łuk i topór)

ICSP: ja będę przewodnikiem

ciuchcia: powiernik pierścienia

ICSP: chyba bardziej były właściciel

fx: Myślałem, że napisanie maturki z matmy R mając za sobą już trzy semestry matematyki wyższej to będzie hop . Jakoś tak mi mina rzewnie co otwieram zbiorek Kiełbasy... Znaczy się muszę sobie przypominać licealne metody ze szkolnej ławy.

Saizou : 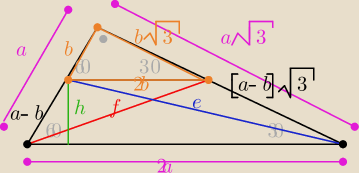Zadanie W trapezie o kątach ostrych 30^o i 60^o, zaś różnica kwadratów przekątnych trapezu wynosi 16 Oblicz pole tego trapezu. e>f e²−f²=16 z tw. Pitagorasa a²+3b²=f² b²+3a²=e² b²+3a²−a²−3b²=16 2a²−2b²=16 a²−b²=8

	h
sin60=
	a−b

√3		h
	=
2		(a−b)

	√3(a−b)
h=
	2

	(2a+2b)*h		(a−b)√3		(a2−b2)√3		8√3
P=		=(a+b)*h=(a+b)*		=		=		=4√3
	2		2		2		2

Trivial: fx, przecież na maturze dowolna metoda jest poprawna − czyli możesz sobie rozwiązywać zadania nawet przy pomocy jakiejś geometrii eliptycznej czy innych całek Lebesgue'a. Jeśli będzie poprawne rozwiązanie muszą uznać.

Saizou : a jakie jest najprostsze rozwiązanie tego zadania ?

ZKS: Nikt jeszcze nie znalazł tego najprostszego rozwiązania tylko Bogdan wie.

Eta: Ładnie Saizou 2 sposób ( rys. ten sam) : : a²−b²=8 teraz: P_tr= P(Δ dużego) − P(Δ małego)

	a2√3		b2√3		√3		√3
Ptr=		−		=		(a2−b2)=		*8= 4√3 [j2]
	2		2		2		2

Saizou : tak jak na początku patrzyłem na zadanie to mi się wydawało za mało danych, ale dałem radę

Mila: ZKS− znalazł, ale nie napisał.

Eta:

Eta: zad .6/ Wielomian W(x)=x²⁰¹³+ax²⁰¹¹+bx²⁰⁰⁹ +cx+6 jest podzielny przez x²+x+1 Wyznacz resztę z dzielenia wielomianu W(x) przez x²−x+1

Eta: Łap zadanie Saizou

Saizou : zobaczymy co da się zrobić, na razie kombinuję nad zadaniem 5 i mam że x²+y²+z²+xy+xz+yz≥0

Saizou : zad.5/ Wykaż,że jeśli liczby dodatnie x,y,z spełniają warunek xyz=1 to: x²+y²+z²+xy+yz+xz≥ 2(√x+√y+√z) Prawdą jest że (x+y)²≥0 (x+z)²≥0 (y+z)²≥0 + 4(√a+√b+√c)≥0 − −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− = 2(x²+y²+z²)+2(xy+xz+yz)−4(√x+√y+√x)≥0 x²+y²+z²+xy+xz+yz≥2(√x+√y+√x) cnu

ICSP: prawdą jest że : 1 > 0 −1 > −3 zatem odejmując stronami prawda jest żę : 2 > 3 brawo Saizou brawo

Eta: 2 sposób z nierówności między średnimi am−gm x²+yz≥2√x²yz = 2√x*(xyz)= 2√x , bo xyz=1 : : +−−−−−−−−−−−−−−−−−−−−−−−− x²+y²+z²+xy+xz+zy ≥ 2√x+2√y+2√z = 2(√x+√y+√z)

Saizou : ICSP liczby a,b,c są dodatnie

Eta:

Eta: ICSP

ICSP: 2> 0 3 > 0 odejmując −1 > 0

Eta: xyz=1

Saizou : i cały mój dowodzić poszedł sobie w siną dal

ZKS: Prawie identyczny sposób który pokazała Eta. (x − √yz)² ≥ 0 (y − √xz)² ≥ 0 (z − √xy)² ≥ 0 dodajemy stronami te nierówności i otrzymujemy x² − 2x√yz + yz + y² − 2y√xz + xz + z² − 2z√xy + xy ≥ 0 x² + y² + z² + xy + xz + yz − 2(√x²yz + √xy²z + √xyz²) ≥ 0 skoro xyz = 1 to x² + y² + z² + xy + xz + yz − 2(√x + √y + √z) ≥ 0 x² + y² + z² + xy + xz + yz ≥ 2(√x + √y + √z)

Eta:

ZKS: Eta czy w Twoim zadaniu z wielomianem reszta to 12?

Eta:

ZKS: Chyba się skuszę na poprawę matury haha.

Eta:

ZKS: Rozwiązania nie piszę żeby nie psuć zabawy Saizou.

Eta: Pamiętasz co radził Ci Godzio? .... "coś ambitniejszego"

Eta: Nie pisz ....... poczekamy na przyszłych maturzystów

ZKS: Ale to z wielomianem było ambitne robi się szybko ale trzeba pomyśleć. Tak jak Godzio da mi coś ambitniejszego to będę musiał szczękę z podłogi podnosić. Już nie mam matematyki na studiach skończyło się dopiero po inżynierce na magisterce będę znowu miał.

Godzio: No to tym bardziej powinieneś cisnąć, żeby nie zapomnieć

ZKS: Oooo nie! Muszę uciekać.

ZKS: To może żeby nie zapomnieć matematyki porobię sobie testy maturalne.

Godzio: Za proste

Saizou : zad.4/ Wykaż,że jeśli liczby dodatnie x,y,z spełniają warunek x+y+z=3 to x²+y²+z²≥3 z zależności między średnią kwadratową, a arytmetyczną

	a2+b2+c2		a+b+c
√		≥
	3		3

	a2+b2+c2
√		≥1 , bo a+b+c=3
	3

a2+b2+c2
	≥1
3

a²+b²+c²≥3 ale zapewne coś popsułem

ZKS: Saizou dobrze właśnie najlepiej jest wykorzystywać zależności między średnimi. Mam jeszcze inny nieco dłuższy sposób. z = 3 − x − y x² + y² + (3 − x − y)² ≥ 3 x² + y² + 9 + x² + y² − 6x − 6y + 2xy − 3 ≥ 0 2x² + 2y² − 6x − 6y + 2xy + 6 ≥ 0 x² + (y − 3)x + y² − 3y + 3 ≥ 0 Δ_x = (y − 3)² − 4(y² − 3y + 3) = y² − 6y + 9 − 4y² + 12y − 12 = −3y² + 6y − 3 = −3(y² − 2y + 1) = −3(y − 1)² ⇒ Δ ≤ 0 Brak miejsc zerowych albo jedno zatem wyjściowa nierówność x² + y² + z² ≥ 3 jest spełniona. I z poziomu studiów. Tworzymy funkcję Lagrange'a F(x ; y ; z ; λ) = x² + y² + z² + λ(x + y + z − 3) F'_x = 2x + λ F'_y = 2y + λ F'_z = 2z + λ {2x + λ = 0 {2y + λ = 0 {2z + λ = 0 {x + y + z − 3 Rozwiązując ten układ otrzymujemy że λ = −2 ∧ x = y = z = 1 zatem najmniejsza wartość funkcji będzie dla x = y = z = 1 F(x ; y ; z) = x² + y² + z² F(1 ; 1 ; 1) = 1² + 1² + 1² = 3

Saizou : zad.3/ Wykaż,że nie istnieją liczby dodatnie x,y,z,u spełniające równanie: (x+y√2)²+(z+u√2)² = 5+4√2 niech x+y√2=a a>0 z+u√2=b b>0 a²+b²=5+4√2 (a+b)²−2ab=(2+√2)²−1 ll V a+b=2+√2 i 2ab=1 2√ab=√2 bo a,b>0 a+b+2√ab= 3+√2

	1		3
(√a+√b)2=(		+√2)2+
	2		4

wiec nie istnieją takie liczby a oraz b żeby równanie było prawdziwe, zatem nie ma takich liczb x,y,z,u spełniających równanie (x+y√2)²+(z+u√2)² = 5+4√2

Eta:

Saizou : yyyyyyy.........czyli to jest dobrze

Godzio: Jak dla mnie nie można sobie tak uprościć, bo równie dobrze może być a + b = − (2 + √2)

Saizou : Godzio liczby a,b>0 a suma liczb dodatnich nie może być ujemna

Godzio: No to inaczej (1 + 1)² + 2 * 1 * 1 = (0.5 + 0.5)² + 5 A wcale z tego nie wynika, że 1 + 1 = 0.5 + 0.5 i 2 * 1 * 1 = 5

Saizou : eh........... kolejny dowód zepsuty trzeba by się ogarnąć

Godzio: Wsk. Z faktu, że 2√2 + 1 = a√2 + a + b wynika, że 2 = a i a + b = 1 Nie wiem czy to użyteczne, ale ja bym tak próbował na początek

Eta: Tak, Saizou ... niestety,ale zadanie "skopane" !

bezendu: Eta mam do Ciebie pytanie ?

Eta: Pytaj

bezendu: Pamiętasz jak podawałaś ten wzór ''trapez−Eta'' ? Tego wzoru nie ma w tablicach więc jeśli chcę go użyć na maturze to muszę go wyprowadzić ?

Eta: Dla pewności, wypadałoby ten wzór wyprowadzić (a dowód nie jest trudny

bezendu: Właśnie chodziło mi to czy wyprowadzać, czy nie jest dużo takich wzorów których nie ma w tablicach a istnieją

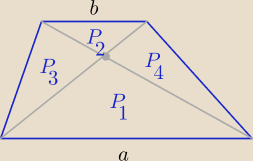
Eta: P₃= P₄ (wiesz.... P(tr)= P₁+P₃+P₄+P₂= P₁+2P₃+P₂ = (√P₁+√P₂)² gdzie P₃=P₄=√P₁*P₂ i tyle

	a
lub taki wzór Ptr= (k+1)2*P2 , k=		>0 −− skala podobieństwa trójkątów o polach P1
	b

i P₂

	P1
to		= k2 i P3=P4= k*P2
	P2

P_tr= P₁+2P₃+P₂= k²*P₂+2k*P₂+P₂ = P₂(k²+2k+1)= (k+1)²*P₂

bezendu: Dziękuje choć sam też bym chyba sobie poradził

Eta: Wiem,wiem chciałam Ci tylko przypomnieć,że dowód nie jest trudny .