zadania
Eta: Wakacyjne
"łamanie głowy" ....... trening dla przyszłych
maturzystów  Zad.1/
Zad.1/
Dany jest trójkąt równoramienny o podstawie długości "
a" i ramionach długości "
b"
oraz kącie między ramionami
20o
Wykaż,że spełniona jest równość :
a3+b3=3ab2
zad.2/
Wykaż,że zachodzi równość: tg
236
o*tg
272
o=5
zad.3/
Jeżeli a,b>0 i a
2+b
2=10ab
| | a−b | |
Oblicz wartość W= |
| |
| | a+b | |
zad.4/
W trapezie ABCD , AB II CD .Wiedząc,że |AD|=DC| i |AC|=|BC| i |AB|=DC|+|BC|
Oblicz miary kątów tego trapezu
zad.5/
W [P[n]−kątnym wielokącie wypukłym liczba boków i liczba przekątnych są liczbami
nieparzystymi. Wykaż ,że liczba
n−1 jest podzielna przez
4
zad.6/
Kąty A, B, C są ostre i takie,że A+B+C= 90
o
| | A+B | | A+C | | B+C | |
Wykaż,że cosA+cosB+cosC= 4cos |
| *cos |
| *cos |
| |
| | 2 | | 2 | | 2 | |
Pozdrawiam i powodzenia
maturzyści 

16 lip 22:26
ZKS:
Hehe jak specjalnie zaznaczone dla
maturzystów.

16 lip 22:35
Dominik: mam jedno proste, ale ciekawe (przynajmniej w moim mniemaniu) zadanko. rozwazmy okregi O1 i
O2 o srodkach odpowiednio w punktach S1 i S2 i promieniach r1 i r2. nalezy udowodnic, ze
sa rozlaczne, gdy r1 + r2 < |S1S2|. powodzenia maturzysci.
16 lip 22:41
ICSP: zad,7/
Pewna liczba sześciocyfrowa a kończy się cyfrą 5. Jeśli tę cyfrę przestawimy na
miejsce pierwsze ze strony lewej, to otrzymamy nowa liczbę, cztery razy większą od
poprzedniej. Znaleźć liczbę a.
16 lip 22:44
Piotr: Zadanie 3
W(a+b)=a−b * ()
2
W
2(a+b)
2=(a−b)
2
W
2(a
2+2ab+b
2)a
2−2ab+b
2
W
2(12ab)=8ab
Hmm ?
16 lip 22:47
Piotr: Nie wiem czy do kwadratu mogę w ogole podniesc

16 lip 22:48
ICSP: co do zadania
Dominika biorę :
o
1 : (x−3)
2 + (y−2)
2 = 100
o
2 : (x−7)
2 + (y−2)
2 = 4
|S
1S
2| = 4
r
1 + r
2 = 12
12 < 4

Okręgi są oczywiście rozłączne.
16 lip 22:48
ICSP: Oczywiście zadanie jest dla maturzystów

Ja tylko próbuje wskazać błą w treści a nie je rozwiązywać

16 lip 22:50
Piotr: @ICSP mozesz spojrzec na moje rozwiazanie zadania 3

?
16 lip 22:51
Dominik: oczywiscie chodzilo o rozlaczne zewnetrznie, przez nieuwage zapomnialem. chwali sie
wynajdowanie takich bledow.

16 lip 22:51
ZKS:
Piotr wynik dobry.

16 lip 22:52
Piotr: @ZKS tylko z tym kwadratem nie pewny nadal jestem, nie wiem czemu

. Bo na przyklad prawa
strona moze byc ujemna. Nie wiadomo czy obie strony sa dodatnie
16 lip 22:53
ZKS:
Tutaj masz tylko obliczyć wartość a nie rozwiązywać równanie więc w tym wypadku można
podnieść do kwadratu.
Identyczne są zadania przykładowo
należy obliczyć wartość sin(x)cos(x) tutaj tak samo podnosimy do kwadratu obustronnie
więc ja bym Ci uznał to zadanie z max ilością punktów ale lepiej niech się inni wypowiedzą.
16 lip 22:57
Dominik: takze ISCP, mam nadzieje, ze bledow wiecej nie ma. nie jestem zbytnio doswiadczony w wymyslaniu
zadan i takie drobne niunse moga mi uciec. jesli jest OK zostawmy je maturzystom.

16 lip 22:58
Piotr: Ok, dzięki

16 lip 22:59
ZKS:
Zadanie to można zrobić w inny ale dłuższy od Twojego sposobu jeżeli masz wątpliwości.
Skoro wiemy że a
2 + b
2 = 10ab to
a
2 − 10ab + 25b
2 − 24b
2 = 0
(a − 5b)
2 − (2
√6b)
2 = 0
(a − 5b − 2
√6b)(a − 5b + 2
√6b) = 0
Dla a = 5b + 2
√6b
| | 5b + 2√6b − b | | √6 | |
W = |
| = |
| |
| | 5b + 2√6 + b | | 3 | |
dla a = 5b − 2
√6b
| | 5b − 2√6b − b | | √6 | |
W = |
| = − |
| . |
| | 5b − 2√6b + b | | 3 | |
Teraz wszystko jasne?

16 lip 23:04
Piotr: Tak, jasne

. Wpaść na Twój pomysł to huhu

16 lip 23:06
Eta:
zad3/ Można też tak:
a2+b2= (a+b)2−2ab ⇒(a+b)2= 12ab ⇒|a+b|= 2√3ab
i a2+b2= (a−b)2+2ab ⇒(a−b)2= 8ab ⇒|a−b| = 2√2ab
W=.......
16 lip 23:08
ZKS:
Właśnie o to chodzi w matematyce że jest wiele sposobów na rozwiązanie zadanie ale trzeba
dostać zawsze ten sam poprawny wynik.

16 lip 23:12
Eta:

16 lip 23:13
Piotr: Wiem, tutaj już są 3 sposoby a na pewno jest ich jeszcze z kilka. Na razie męczę się z 1
zadaniem

16 lip 23:14
Eta:
Męcz się męcz

aż do skutku

16 lip 23:15
Piotr: Eta zadanie 1 coś tw. kosinusów lub sinusów

? Czy inna bajka ?
16 lip 23:16
Eta:
sin3α=......
16 lip 23:20
Piotr: Aż tak nie ogarniam trygonometrii, w szkole nie miałem jeszcze sin2α(funkcji sumy i różnicy)
itd choć mnie to i tak nie usprawiedliwia
16 lip 23:22
16 lip 23:25
Piotr: No okej mam ten wzorek, tylko nie wiem kompletnie jak on ma się do tego zadania
16 lip 23:27
ZKS:
Dam jedno zadanie z wielomianów.
Rozwiązać równanie:
(x + 1)(x + 3)(x − 2)(x − 6) − 91x2 = 0.
16 lip 23:28
Eta:
Na razie myśl

zapisz sin10
o=.... (z trójkąta
i sin30
o =...
i już prawie ........

16 lip 23:29
Piotr: Widzę
ZKS nadal te równanko nie rozwiązane

16 lip 23:30
Eta:
Hej
ZKS ....... niedawno było to zadanie

16 lip 23:30
Eta:
zad.
ZKS:
(x
2+8x−6)(x
2−12x+6)=0

x=.........
16 lip 23:34
ZKS:
Eta bardziej chodzi mi o sposób.

Jak doprowadziłaś do dwóch nawiasów nie to że Cie
chcę sprawdzić ale czy tym najłatwiejszym sposobem to zrobiłaś.

Przepraszam za natręctwo.

16 lip 23:37
ZKS:
Malutki chochlik się wtrącił
(x
2 + 8x − 6)(x
2 − 12x
− 6) = 0.

16 lip 23:39
Piotr: Zadanie 1
Doszedlem do takiego czegoś:
16 lip 23:41
Eta:
No i ładnie

| 3ab2−a3 | | 1 | |
| = sin3*10o= |
| |
| 2b3 | | 2 | |
dokończ.......
16 lip 23:54
Piotr: 3ab
2−a
3=b
3
a
3+b
3=3ab
2 c.n.u

16 lip 23:57
Piotr: Tak naprawdę to pierwszy raz w życiu użyłem tego wzoru sin3α

17 lip 00:01
Marque: Eta jak Ty to robisz, ze pykasz sobie kazde zadanko? Zdradz sekret tak trwalej i skutecznej
nauki matematyki. Za 300 dni matura, a ja widze u siebie duze braki

17 lip 00:03
Piotr: Ja na przykład robię zadania różnego rodzaju, te zadania co
Eta daję to są trudne , ale
uczą myślenia

17 lip 00:06
Eta:
Hehe

Rozwiązuj zadania ....światek, piątek i niedziele
i tak "do końca świata i jeszcze jeden dzień dłużej"

17 lip 00:06
Eta:
@
Piotra
I co? ... trudne było?

17 lip 00:08
Piotr: Nie było

. Teraz łatwe, tylko nie znałem wzoru sin3α, bo co prawda miałem trygonometrię w I
klasie, ale teraz w III klasie będę miał sin2α itd

. Zadanie 3 też jakoś z tych wzorów czy
nie?

17 lip 00:09
Piotr: Przepraszam, zadanie 2 jak coś

17 lip 00:10
Eta:
zad2. na razie odpuść ( rozwiążesz je, jak pouczysz się szerzej trygonometrii)
17 lip 00:12
Eta:
Zad.4/ ( łatwe

narysuj trapez i ........
17 lip 00:14
Piotr: Ok. Widzę, że zadanie 6 też nie zrobię. Nad zadaniem 4 dzisiaj wieczorem pomyślę, bo tutaj
trzeba dobry rysunek zrobić, ale jakoś nie chce mi wyjść. Dziękuję
Eta za pomoc


17 lip 00:15
Eta:
Miłych snów ....... do jutra

17 lip 00:16
Piotr: Dzięki i wzajemnie


17 lip 00:17
Eta:
zad.5/ ma być : W n−kątnym
17 lip 00:17
Saizou :
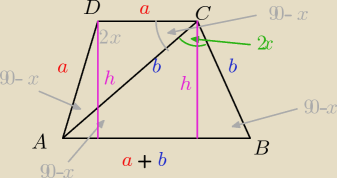
a*sin(2x)=h
bcos(x)=h
a*sin(2x)=b*cos(x)
2sin(x)cos(x)*a=bcos(x) bo x∊(0:90)
2sin(x)*a=b
| | 1 | | 1 | | 1 | |
Pt= |
| a2*sin(2x)+ |
| b2*sin(2x)= |
| sin(2x)(a2+b2) |
| | 2 | | 2 | | 2 | |
| (2a+b)*a*sin(2x) | | 1 | |
| = |
| sin(2x)(a2+b2) |
| 2 | | 2 | |
(2a+b)*a*sin(2x)=sin(2x)(a
2+b
2)
2a
2+ab=a
2+b
2
a
2+ab−b
2=0 : a
2
| | b | | b | | b | |
1+ |
| −( |
| )2=0 |
| =t t>0 |
| | a | | a | | a | |
−t
2+t+1=0
Δ=1+4=5
√Δ=
√5
| | −1+√5 | | 1−√5 | |
t2= |
| = |
| sprzeczność |
| | −2 | | 2 | |
no i teraz nie wiem jak policzyć dokładną wartość x

17 lip 11:52
ICSP: policz cosx
17 lip 12:02
Saizou : | | 1+√5 | |
sinx= |
| ≈0,8090→x=54o czy tak by wystarczyło czy trzeba liczyć jakoś dokładną |
| | 4 | |
wartość

17 lip 12:03
Eta:
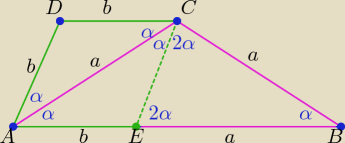
Hej
Saizou 
Taki rys. wystarczy?

17 lip 12:46
Saizou : witaj Eta
a co z moim sposobem rozwiązania?
17 lip 12:49
AS: W zadaniu 1) nie rozumiem po co jest dany
kąt między ramionami = 20o.
Przecież podane a i b określają jednoznacznie
trójkąt i to jeden.
17 lip 13:00
Piotr: @AS właśnie przydał się ten kąt gdyż jak poprowadzisz wysokość to kąt podzieli sie na polowe i
otrzymasz dwa trojkaty prostokatne
17 lip 13:04
Piotr: Zadanie 5
| n(n−3) | |
| <== wzór na ilość przekątnych w wielokącie; jest to liczba nieparzysta( z |
| 2 | |
założenia)
n <== liczba boków w wielokącie; jest to liczba nieparzysta( z założenia)
n−3 musi być podzielne przez 2
n−3 nie może być podzielne przez 4, gdyż n jest liczbą nieparzystą
Gdy n−3 podzielimy przez 4 otrzymamy resztę 1.
Resztę 3 odrzucam, ponieważ liczba (n−3) będzie podzielna przez 4.
Reasumując: n=4p+1, gdzie p∊C 4p=n−1 c.n.u
17 lip 13:57
Saizou : Eta a w tym moim rozwiązaniu jest gdzieś błąd

17 lip 22:36
Saizou : Czy ktokolwiek mógłby odpowiedzieć na moje pytanie

czy w moim rozwiązaniu zadania z trapezem jest gdzieś błąd

17 lip 23:33
Eta:
Hej
Saizou
| | 1+√5 | |
złota liczba |
| jest dokładną wartością cos36o |
| | 4 | |
Poszukaj błędu lub jak radzi
ICSP zastosuj cosα
Nie chce mi się w tej "dżungli amazońskiej" szukać błędu, boję się krokodyli

17 lip 23:47
Saizou : cos36
o=sin(90−54)=sin54
o 
<−−−− czy ja coś źle myślę

ale to dżungla bez krokodyli i wszystkich innych stworzonek i niebezpiecznych roślin

17 lip 23:51
Eta:
Zastanawiam się ......... czemu uparłeś się na takie rozwiązanie?
Z rys. w trójkącie ABC : 5α=180
o ⇒
α= 36o
i pozostałe miary kątów podajesz już bez problemu

17 lip 23:52
Saizou : no bo takie mi pierwsze do głowy przyszło xd wiec warto wiedzieć jak je rozwiązać do końca
17 lip 23:53
17 lip 23:55
Eta:
Czyli ok

ale musisz wykazać,że to dokładna wartość
a nie jak napisałeś ≈ 54
o
17 lip 23:57
Eta:
Tak, tak

( pomyłkowo wpisałam
17 lip 23:58
Saizou : | | 1+√5 | |
a czy bazując na wiedzy że przybliżona wartość kąta ≈54o mogę pokazać, ze sin54o= |
| |
| | 4 | |

17 lip 23:59
Eta:
I wszystko jest ok

( bo nie spojrzałam na oznaczenia na Twoim rys.
18 lip 00:00
Saizou : czyli i tak trzeba wyliczyć wartość sin(54) ?
18 lip 00:01
Eta:
Tak

18 lip 00:02
Eta:
| | 1+√5 | | 1+√5 | |
Dopisujesz tak: cos36o= |
| ⇒ sin54o= |
| |
| | 4 | | 4 | |
18 lip 00:05
Saizou : i co mi to da, bo jakoś nie myślę już o tej porze

18 lip 00:06
Eta:
Jak to co? ( na Twoim rysunku)
<B= 36o <A= 2*36o <C= ... .. <D= .......
Kwestionowałam Twoją odp: 54o (dlatego,że nie spojrzałam na oznaczenia na Twoim rys)
Zasugerowałam się oznaczeniami katów z mojego rys.
18 lip 00:10
Saizou : | | 1+√5 | |
nic się nie stało, bo cały czas myślałem że muszę udowodnić że sin54= |
| , ale jak nie |
| | 4 | |
trzeba to resztę ogarniam jak najbardziej

18 lip 00:12
Eta:
Tak naprawdę wypadałoby to udowodnić.......
lub napisać,że ta wartość jest Ci znana ! (jak 2*2=4

18 lip 00:14
Saizou : to dziękuję za rozwianie moich wątpliwości, postaram się jutro udowodnić tego sinusa

18 lip 00:17
Eta:

18 lip 00:19
Eta:
Jutro wrzucę kilka zadań z
planimetrii 
Miłych snów

18 lip 00:23
Saizou : planimetria nawet się przyjemna zrobiła

i również
kolorowych
18 lip 00:28
bezendu: To znaczy w piątek?

18 lip 00:44
Saizou : bezendu przebywam właśnie w Hiszpanii i jeszcze mamy środę

(dżołk)
18 lip 00:46
Saizou : sin54=cos36
sin(3*18)=cos(2*18)
3sin18−4sin
318=1−2sin
218
4sin
318−2sin
218−3sin18+1=0 sin18=t t∊(0:1)
4t
3−2t
2−3t+1=0
(t−1)(4t
2+2t−1)=0
4t
2+2t−1=0 lub t=1 (sprzeczność)
Δ=4+16=20
√Δ=2
√5
| | −2−2√5 | | −1−√5 | |
t1= |
| = |
| sprzeczność |
| | 8 | | 4 | |
| | √5−1 | | √5−1 | |
sin(54)=sin(3*18)=3* |
| −4*( |
| )3=...(tutaj rachunki, ale nie chce mi się |
| | 4 | | 4 | |
18 lip 20:56
Eta:
No i pięknie

19 lip 00:40
Eta:
Krokodyle Cię nie zjadły
Saizu ?

19 lip 00:41
Saizou : Eta a nawet gdyby zjadły to nabawiłyby się niestrawności

19 lip 01:00
Eta:

19 lip 01:00
ciuchcia: zapewne takie rozwiązanie byłoby jako nr 1 w schemacie oceniania na maturze

19 lip 01:03
Eta:
No to takie zadanko

W trapezie o kątach ostrych 30
o i 60
o, zaś różnica kwadratów przekątnych trapezu wynosi 16
Oblicz pole tego trapezu.
19 lip 01:03
ICSP: Fajna treść

Tak spójnia

19 lip 01:08
Eta:
Miało być bez słwoa"zaś"

19 lip 01:10
Eta:


19 lip 01:12
Eta:

19 lip 01:17
ciuchcia: 
19 lip 01:18
5-latek: No to zadanie z planimetrii
Udowodnic ze jezeli trojkat ma os symetrii to jest rownoramienny >
20 lip 16:13
5-latek: I jeszcze jedno zadanie
W plaszcyznie trojkata rownobocznego ABC o boku dlugosci a znalezc pole obszaru zawierajacego
takie i tylko takie punkty M ze:
a) Katy AMB,BMC.CMA sa rozwarte
b) katy AMB i BMC sa zawrte w przedziale <60;90> stopni

20 lip 16:34
 Zad.1/
Dany jest trójkąt równoramienny o podstawie długości "a" i ramionach długości "b"
oraz kącie między ramionami 20o
Wykaż,że spełniona jest równość : a3+b3=3ab2
zad.2/
Wykaż,że zachodzi równość: tg236o*tg272o=5
zad.3/
Jeżeli a,b>0 i a2+b2=10ab
Zad.1/
Dany jest trójkąt równoramienny o podstawie długości "a" i ramionach długości "b"
oraz kącie między ramionami 20o
Wykaż,że spełniona jest równość : a3+b3=3ab2
zad.2/
Wykaż,że zachodzi równość: tg236o*tg272o=5
zad.3/
Jeżeli a,b>0 i a2+b2=10ab




 Okręgi są oczywiście rozłączne.
Okręgi są oczywiście rozłączne.
 Ja tylko próbuje wskazać błą w treści a nie je rozwiązywać
Ja tylko próbuje wskazać błą w treści a nie je rozwiązywać 
 ?
?


 . Bo na przyklad prawa
strona moze byc ujemna. Nie wiadomo czy obie strony sa dodatnie
. Bo na przyklad prawa
strona moze byc ujemna. Nie wiadomo czy obie strony sa dodatnie



 . Wpaść na Twój pomysł to huhu
. Wpaść na Twój pomysł to huhu 



 aż do skutku
aż do skutku 
 ? Czy inna bajka ?
? Czy inna bajka ?
 zapisz sin10o=.... (z trójkąta
i sin30o =...
i już prawie ........
zapisz sin10o=.... (z trójkąta
i sin30o =...
i już prawie ........ 


 x=.........
x=.........
 Jak doprowadziłaś do dwóch nawiasów nie to że Cie
chcę sprawdzić ale czy tym najłatwiejszym sposobem to zrobiłaś.
Jak doprowadziłaś do dwóch nawiasów nie to że Cie
chcę sprawdzić ale czy tym najłatwiejszym sposobem to zrobiłaś.  Przepraszam za natręctwo.
Przepraszam za natręctwo. 






 Rozwiązuj zadania ....światek, piątek i niedziele
i tak "do końca świata i jeszcze jeden dzień dłużej"
Rozwiązuj zadania ....światek, piątek i niedziele
i tak "do końca świata i jeszcze jeden dzień dłużej" 

 . Teraz łatwe, tylko nie znałem wzoru sin3α, bo co prawda miałem trygonometrię w I
klasie, ale teraz w III klasie będę miał sin2α itd
. Teraz łatwe, tylko nie znałem wzoru sin3α, bo co prawda miałem trygonometrię w I
klasie, ale teraz w III klasie będę miał sin2α itd  . Zadanie 3 też jakoś z tych wzorów czy
nie?
. Zadanie 3 też jakoś z tych wzorów czy
nie? 

 narysuj trapez i ........
narysuj trapez i ........








 Hej Saizou
Hej Saizou  Taki rys. wystarczy?
Taki rys. wystarczy? 

 czy w moim rozwiązaniu zadania z trapezem jest gdzieś błąd
czy w moim rozwiązaniu zadania z trapezem jest gdzieś błąd


 <−−−− czy ja coś źle myślę
<−−−− czy ja coś źle myślę  ale to dżungla bez krokodyli i wszystkich innych stworzonek i niebezpiecznych roślin
ale to dżungla bez krokodyli i wszystkich innych stworzonek i niebezpiecznych roślin 

 ale musisz wykazać,że to dokładna wartość
a nie jak napisałeś ≈ 54o
ale musisz wykazać,że to dokładna wartość
a nie jak napisałeś ≈ 54o
 ( pomyłkowo wpisałam
( pomyłkowo wpisałam

 ( bo nie spojrzałam na oznaczenia na Twoim rys.
( bo nie spojrzałam na oznaczenia na Twoim rys.






 Miłych snów
Miłych snów 
 i również kolorowych
i również kolorowych

 (dżołk)
(dżołk)





 W trapezie o kątach ostrych 30o i 60o, zaś różnica kwadratów przekątnych trapezu wynosi 16
Oblicz pole tego trapezu.
W trapezie o kątach ostrych 30o i 60o, zaś różnica kwadratów przekątnych trapezu wynosi 16
Oblicz pole tego trapezu.
 Tak spójnia
Tak spójnia 





