Zadanie dla [z[bezendu]] 5-latek: Dane sa trzy punkty A(2.−1) B(1,3) i C(−1,1) bedace wierzcholkami trojkata . Znalezc katy tego trojkata

5-latek: bezendu to jest dla Ciebie to zadanie .

bezendu: ok

Piotr: Przepraszam, ze wchodzę w ten post ale mam pytanie .5−latek tutaj wychodzą ''ładne liczby'' czy nie?Mam na myśli, że mi cosα wyszedł w postaci ułamka nieskracalnego

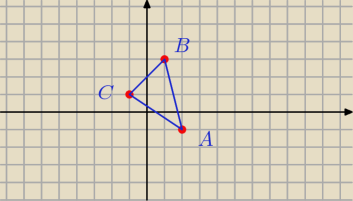
bezendu: A=(2,−1) B=(1,3) C=(−1,1) Czemu ja tu wyczuwam wektory wektor AC=[−1−2,1+1]=[−3,2] BC=−2,2 wektor AB=[1−2,3+1]=[−1,4] AC=−3,2 wektor BC=[−1−1,1−3]=[−2,2] AB=−1,4 długość wektora AC=√13 długość wektora AB=√17 długość wektora BC=2√2 kąt pomiędzy BC a AC

	10
cosα=		≈0,98≈120
	2√26

kąt między AC a AB

	11
cosα=		≈0,73
	√221

cosα≈43⁰ kąt między AB a BC

	10
cosα=		≈0,85
	2√34

cosα≈32⁰ ale coś nie tak bo suma kątów wyszła 87⁰

Piotr: Dlugość i wspolrzedne wektora mam tak samo. Pozniej ja zaczolem to robić tw. kosiniusów i

	3
wyszedl mi cosα=
	68

bezendu: 5−latek możesz podać prawidłowe odpowiedzi ?

5-latek: sprawdz jeszcze raz wektory bo zle ppoliczyles np BC[−2,−2]

5-latek: Piotr wyniki wychodza nieladne

bezendu: B=(1,3) C=(−1,1) (x₂−x₁,y₂−y₁) BC=[−1−1; 1−3]=[−2,−2]

5-latek: Bezendu w odpowiedzi mam takie wyniki

	11
cosA=
	√221

	3
cosB=
	√34

	1
cosC=
	√26

Piotr: Ok, dzieki za odpowiedzi. Tez mi takie wyszly

bezendu: @Piotr masz takie same długości i współrzędne wektorów jak ja ?

Piotr: Dlugość AB=√17 Dlugość AC=√13 Dlugosc BC=√8 Wspolrzedne AB=[−1,4] Wspolrzedne AC=[−3,2] Wspolrzedne BC=[−2,−2] Osobiscie robilem to z tw. kosiniusów

bezendu: ok dzięki, mi też już wyszły poprawne odpowiedzi

5-latek: Zadanie nr 2 Znalezc srodek i promin okregu opisanego na trojkacie o wierzcholkach A(−1,6)B(3,−2) i C(−4,−3)

5-latek: I na deser zadanie nr 3,. Z punktu S(6.4) jako z esrodka zatoczono okrag promieniem 10. Znale3zc punkty przeciecia tego okregu z dwusiecznymi katow ukladu wspolrzednych.

Piotr: Zadanie 2 Wyszlo mi (x−a)²+(y−b)²=r² S=(a,b) S=(−1,1) r=5 (x+1)²+(y−1)²=25 Zgadza się?

5-latek: Zgadza sie ale pokaz jak wyliczyles ten srodek

Piotr: Ok zaraz Ci napisze rozwiazanie

ZKS: Zadnie 3 wygląda na łatwe. Będą takie 4 punkty czy coś źle widzę?

Piotr: (x−a)²+(y−b)²=r² Dla punktu A układam równanie: 1. (−1−a)²+(6−b)²=r² Dla punktu B układam rownanie: 2. (3−a)²+(−2−b)²=r² Dla punktu C ukladam równanie: 3. (−4−a)²+(−3−b)²=r² Mam teraz uklad rownan z trzema niewiadomymi Przyrównuje 1 i 3 ze sobą i otrzymuję: a=2−3b Przyrównuję 2 i 3 ze soba i otrzymuję: 12+14a+2b=0 Wstawiam za a=2−sb i otrzymuję, że b=1 czyli a=−1 A promień mozna obliczyc w taki sposob, ze biore jedno rownanie i wstawiam a i b (−1+1)²+(6−1)²=r² r>0, zatem r=5

5-latek: Wy obydwaj robcie zadanie nr 3 (latwe ) a ja sie biore za rownania macierzowe .

5-latek: ZKS dobrze widzisz bo dopiero zobaczylem Twoj wpis

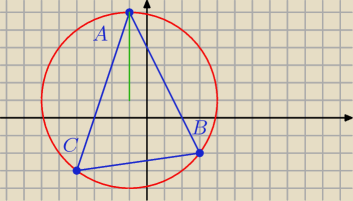
bezendu: A=(−1,6) B=(3,−2) C=(−4,−3) korzystam z równania okręgu (x−a)²+(y−b)²=r² (−1−a)²+(6−b)²=r² (3−a)²+(−2−b)²=r² (−4−a)²+(−3−b)²=r² 1+2a+a²+36−12b+b²=r² 9−6a+a²+4+4b+b²=r² 16+8a+a²+9+6b+b²=r² a²+2a+b²−12b+37−r²=0 a²−6a+b²+4b+13−r²=0 a²+8a+b²+6b+25−r²=0 a²+2a+b²−12b+37−r²=a²−6a+b²+4b+13−r² 8a−16b+24=0/8 a−2b+3=0 a²−6a+b²+4b+13−r²=a²+8a+b²+6b+25−r² −14a−2b−12=0 /2 −7a−b−6=0 a−2b=−3 7a+b=−6 /2 a−2b=−3 14a+2b=−12 15a=−15 a=−1 −1−2b=−3 −2b=2 2b=2 b=1 wstawiam do pierwszego równania 1+2a+a²+36−12b+b²=r² 1−2+1+36−12+1=r² r²=25 r=25 S=(−1,1) r=5

bezendu: @Piotr w temacie było zadania dla bezendu ale 3 możesz zrobić

Piotr: Wiem, przepraszam . Tak sobie robilem i chcialem sprawdzic czy dobrze. I @5−latek chcial, zebym napisal rozwiazanie to napisalem

bezendu: to nie wiem po co ja produkowałem swoje rozwiązanie

5-latek: bezendu Sroek mogles znalezc tez w ten sposob ze napiszesz rownania symetralnych dwoch bokow i znadziesz punkt ich przeciecia

Piotr: Przepraszam jeszcze raz . Spojrz na moje rozwiazanie, w skrocie je napisalem tylko . Już nie bede pisal

bezendu: mam drobny błąd w układzie równań −1−2b=−3 −2b=−2 2b=2 b=1

5-latek: No to zrob tym sposobem i zobacz czy wyjdzie tak samo tylko wektorami

ZKS: To ja dam dla was zadanie żeby później nie było że ktoś zrobił jego zadanie. Rozwiąż równanie: tg²(x + y) + ctg²(x + y) = 1 − 2x − x².

bezendu: 5−latek nawet chyba szybciej by to wyszło, ale skoro przyrównywałem te równania to wyznaczenie środka zrobiłem układem równań (Skąd masz to zadanie ? )

bezendu: @Piotr nie robić pierwszy zamówiłem ZKS za 10 minut podam Ci wynik bo nie mam czasu na rozpisanie rozpiszę jutro mam nadzieję że sięnie obrazisz ?

Piotr: Spoko, już pisalem ze nie bede robil

ZKS: To za chwilę dla Ciebie Piotr podam inne zadanie jeżeli chcesz?

5-latek: Ale zrob to wektorami tutaj −to jest przeciez gfeometria analityczna

Piotr: Okej, możesz dać

bezendu: @ZKS x=1 y=−2 ? 5−latek dziś już tego nie zrobię wektorowa, ale obiecuję że jutro po 10 rozwiąże to i zrobię zadanie 3 A tymczasem miłego wieczoru dla Wszystkich i

ZKS: Nie. W odpowiedzi są podane inne rozwiązania.

5-latek: Dalej geometria analityczna dla Piotrka . I jeszcze dostaniesz od ZKS to bedziesz miaql co robic Zadanie . Dane sa wierzcholki trojkata A(−1,−1) B(1,−3) i C(−4,1) Znalezc punkt przeciecia dwusiecznej kata zewnetrznego przy wierzcholku A z przedluzeniem boku BC

Piotr:

ZKS: Piotr pozwalam Ci wybrać dział z którego chcesz zadanie.

Piotr: Wielomiany mogą być

ZKS: Okej za chwilę coś napiszę.

Eta: A ja mogę ?

ZKS: Wykaż że nierówność x⁴ + 2x³ + 3x² + 2x + 2 > 0 jest spełniona przez każdą liczbę rzeczywistą x.

Piotr: Zadanie @ 5−latek narazie nie mam pomyslu jak ruszyc. Wiec sprobuje z wielomianem

ZKS: Eta chcesz dawać zadania czy rozwiązywać?

krystek: Oj , Eta dopiero wystartowała do LO , więc może nie da rady. Pozdrawiam Eto

Eta: Witaj krystek @ZKS ....... oczywiście,że zadawać! (już się narozwiazywałam

Piotr: Wykaż że nierówność x⁴ + 2x³ + 3x² + 2x + 2 > 0 jest spełniona przez każdą liczbę rzeczywistą x x⁴+2x³+2x²+x²+2x+2>0 x²(x²+1)+2x(x²+1)+2(x²+1)>0 [x²+1][x²+2x+2]>0 x⁺2x+2=0 Δ=4−8<0, zatem brak miejsc zerowych, wspolczynnik a>0 wiec ramiona paraboli sa skierowane do gory a więc x²+2x+2>0 x²+1>0 A zatem: [x²+1][x²+2x+2]>0 c.n.u.

5-latek: Dobry wieczor Krystek. Milo Cie powitac na forum

Eta: Pięknie .......

krystek:

ZKS: A masz pomysł na inny sposób wykazania że jest to spełnione?

Eta: No to zadanie ode mnie 1/ Wielomian W(x)= x⁴+6x³+5x²+12x−9 przedstaw w postaci iloczynu dwu wielomianów st. 2 o współczynnikach całkowitych i o współczynnikach 1.. przy drugich potęgach x

Piotr: Zaraz pomysle . @Eta Twoje tez niedlugo zrobie. Tylko Tacie dam na 15 minut wejsc na kompa

Eta: Ok

ZKS: Następne daje jak coś. Rozwiąż nierówność (x − 4)√x + 1 < 4 − 2x.

Piotr: Inny pomysl na zadanie @ZKS'a: x⁴+2x³+2x²+x²+2x+2>0 (x²+x)²+2(x²+x+1)>0 (x2⁺x)²>0 dla x∊R x²+x+1>0 dla x∊R, gdyż Δ<0 oraz wspolczynnik a>0 a zatem (x²+x)²+2(x²+x+1)>0 dla kazdego x∊R c.n.u.

ZKS: To jeszcze inny sposób x⁴ + 2x³ + 3x² + 2x + 2 > 0 x⁴ + 2x³ + x² + x² + 2x + 1 + x² + 1 > 0 (x² + x)² + (x + 1)² + x² + 1 > 0 (x² + x) ≥ 0 dla każdego x ∊ R (x + 1)² ≥ 0 dla każdego x ∊ R x² + 1 > 0 dla każdego x ∊ R zatem całe wyrażenie x⁴ + 2x³ + 3x² + 2x + 2 jest > 0.

5-latek: Np tez takie zadanie ze zbioru Antonowa

	x1/2+1		1
Uproscic wyrazenie		:
	x+x1/2+1		x1,5−1

5-latek: Mialo byc na koncu

Saizou : mogę się dołączyć

Piotr: Pewnie, że tak

Piotr: Eta zrobilem Twoje Zadanie wyszlo mi: (x²+x+3)(x²+5x−3) lub (x²+x−3)(x⁺5x+3) Dobrze czy zle ?

ZKS: Rozłóż na czynniki możliwie najniższego stopnia wyrażenie x⁴ + x³ + x² + x + 1.

Piotr: Poprawienie ''..... lub (x²+x−3)(x²+5x+3)

ZKS: Jak dostałeś dwa wyrażenia Piotr? To drugie jest nie zgadza się z wielomianem wyjściowym. Pokaż jak to robisz.

Piotr: Chwilka chyba wiem juz czemu. Napisze rozwiazanie niedlugo tego zadania

Saizou : zadanie od Ety ten wielomian ma być przedstawiony w postaci (x²+ax+b)(x²+cx+d), ale wiemy że wyraz wolny =−9, zatem iloczyn bd=−9, wówczas mamy możliwości b=1 i d=−9 albo b=3 i d=−3 (pomijam inne kombinacje bez start dla zadania) i współczynniki mają być całkowite (x²+ax+1)(x²+cx−9) albo (x²+ax+3)(x²+cx−3) i teraz wystarczy to rozwiązać porównać wielomiany i sprawdzić czy rozwiązania są liczbami całkowitymi

Piotr: Rozwiązanie 1/ Wielomian W(x)= x⁴+6x³+5x⁺12x−9 przedstaw w postaci iloczynu dwu wielomianów st. 2 o współczynnikach całkowitych i o współczynnikach 1.. przy drugich potęgach x. W(x)=(x²+bx+c)(x⁺dx+e)=x⁴+6x³+5x²+12x−9 W(x)=x⁴+dx³+ex²+bx³+bdx²+bex+cx²+cdx+ce=x⁴+x³(b+d)+x²(e+bd+c)+x(be+cd)+ce Przyrównuje teraz wspolczyniki tego wielomianu: b+d=6 e+bd+c=5 be+cd=12 ce=9 ce=9 . Wspolczyniki maja byc liczbami calkowitymi a więc 1. c=1 i e=−9 V 2.c=3 I e=−3 Rozpatruje pierwszy przypadek 1.−9b+d=12 −9(6−d)+d=12 d=6,6∉ C A więc ten przypadek odpada Rozpatruje drugi przypadek 2. −3b+3d=12 −3(6−d)+3d=12 d=5∊C b=6−5=1∊C A zatem: c=3 , e=−3 , d=5 , b=1 W(x)=(x⁺x+3)(x²+5x−3)

Piotr: Sorry Saizou, ale nie wiedzialem ze wczesniej pisales

Saizou : nie, ok, ja kiedyś też dostałem to zadanie do Ety

Saizou : zresztą i tak nie napisałem odpowiedzi

Piotr:

ZKS: A nie lepiej jest zrobić tak x⁴ + 6x³ + 5x² + 12x − 9 = x⁴ + 6x³ + 9x² − 4x² + 12x − 9 = (x² + 3x)² − (2x − 3x)² = (x² + 3x − 2x + 3)(x² + 3x + 2x − 3) = (x² + x + 3)(x² + 5x − 3). Ale jak kto woli zresztą.

Saizou : ZKS też tak myślałem tylko mi zabrakło wzorku a²−b² szkoda gadać

ZKS: To następne zadania już na was czekają.

Eta:

bezendu: 5−latek zrobiłem to wektorowa, tak jak kazałeś i wyszło to samo. Na zadanie 3 brak pomysłu

Trivial: bezendu: chodzi o zadanie "Z punktu S(6.4) jako z esrodka zatoczono okrag promieniem 10. Znale3zc punkty przeciecia tego okregu z dwusiecznymi katow ukladu wspolrzednych."?

5-latek: Witaj. jesli chodzi o zadanie nr 3 to naprawde pomoze prawidlowo wykonany rysunek Jakie bedzie rownanie dwusiecznej katow ukladu wspolrzednych przechodzacej prztz 1 i 3 cwiartke . To samo przechodzacej przez 2 i 4 cwiaeke ? Jak bedzie to wiedzial juz pryszcz

5-latek: jak to zrobisz to sprobuj zrobic zadanie z godz 21.35 i 22.56. to z 22,56 tez jest ciekawe

bezendu: ok

5-latek: No to troche CI podpowiem Rownanie dwusiecznej katow przechodzacej przez 1 i 3 cwiartke ukladu wspolrzednych ma postac y=x

bezendu: a druga i czwartą y=−x ?

5-latek: tak

bezendu: (x−6)²+(y−4)²−10=−x (x−6)²+(y−4)−10=x

ZKS: Ale co teraz zrobiłeś?

bezendu: równania okręgu przyrównane z równaniem dwusiecznych kątów aby wyznaczyć punkty przecięcia

ZKS: Niestety to źle robisz. Skoro masz proste y = ±x oraz równanie okręgu (x − 6)² + (y − 4)² = 100 to nic nie przyrównujesz tylko wstawiasz w miejsce y = ±x i rozwiązujesz równanie kwadratowe tylko tyle.

bezendu: x²−12x+36+x²−8x+16=100 2x²−20x+52=100 2x²−20x−48=0 x²−10x−24=0 Δ=10²−4*(−24) Δ=196 √Δ=14

	10−14
x1=		=−2
	2

	10+14
x2=		=12
	2

x=−2 x=12 y=−2 y=12 (x−6)²+(−x−4)²=100 x²−12x+36+x²+8x+16=100 2x²−4x+52=0 2x²−4x−48=0 x²−2x−24=0 Δ=100 √Δ=10

	2−10
x1=		=−4
	2

	2+10
x2=		=6
	2

x=−4 x=6 y=4 y=−6

ZKS: Git. Rób następne.

bezendu: To równanie zrobiłem jeszcze raz dziś rano wyniki x=−1 y=2 ? teraz się zgadza ?

ZKS: Wstaw i sprawdź.

bezendu: teraz właśnie się zgadza L=P ale czy w książce też się zgadza ?

ZKS: Hmm jak to się zgadza mi wychodzi sprzeczność. tg²(x + y) + ctg²(x + y) = 1 − 2x − x² tg²(−1 + 2) + ctg²(−1 + 2) = 1 − 2 * (−1) − (−1)² tg²(1) + ctg²(1) = 2 [tg(1) − ctg(1)]² = 0 ⇒ sprzeczność ponieważ tg(1) > 0 oraz 0 < ctg(1) < tg(1).

bezendu: https://matematykaszkolna.pl/forum/7226.html zobacz tam wyszły takie same wyniki jak u mnie x=−1 y=2

ZKS: Ale zobacz przecież że udowodniłem Tobie że to nie jest prawdą.

ZKS: Znalazłeś rozwiązanie ale niestety nie jest poprawne gdybyś się pofatygował sprawdzić poprawność rozwiązania sam byś zauważył.

bezendu: zrobię jeszcze raz to zadanie

ZKS: To zrób ale samemu wtedy się czegoś nauczysz ponieważ będziesz kombinował jak je zrobić.

bezendu: zrobiłem samemu ale najpierw wyszło x=1 y=−2 post 21:32 i napisałeś, że to jest źle więc zamieniłem liczby znaki w rozwiązaniu x=−1 y=2 i nadal źle ?

ZKS: Podstaw i sprawdź.

ZKS: Najlepiej będzie jak będziesz pisał jak robisz to będzie można wskazać błąd albo naprowadzić na poprawne rozwiązanie.

bezendu: x jest na pewno −1 , możesz napisać rowiązanie dla y?

ZKS: A skąd na pewno wiesz że x = −1? Nie mówię że źle tylko dlaczego?

ZKS: Pisać rozwiązanie całe?

bezendu: tak

ZKS: Już piszę.

ZKS: tg²(x + y) + ctg²(x + y) = 1 − 2x − x² Zauważamy że zbiór wartości funkcji f(x ; y) = tg²(x + y) + ctg²(x + y) wynosi ZW = [2 ; ∞)

	1
ctg2(x + y) =		a wiemy że średnia arytmetyczna jest ≥ od
	tg2(x + y)

	a + b
średniej geometrycznej		= √ab zatem niech tg2(x + y) = z tak więc
	2

1   z +   z		1
	≥ (z *		)1/2
2		z

	1
z +		≥ 2
	z

g(x ; y) = 1 − 2x − x² wynosi ZW = (−∞ ; 2] tak więc jedyny punkt wspólny istnieje dla x = −1 ponieważ

	2
wartość maksymalna funkcji g(x ; y) równa 2 jest dla xw =		= −1 zatem wstawiamy w
	−2

miejsce x = −1 i patrzymy co dostajemy tg²(−1 + y) + ctg²(−1 + y) = 2 tg²(−1 + y) + ctg²(−1 + y) − 2 = 0 wiemy że tg(α) * ctg(α) = 1 więc tg²(−1 + y) − 2 * tg(−1 + y) * ctg(−1 + y) + ctg²(−1 + y) = 0 wzór a² − 2ab + b² = (a − b)² [tg(−1 + y) − ctg(−1 + y)]² = 0 tg(−1 + y) = ctg(−1 + y)

	π
tg(−1 + y) = tg(		+ 1 − y)
	2

	π
−1 + y =		+ 1 − y + k * π
	2

	π
2y =		+ 2 + k * π
	2

	π		π
y =		+ 1 + k *		.
	4		2

Mam nadzieję że wszystko jest zrozumiałe jeżeli nie to pisz postaram się wyjaśnić.

bezendu: do x=−1 wszystko jest jasne bo tyle zrobiłem, ale potem jak zwijasz do wzoru skróconego mnożenia to czemu tg(−1+y)=ctg(1+y) ?

ZKS: Skoro (a − b)² = 0 to |a − b| = 0 a − b = 0 ⇒ a = b. Kwadrat dowolnej liczby rzeczywistej jest równy 0 tylko wtedy kiedy ta liczba jest zerem.

ZKS: Ale należało wykazać że x = −1 jest rozwiązaniem Ty tego nie wykazałeś tylko przyjąłeś od tak.

bezendu: dalej już wszystko jasne dzięki

ZKS: Mogę powiedzieć że to zadanie na pewno do tych łatwych nie należało. Nie ma za co. Następne zadania czekają.

bezendu: jeszcze aksjomat czeka a ten wielomian na pewno jest dobrze przepisany ?

ZKS: Który wielomian?

bezendu: post 23:07 ?

ZKS: On nie jest przepisany sam go wymyśliłem ale jest na 100% dobrze zapisany.

5-latek: bezendu a tamtych nie probujesz rozwiazac?

bezendu: próbuje, ale najpierw muszę zrobić zadania z aksjomatu

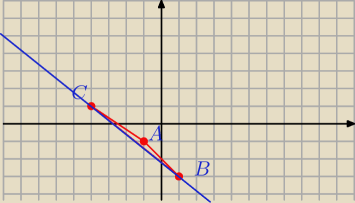
bezendu: Zadanie . Dane sa wierzcholki trojkata A(−1,−1) B(1,−3) i C(−4,1) Znalezc punkt przeciecia dwusiecznej kata zewnetrznego przy wierzcholku A z przedluzeniem boku BC prosta BC

	4		11
−		x−
	5		5

dalej na razie nie mam pomysłu

5-latek: Te punkty leza bardzo bardzo blisko siebie wiiec moze narysuj to w wiekszej skali bedziesz lepiej widzial Teraz ktore proste wyznaczaja ten kat zewnetrzny przy wierzcholku A ? Sa 2 takie katy zewnetrzne przy wierzcholku A Teraz z geomertrii co nazywamy katem zewwnetrznym trojkata ? Co to jest dwusieczna kata . Jesli mamy dwie proste ktore tworza kat to jakim zbiorem punktow jest dwusiecza od tych prostych? jesli jest zborem punktow r.......o oddalonych od tych prostych to jak mozemy zaopisac rownanie dwusiecznej ? na razie tyle podpowiedzi

bezendu: ok za 15 sprubuje

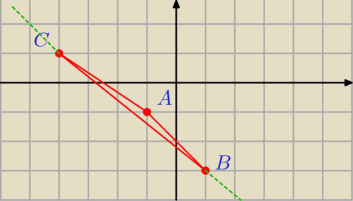
bezendu: prosta przechodząca przez punkty b i c

	4		11
y=−		−
	5		5

dwusieczna będzie raczej przechodzić przez środek odcinka CB a nie przez przedłużenie prostej BC

5-latek: Moze nie przez srodek ale tak by bylo gdy to byl kat wewnwetrzny a tutaj potrzebny jest kat zewnwtrzny przy wierzcholku A Nastepna podpowiedz . Katem zewnetznym trojkata nazywamy kat przylegly do kata wewnwntrznego

5-latek: A tak nawiasem mowiac to przez srodek boku przechodzi srodkowa(symetralna) i dwusieczna kata wewnetrznego przy wierzcholku w trokkacie rownoramiennym

bezendu: nie wiem jak to zrobić zrobiłem to z ciągiem które dałeś w innym wątku

5-latek: Moze Mila lub Eta pomoze z rysunkiem ale zobacz jeli zrobisz przedluzenie prostej CA to wlasnie kat BAC' bedzie katem zewnetrznym przy wierzcholku A i to samo jesli zrobisz przedluzenie prostej AB to kat CAB' bedzie tez katem zewnetrzym przy wierzcholku A Suma katow przyleglych =180 stopni wiec kat z ewnetrzny ma miare 180 stopni − kat wewnetrzny do niego przylegly. Teraz moze juz jasniej bedzie troche

Mila: Rysunek z 21:31 jest dobry.

5-latek: dzien dobry Milu . Tylko chodzi o to zeby mu pokazac na rusunku jak ta dwusieczna kata zewnetrznego przy wierzcholku A bedzie przebiegac

Mila: Teraz muszę przerwać, później narysuję. Witam i pozdrawiam.

5-latek: Tez wlasnie musze isc do rodzicow zobaczyc co u nich slychac . Ale zadanko jest ciekawe?

pigor: co do zadania z dwusieczną kąta zewnętrznego, czy na pewno współrzędne wierzchołków Δ są takie właśnie, bo jeśli tak to jakiś sadysta je sobie wymyślił, każąc się męczyć z układem równań : dwusiecznej : (2√2+√13)x+(3√2+√13)y+5√2+2=0 (druga dwusieczna nie przetnie przedłużenia boku BC) i prostej zawierającej BC o równaniu : 4x+5y+11=0, ale cóż jak ktoś lubi lub nie ma co robić, niech się pobawi tym układem ...

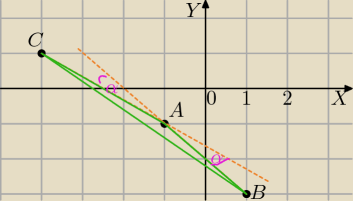
Mila: Dane sa wierzchołki trojkata A(−1,−1) B(1,−3) i C(−4,1) α− kąt zewnętrzny kąta A AB: y=−x−2 AC:

	−2		5
y=		x−
	3		3

BC:

	−4		11
y=		x−
	5		5

P(x,y) punkt należący do dwusiecznej kata α jest jednakowo odległy od prostych AC i AB równanie dwusiecznej wynik brzydki. II sposób Z tw. o dwusiecznej kata zewnętrznego E punkt przecięcia dwusiecznej z bokiem BC CE:BE=AC:AB (√41+x):x=√13:√2

5-latek: Przepisalem to zadanie ze zbioru zadan. zaraz znajde odpowiedz i podam A wiec tak wynik to (−11,−3)

bezendu: Można znać tytuł tego zbioru ?

Mila: To mi się nie zgadza, może inne wsp. wierzchołków. Punkt (−11,−3) nie leży na prostej BC

5-latek: B. Gdowski E Plucinski . Zadania z rachunku wektorowego i geometrii analitycznej Na allegro znajdziesz

bezendu: Dziękuje

5-latek: Mila sprawdzalem 5 razy te wsolrzedne czy dobrze przepisalem zanim napisalem zadanie . Byc moze jest blad . Nie rozwiazywalem tego Patrzylem tez teraz na errate i nie ma z e jest blad .

5-latek: Milu jesli posiadasz tez zbior to jest to zadanie nr 243 .

5-latek: Teraz patrzac na ten rysunek masz racje bo ten punkt nie nalezy do prostej BC

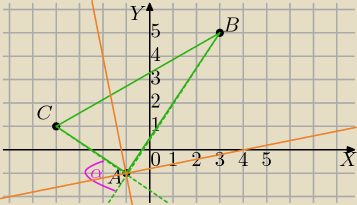
Mila: A=(−1,−1), B=(3,5), C=(−4,1) AC:

	−2		5
y=		x−		/ *3⇔3y=−2x−5⇔2x+3y+5=0
	3		3

BC:

	4
y=		x+(23/7) /*7
	7

7y=4x+23⇔4x−7y+23=0 AB:

	3		1
y=		x+		/*2
	2		2

2y=3x+1⇔3x−2y+1=0 α− kat zewnętrzny P(x,y) punkt należący do dwusiecznej kata α jest jednakowo odległy od prostych AC i AB Dwusieczna:

|2x+3y+5|		|3x−2y+1|
	=
√22+32		√32+22

2x+3y+5=3x−2y+1 lub 2x+3y+5=−3x+2y−1 5y=x−4 lub y=−5x−6

	1		4
y=		x−		lub y=−5x−6 są dwie dwusieczne między prostymi AC i AB
	5		5

	1		4
d: y=		x−		dwusieczna kąta zewnętrznego
	5		5

Punkt przecięcia: 5y=x−4 i 4x−7y+23=0 x=−11 i y=−3

5-latek: Milu to u mnie w zadaniu byl blad jednak Wspolrzedne punktu B byly inne

bezendu: 5−latekpost pigora 19:10

Mila: Tak w Twoim zbiorze jest błąd, co więcej , zadanie to widziałam w zestawach zadań dla uczniów w Twojej wersji. Pigor ma rację, sadysta wymyślił te współrzędne.

Mila: Zadanie jest ciekawe i Bezendu spróbuj go rozwiązać.

bezendu: dobrze Mila rozwiąże jutro po 17 wcześniej nie dam rady

pigor: ...tak, w moim Gdowskim jest zad, 243 i punkt B=(3,5) , sądzę, że jakiś belfer(ka) zmienił(a) sobie bezmyślnie te współrzędne i był(a) zapewne z tego powodu ... bardzo dumny(a) , lecz zarazem durny(a) ; przepraszam, ale takie rzeczy mnie − delikatnie mówiąc − wkurzają . ...

5-latek: Chodzi o to ze jest to zadanie z Gdowskiego −zbior z 1967r −tam w zadaniu jest blad

5-latek: Bezendu dlaczego nie probujesz ? Pigor tylko z drugiej strony nie jest zasada ze wyniki musza wyjsc zawsze ladne . Niech tylko dellta wyjdzie np 30 to juz pisza ze cos zle bo nie idzie ladnego wyciagnac pierwiastka z delty i takze jak trzeba cos policzyc z pierwiastkiem to wolaja ratunku

5-latek: Ja juz to rozwiazesz to masz nastepne Znalezc srodek okregu wpisanego w trojakt o wierzcholkach A(75,75) b(175,0) C(147.−21) .Oczywiscie uklad wpsolrzednych prostokatny . Przydadza sie wiadomosci z tego zadania o kacie zewnetrzym

bezendu: Punkty A=(−1,−1) B=(1,−3) C=(−4,1) prosta AB −x−y−2=0 x+y+2=0 prosta AC

	2		5
y=−		x−		/3
	3		3

3y=−2x−5 2x+3y+5=0 prosta AB

	4		11
y=−		+		/5
	5		5

5y=−4x+11 4x+5y−11=0

	|2x+3y+5|
U{|x+y+2|}{√12+12=
	√22+32

x+y+2=2x+3y+5 ∨ x+y+2=−2x−3y−5 −x−2y−3=0 3x+4y+7=0 −2y=x+3 2y=−x−3

	1		3
y=−		x−
	2		2

	1		3		4		11
−		x−		=−		x+
	2		2		5		5

	3		37
		x=
	10		10

	37
x=
	3

	23
y=−
	3

5-latek: To sprawdz teraz czy ten punkt nalezy do prostej BC . jesli tak to jest OK. Ale tez juz wiesz ze punkt B jest inny . Teraz zrob to zadanie z okregiem wpisanym . Wiesz gdzie lezy srodek okregu wpisanego w trojakt

bezendu: 5−latek dziś chciałem porobić zadanie tego typu https://matematykaszkolna.pl/forum/208260.html

ZKS: To rób chętnie zobaczę te zadania.

5-latek: NO to masz.

	1		1		1
Wykaz z ejezeli a,b i c sa liczbami dodatnimi to (a+b+c)(		+		+		)≥9
	a		b		c

ZKS: Dziękować zaraz zrobię.

ZKS: Udowodnij że suma sześcianów trzech kolejnych liczb naturalnych jest podzielna przez 9.

ZKS: Nie tutaj miało być wrzucone zadanie.

ZKS: Wrzucać mam rozwiązanie 5−latek czy to dla bezendu?

5-latek: ZKS to jest dla bezendu bo prosil . ja dzisiaj nie rozwiazuje bo jestem zmeczony po pracy

bezendu: trzy kolejne liczby naturalne n∊C (n−1)²n³+(n+1)³= n³−3n²+3n−1+n²+n³+3n²+3n+1= 3n²+6n=3n(n+2) wyrażenie to jest wielokrotnością liczby 3 więc dzieli się przez 3 a co za tym idzie również przez 9 ?

ZKS: To wrzucone było dla bezendu jak coś ode mnie. To miłego odpoczynku życzę.

ZKS: A czy 3 dzieli się przez 9?

ZKS: Masz kolejne ale dokończ te poprzednie jak coś. Wykaż że 777⁵ + 444⁴ − 333²¹ jest liczbą podzielną przez 10.

bezendu: ale 9 dziel się przez 3

ZKS: No tak 9 dzieli się przez 3 ale 3 przez 9 już nie więc nie udowodniłeś jeszcze tego.

bezendu: pamiętasz tą 6n to dzieliło się przez 6 więc 3n jest podzielne przez 9 ? wgl dowód jest ok czy komentarz nie poprawny ?

5-latek: ZKS jeszcze jedno dalem tutaj na koncu https://matematykaszkolna.pl/forum/208260.html

ZKS: To nie jest jeszcze dowód przedstawiłeś tylko wyrażenie (n − 1)³ + n³ + (n + 1)³ w innej postaci. Komentarz poprawny i dowód jest w całości dobry ale ten komentarz szwankuje.

ZKS: Okej będę patrzył 5−latek czy bezendu je robi.

ZKS: Tak poza tym bezendu to coś zgubiłeś na końcu powinieneś otrzymać 3n³ + 6n.

bezendu: to nie rozumiem co jest źle w tym dowodzie ?

bezendu: 3n³+6n=3n(n²+6)

ZKS: Napisałeś że wielokrotność liczby 3 jest podzielna przez 9 a to przecież nie jest prawda. Czy 3 * 1 ; 3 * 2 ; 3 * 4 i tak dalej są podzielne przez 9?

ZKS: No i teraz kombinuj.

bezendu: ale potem sprostowałem, a Ty się teraz czepiasz

5-latek: Dziekuje

ZKS: Ale co sprostowałeś?

bezendu: 3n(n²+2) 3n[(n²−1)+3] 3n(n−1)(n+1)+3 (n−1)(n+1)3n+9n

bezendu: ZKS post 21:57

Eta: Teraz piknie .......

bezendu: piknie ?

Eta: Napisz jeszcze komentarz

bezendu: 3(n−1)n(n+1)+9n są to trzy kolejne liczby całkowite więc co najmniej jedna z nich musi być podzielna przez 3 więc wyrażenie jest podzielne przez 3 ?

ZKS: Masz udowodnić że przez 9 nie 3.

bezendu: a no tak są.........podzielne przez 9 ? ok teraz ?

ZKS: Ale dlaczego napisałeś że jest to podzielne przez 9 ale nie napisałeś dlaczego.

5-latek: Bezendu zebys nie zapomnial to zostalo jeszcze zadanie z godz 19.51

asdf: Nie czytalem odpowiedzi (wiem, leń ze mnie), jezeli byla udzielona, to mozna zingnorować: "Dane sa trzy punkty A(2.−1) B(1,3) i C(−1,1) bedace wierzcholkami trojkata . Znalezc katy tego trojkata" wskazówka: zrobic wektory AB^→=a^→, BC^→=b^→, AC^→=c^→, stosując wzór:

	a→◯b→
cos(a→,b→) =
	|a→|*|b→|