k Sinusoidalny ruch prostego osc: nie ma co robić dajcie zadanko na pozioie 1 lo

Godzio: Znaleźć taką najmniejszą liczbę naturalną n, aby liczby postaci n + 1 oraz n − 110 były kwadratami liczb naturalnych

Sinusoidalny ruch prostego osc: n+1 = x² ∧ n−110 = y² x² − y² = (n+1) − (n−110) = 111 x² − y² = (x−y) (x+y) = 111 111 = 3 * 37 << liczby naturalne pierwsza: x +Y = 37 x − y = 3 2x = 40 x − 20 n= 20² − 1 n = 399 druga: x+y = 1 x − y = 111 2x = 112 x = 56 n = 56² − 110 n= 3135

Godzio:

Sinusoidalny ruch prostego osc: czyli mam isc spac ? nie ma wiecej?

Godzio: Udowodnij, że punkt styczności okręgu wpisanego w trójkąt prostokątny z przeciwprostokątną dzieli tę przeciwprostokątną na odcinki, których iloczyn jest równy polu tego trójkąta.

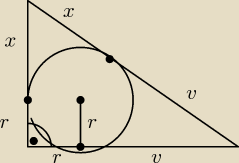
Sinusoidalny ruch prostego osc: ale to nie prawda . Punkt styczności dzieli przeciwprostokątną ale na przyprostokątne zmniejszone o r

Sinusoidalny ruch prostego osc: Dobrze myślę ?

Sinusoidalny ruch prostego osc: jest ktos bo nie iwem czy czekac?

Sinusoidalny ruch prostego osc: halo

asdf: pitagorasem

Sinusoidalny ruch prostego osc: Nie rozumie

Godzio: Kombinuj To jest prawda, pamiętaj, że pole prostokąta to iloczyn przyprostokątnych podzielony przez 2.

Sinusoidalny ruch prostego osc: No wiem ale jestem w łóżku i nie mam jak. Jeśli możesz dodaj jeszcze jedno zadanie to zrobię je oba jutro

Sinusoidalny ruch prostego osc:

5-latek: https://matematykaszkolna.pl/forum/208071.html Nie zrobiles tych 2 zadan ktore napialem 1.07 godz 23.36

Godzio: No i masz kolejne Ja idę spać, bo rano trzeba wstać, dobranoc

Sinusoidalny ruch prostego osc: Ok juz wiem ze : r² + rv + xr to pole trójkąta Ale nie umiem tego przekształcić do x * r

Sinusoidalny ruch prostego osc: 5−latek twoich zadań nie wiem jak zrobic

5-latek: https://matematykaszkolna.pl/forum/208074.html W tym poscie dostales podpowiedz jak rozlozyc mianownik tego wyrazenia . Z licznikiem tez pokombinuj tak samo

5-latek: To zadanie nr 1 jest z egzamimu na studia ekonomoczne dla pracujacych z 1971r .

Sinusoidalny ruch prostego osc: W praktyce osoba zajmująca sie ekonomia korzysta z takich obliczeń?

5-latek: W praktyce pewnie nie . Ale to mial byc przyszly student wiec musial umiec takie obliczenia wykonywac

5-latek: Ale zrobiles to dalej . jesli tak to pokaz rozwiazanie

Godzio: I jak ?

sunus: @Godzio nie wiem

Sinusoidalny ruch prostego osc: s

Sinusoida: Jak to zrobić?

Godzio:

	a + b − c
Wykorzystaj to, że r =		(łatwo wyprowadzić − a najlepiej to wyprowadź)
	2

Dalej zadanie jest banalne

Sinusoidalny ruch prostego osc: r² + rv + xr = xr (a+b−c)² + a+b−c * 2v + a+b−c * x = a+b−c * x/ − a+b−c * x (a+b)−c)² + a+b−c * 2v = 0 a² + 2ab + b² − 2ac +2ab +c² +a+b−c * 2v = 0 a² + b² + c² +2ab +2ac +2ab +a+b−c * 2v = 0 a² + b² + c² +2(2ab+ac+av+bv−cv) = 0

Sinusoida: To jak ?

Sinusoidalny ruch_prostego os: Jak to zrobić ?

pigor: ..., to ja pokażę, ale ty musisz nieco uważniej przyjrzeć się swojemu rysunkowi powyżej i odpowiedzieć sobie dlaczego , a więc np. tak : z poczciwego tw. Pitagorasa masz (r+v)²+(r+x)²= ((x+v)² ⇔ r²+2rv+v² + r²+2rx+x²= x²+2xv+v² ⇔ ⇔ 2rv+2r²+2rx= 2xv /:2 ⇔ rv+r²+xr= xv ⇔ r²+(x+v)r = xv= S c.n.u. .

Sinusoida: Aaaaas