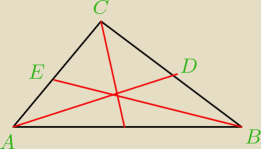
Planimetria bezendu: Udowodni, że trzy środkowe rozcinają trójkąt na sześć części o równych polach jak to udowodnić ?

Mila:

	1
1) PΔ=		a*h ( zauważ które Δ mają tę samą wysokość)
	2

2) środkowa dzieli bok na połowy

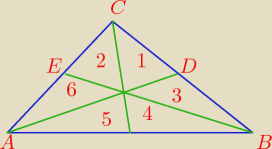
bezendu: trójkąt 5 i 4 trójkąt 1 i 2 trójkąt 3 i 6 zgadza się ?

Mila: Δ5 i Δ4 Δ1 i Δ3 Δ2 i Δ6 P_{Δ5 +Δ6+Δ2}=P_Δ4+Δ3+Δ1 Możesz też wykorzystać to,że : punkt przecięcia środkowych dzieli każdą z nich w stosunku 2:1 (licząc od wierzchołka).

bezendu: Czyli jak napiszę to co Ty mi napisałaś P_Δ5+Δ6+Δ2=P_Δ4+Δ3+Δ1 to będzie kończyło dowód ?

Mila: To Ci pomoże. Masz pokazać, że : P₁=P₂=P₃=P₄=P₅=P₆

Eta: https://matematykaszkolna.pl/forum/18847.html

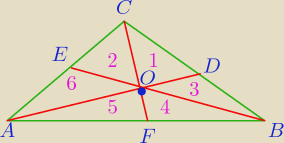
bezendu: Ta wysokość dzieli się w stosunku 2:1 ?

Eta: każda środkowa dzieli trójkąt na dwa trójkąty o równych polach !

bezendu: ok dziękuję

Eta: drugi sposób zatem : P₅= P₄ i P₆=P₂ i P₃= P₁ i P₂+P₆+P₅= P₁+P3+P₄ kombinuj dalej

Eta: tzn. inny sposób od tego ,który podał Bogdan

Mila: Nie piszę rozwiązania, bo wiem, że sam to rozwiążesz, korzystając z podanych własności.

bezendu: P_Δ45+P₂₆=P_Δ45+P_Δ13 ?

Eta: https://matematykaszkolna.pl/forum/204276.html

bezendu: Dziękuje ale planimetria nie jest moją mocną stroną niestety

Mila: Teraz przećwicz te sposoby, może dodam III sposób ( rysunek 18:58) AD,BE,CF − środkowe ΔABC, 1) punkt przecięcia środkowych dzieli każdą z nich w stosunku 2:1 (licząc od wierzchołka). 2)każda środkowa dzieli trójkąt na dwa trójkąty o równych polach .

	1
|OF|=		|CF|
	3

	1		1
(*) P5=P4=		PΔAFC=		PΔABC
	3		6

	1
|OD|=		|AD|
	3

	1		1
(**) P1=P3=		PΔCDA=		PΔABC
	3		6

	1
|EO|=		|EB|
	3

	1		1
(***) P2=P6=		PΔCEB=		PΔABC
	3		6

	1
Z (*) i (**) i (***)⇒P1=P2=P3=P4=P5=P6=		PΔABC
	6

Eta: Musisz rozwiązywać więcej zadań i..... będzie "mocną stroną"

bezendu: Właśnie dlatego zaczynam żeby na maturze nie było nie miłej niespodzianki tak jak z trygonometrią P.S mam już zdjęcia zaraz wrzucę zadanka

bezendu: Mila dziękuję również za rozwiązanie