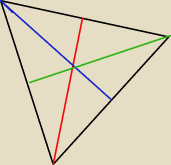
planimetria-dowód Madzik: Jak dowieść, zapisać, że wszytskie małe trójkąty, które powstają po narysowaniu środkowych trójkąta mają takie same pola?

Madzik: Pomoże ktos?

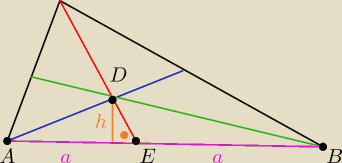
Nienor: Trójkąty ΔAED i ΔEDB mają w oczywisty sposób równej długości podstawy (połowa boku). Zauważ, też że mają tę samą wysokość (h) opuszczoną na podstawę. Stąd wniosek, że mają równe pola. Jak przeprowadzisz to rozumowanie dla pozostałych trójkątów, dojdziesz do wniosku, że wszystkie te pola muszą być sobie równe.

Madzik: Okej, o to mi właśnie chodziło, dziękuje!

Nienor:

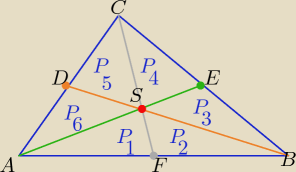
Eta: Korzystamy z własności: każda środkowa dzieli trójkąt na dwa trójkąty o równych polach zatem : ( zielona środkowa) (*)AE : P₅+P₆+P₄=P₁+P₂+P₃ ( brązowa środkowa) (**) : P₅+P₄+P₃= P₂+P₁+P₆+ środkowa FS : P₁=P₂, środkowa DS: P₆=P₅ , środkowa SE: P₄=P₃ (*) 2P₅+P₄= 2P₂+P₄ ⇒ P₅=P₂=P₁=P₆ (**) 2P₁+P₃=2P₁+P₂ ⇒ P₃=P₂ zatem P₁=P₂=P₃=P₄=P₅=P₆