trójkąty olka: podobne: w trójkącie poprowadzono środkowe, które podzieliły dany trójkąt na szećś mniejszych trójkątów. wykaż, że pola powstałych trójkątów są równe.

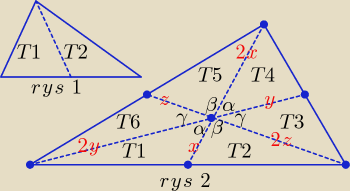
Bogdan: Znalazłem nierozwiązanie zadanie, zobaczmy, że jest banalne. Korzystamy z następujących własności: 1. Środkowa w trójkącie dzieli trójkąt na dwa trójkąty o równych polach, na rysunku 1równe pola mają trójkąty T1 i T2, na rysunku 2 równe pola mają: T1 i T2, T3 i T4, T5 i T6. 2. Środek ciężkości trójkąta, czyli punkt przecięcia środkowych, dzieli każdą środkową w stosunku 1 : 2. Zaznaczamy kąty wierzchołkowe (rys. 2): α, β, γ. Wyznaczamy pola trójkątów:

	1
T1: P1 =		x*2y*sinα = xy*sinα,
	2

	1
T4: P4 =		2x*y*sinα = xy*sinα,
	2

	1
T2: P2 =		x*2z*sinβ = xz*sinβ,
	2

	1
T5: P5 =		2x*z*sinα = xz*sinβ,
	2

	1
T3: P3 =		y*2z*sinγ = yz*sinγ,
	2

	1
T4: P6 =		2y*z*sinγ = yz*sinγ.
	2

Widzimy, że równe pola mają trójkąty T1 i T4 oraz T2 i T5 oraz T3 i T6, uwzględniając równość trójkątów pokazaną w punkcie 1 otrzymujemy: P₁ = P₄ = P₃ = P₆ = P₅ = P₂.

jimi: To co napisałeś nie udowadnia że te trójkąty mają równe pola.

Panko: Jeżeli można Wystarczy do dowodu fakcik : Jeżeli dwa trójkąty mają równe podstawy i równe wysokości opuszczone na tę podstawę to mają równe pola Stąd T6= T5 i T4=T3 i T1=T2 Dalej stosują fakcik ⇒T6+T5 +T4=T1+T2+T3 i powyższe ⇒ T6=T1 itd..... Tylko Patrz skoro są równe i suma ich pól daje całe pole to każdy ma 1/6 P