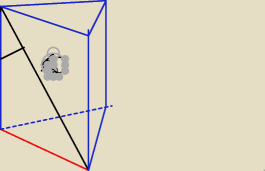
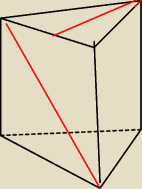
narysowany graniastosłup jest prawidłowy − oblicz długość czerwonego odcinka ,przekątna wynosi
10 ,a zaznaczony kąt ma 30 stopni .nie stosujcie funkcji trygonometrycznych
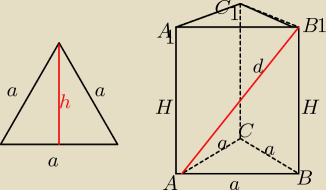
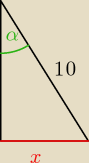α=30o
Masz taki Δ jak na rysunku powyżej. Z własności Δ prostokątnego o kątach ostrych 30o i 60o
wynikają długości boków. I tak x=połowa przeciwprostokątnej.
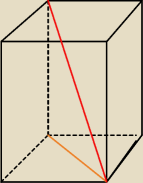oblicz pole powierzchni całkowitej narysowanego graniastosłupa prawidłowego przekątna
podstawy ma 2 pierwiastki z dwóch ,a przekątna graniastosłupa 2 pierwiastki z sześciu
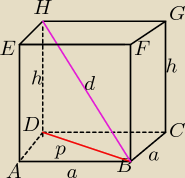p=2√2 − przekątna kwadratu (p=a√2)
a√2=2√2
a=2
d=2√6
W Δ HDB:
h2+p2=d2
h2+(2√2)2=(2√6)2
h2=4*6−4*2
h2=24−8
h2=16
h=4
Pc=2*a2+4*a*h podstaw i oblicz
oblicz pole powierzchni całkowitej narysowanego graniastosłupa prawidłowego trójkątnego o
przekątnej równej 2 pierwiastki z 41 i wysokości podstawy 4 pierwiastki z 3 .prosze was bardzo
rozwiążcie mi to
No, ja mogę rozwiązać, ale powinnaś sama coś zrobić, bo mała korzyść z odpisania.
h=4√3 −wysokość podstawy (trójkąta równobocznego)
Wzór na wysokość Δ równobocznego o boku a:
| a√3 | a√3 | |||
h= | ⇔ | =4√3 /*2 | ||
| 2 | 2 |
| a2√3 | √3 | 64√3 | ||||
PΔ= | ⇔PΔ=82* | = | ||||
| 4 | 4 | 4 |
