trygonometria
dociekliwy: | | 1 | |
mam rozwiązanie ujemne: cosx=− |
| i zastanawiam się dlaczego od π muszę odjąć i dodać to |
| | 2 | |
wyrażenie, aby wyszły mi rozwiązania. nie rozumiem tej zasady, czy mógłby ktoś objaśnić?
jak sobie radzicie z rozwiązaniami tego typu, słyszałem o prostej pomocniczej o przeciwnym
współczynniku, ale nie bardzo wiem jak to miałoby wyglądać.
dzięki
1 maj 15:44
Janek191:
więc
| | 2 | | 4 | |
x = |
| π + 2π*k ∨ x = |
| π + 2π*k, gdzie k − liczba całkowita |
| | 3 | | 3 | |
1 maj 16:48
Janek191:
więc
| | 2 | | 4 | |
x = |
| π + 2π*k ∨ x = |
| π + 2π*k, gdzie k − liczba całkowita |
| | 3 | | 3 | |
1 maj 16:48
dociekliwy: tak, tak dzięki, ale chodzi mi o zasade przy ujemnych rozwiązaniach, w jaki sposób się to
wszystko wylicza i dlaczego
1 maj 18:36
patagończyk z erytrei: podbijam
1 maj 19:09
dociekliwy: odstawcie grillowanie i pomóżcie

1 maj 19:54
dociekliwy: ponawiam prośbę
1 maj 23:29
dociekliwy: SZYBCIEJ
1 maj 23:40
Mila:
| | 1 | |
Dla równania cosx= |
| masz serię rozwiązań: |
| | 2 | |
| | 1 | |
Dla równania cosx=− |
| masz serię rozwiązań: |
| | 2 | |
| | π | | π | |
x1= |
| +π+2kπ lub x2=− |
| +π+2kπ ⇔ |
| | 3 | | 3 | |
| | 4π | | 2π | |
x1= |
| +2kπ lub x2= |
| +2kπ |
| | 3 | | 3 | |
1 maj 23:46
dociekliwy: a czy niezależnie od wartości kosinusa (podstawowe kąty), jeśli jest on ujemny to dodaję π?
2 maj 00:13
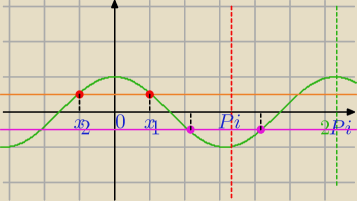
Mila: Najpierw wyznacz serię rozwiązań dla cos dodatniego, popatrz na wykres ( czerwone punkty).
potem, jak zapisałam.
II sposób
Możesz wyznaczyć tylko
| | −1 | |
a dla cosx= |
| ( ujemnego) |
| | 2 | |
2 maj 00:23
gerard: | | √2 | |
tak to łapię w stu procentach, pytam tylko o to czy dla np. cosx=− |
| i w innych |
| | 2 | |
przypadkach ujemnego rozwiązania też będę musiał odejmować lub dodawać do "π"?

2 maj 00:33
Mila: Tak. To wynika z wzorów redukcyjnych.
2 maj 00:36
gerard: a na jakiej zasadzie, jesli można jeszcze o to dopytać?
2 maj 00:39
Cusack: spróbuję wyjaśnić nieco inaczej.
co trzeba wiedzieć:
−cosinus przyjmuje ujemne wartości w II i III ćwiartce układu współrzędnych
−podstawowy okres cosinusa wynosi 2π
−funkcja cosinus jest parzysta
Najpierw szukamy rozwiązania ogólnego równania w przedziale <0;π>
właśnie w tym przedziale, bo cosinus przyjmuje w nim swoje wszystkie wartości.
−−−−−
Dla sinusa będzie to inny przedział (jaki?)
−−−−−−
szukamy rozw. ogólnego w przedziale <0;π> i dodatkowo wiemy, że cosinus jest dodatni w I
| | π | |
ćwiartce. Zatem zostaje tylko przedział < |
| ;π> |
| | 2 | |
x
0 − rozw. ogólne
| | π | | 1 | | π | |
odejmujemy |
| , bo cosx= |
| dla x= |
| |
| | 3 | | 2 | | 3 | |
więc
drugie rozwiązanie mamy od razu, bo cosinus jest parzysty:
2 maj 00:39
Cusack: spóźniłem się trochę, ale może się przyda.
pozdrawiam

2 maj 00:40
gerard: przyda się, trygonometrie muszę miec jako tako opanowaną bo u mnie na studiach też będzie w
szerokim zakresie, dzięki Mila&Cusack
2 maj 00:43
gerard: DZIĘKI

przydało się dzisiaj na maturze

zapamiętałem, ale chciałbym wiedzieć jeszcze na jakiej zasadzie to wynika z wzorów
redukcyjnych.
10 maj 18:30
ZKS:
Ponieważ sin(x) = sin(180o − x).
10 maj 18:36
Mila:
Gerard, to miło, że pomoc przydała się.
Po maturze zabieraj się za analizę matematyczną.Koniecznie uzupełnij i rozszerz wiadomości z
trygonometrii.
10 maj 18:51
gerard: okej, właśnie planuję wziąć jakieś korki na wakacje. a czy słyszałaś coś o kalkulatorze
ti−nspire? czy opłaca się zakupić taki sprzęcik czy jednak lepiej pomyśleć o wolframie?
10 maj 18:57
Mila:
Na to pytanie, to lepiej odpowie Ci ZKS i Trivial.
Korepetycje nie są Ci już potrzebne, ale praca własna, zawsze możesz skorzystać z naszej
pomocy.
10 maj 19:04
ZKS:
Na co Ci taki kalkulator?
10 maj 19:08
gerard: Zakładam, że nie będzie to zabawka ani narzędzie do zwyczajnych wyliczeń, a raczej sprzęt,
który pomoże mi lepiej zrozumieć jak zachowują się funkcje, bez konieczności używania kartki
papieru czy też internetu jeśli nie będzie takiej możliwości.
10 maj 20:32
natttt:
14 maj 21:05
natttt:
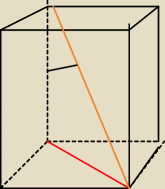
oblicz pole powierzchni całkowitej narysowanego graniastosłupa prawidłowego krawędz boczna tego
graniastosłupa wynosi 4 ,zaznaczony kąt ma 30 stopni ,prosze pomóżcie
14 maj 22:23
natttt:
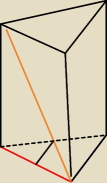
oblicz pole Pc tego graniastosłupa prawidłowego .przekątna wynosi 9 ,a zaznaczony kąt ma miare
45 stopni
14 maj 22:30
natttt:
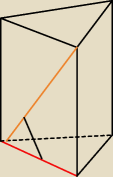
oblicz Pc tego graniastosłupa prawidłowego ,krawędz podstawy 2 ,zaznaczony kąt 60 stopni
14 maj 22:36
natttt:
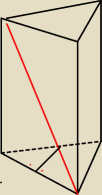
oblicz Pc tego graniastosłupa prawidłowego ,przekątna wynosi 8 ,a zaznaczony kąt ma 60 stopni
14 maj 22:41
natttt: prosze pomóżcie bo naprawdę z geometrią u mnie to ciężko bardzo prosze
14 maj 22:42
natttt: prosze pomóżcie
14 maj 22:48
Mila:
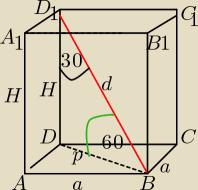
1) Graniastosłup czworokątny.
A sama nic nie zrobisz?
Nie rysuj wszystkiego naraz, bo źle się rozwiązuje.
Zadania wpisuj w pojedynczych postach.
Δ D
1DB jest połową Δ równobocznego o boku d
H =4 jest wysokością w tym Δ
Policzymy z tw. Pitagorasa
d
2=p
2+H
2
(2p)
2=p
2+4
2
4p
2=p
2+16
3p
2=16
obliczamy a
p=a
√2 przekątna kwadratu,porównujemy wzory
| | 8 | | 2√6 | | 16 | | 32√6 | |
Pc=2* |
| +4* |
| *4= |
| + |
| |
| | 3 | | 3 | | 3 | | 3 | |
14 maj 23:19
Mila:
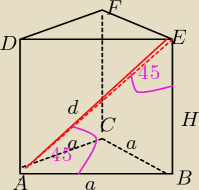
d=9
ΔABE jest Δ prostokątnym równoramiennym ( kąty ostre po 45
0)
H=a
d
2=a
2+a
2
9
2=2a
2
81=2a
2
| | 81 | |
a2= |
| / pierwiastkujemy |
| | 2 | |
| | 81 | | √3 | | 81√3 | | 9√2 | | 9√2 | |
Pc=2* |
| * |
| +3*a*H= |
| + |
| * |
| |
| | 2 | | 4 | | 4 | | 2 | | 2 | |
| | 81√3 | | 3*81√3 | |
Pc= |
| + |
| =81√3 |
| | 4 | | 4 | |
14 maj 23:32
Mila:
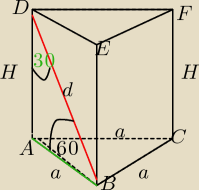
a=2
ΔDAB jest połową Δ równobocznego o boku d
H jest wysokością, możesz obliczyć z tw. Pitagorasa (4
2=2
2+H
2) albo gotowego wzoru:
H=2
√3
P
c=2*
√3+3*a*H=2
√3+3*2*2
√3
P
c=2
√3+12
√3
P
c=14
√3
Ostatnie rozwiąż sama
a=4
14 maj 23:44
natttt: dzięki obliczyłam
15 maj 00:14
Mila: 
15 maj 00:15
natttt: wyszło mi 56 pierwiastek z 3
15 maj 00:16
Mila: Zgadza się.
15 maj 00:18




 przydało się dzisiaj na maturze
przydało się dzisiaj na maturze  zapamiętałem, ale chciałbym wiedzieć jeszcze na jakiej zasadzie to wynika z wzorów
redukcyjnych.
zapamiętałem, ale chciałbym wiedzieć jeszcze na jakiej zasadzie to wynika z wzorów
redukcyjnych.
 oblicz pole powierzchni całkowitej narysowanego graniastosłupa prawidłowego krawędz boczna tego
graniastosłupa wynosi 4 ,zaznaczony kąt ma 30 stopni ,prosze pomóżcie
oblicz pole powierzchni całkowitej narysowanego graniastosłupa prawidłowego krawędz boczna tego
graniastosłupa wynosi 4 ,zaznaczony kąt ma 30 stopni ,prosze pomóżcie
 oblicz pole Pc tego graniastosłupa prawidłowego .przekątna wynosi 9 ,a zaznaczony kąt ma miare
45 stopni
oblicz pole Pc tego graniastosłupa prawidłowego .przekątna wynosi 9 ,a zaznaczony kąt ma miare
45 stopni
 oblicz Pc tego graniastosłupa prawidłowego ,krawędz podstawy 2 ,zaznaczony kąt 60 stopni
oblicz Pc tego graniastosłupa prawidłowego ,krawędz podstawy 2 ,zaznaczony kąt 60 stopni
 oblicz Pc tego graniastosłupa prawidłowego ,przekątna wynosi 8 ,a zaznaczony kąt ma 60 stopni
oblicz Pc tego graniastosłupa prawidłowego ,przekątna wynosi 8 ,a zaznaczony kąt ma 60 stopni
 1) Graniastosłup czworokątny.
A sama nic nie zrobisz?
Nie rysuj wszystkiego naraz, bo źle się rozwiązuje.
Zadania wpisuj w pojedynczych postach.
Δ D1DB jest połową Δ równobocznego o boku d
1) Graniastosłup czworokątny.
A sama nic nie zrobisz?
Nie rysuj wszystkiego naraz, bo źle się rozwiązuje.
Zadania wpisuj w pojedynczych postach.
Δ D1DB jest połową Δ równobocznego o boku d
 d=9
ΔABE jest Δ prostokątnym równoramiennym ( kąty ostre po 450)
H=a
d2=a2+a2
92=2a2
81=2a2
d=9
ΔABE jest Δ prostokątnym równoramiennym ( kąty ostre po 450)
H=a
d2=a2+a2
92=2a2
81=2a2
 a=2
ΔDAB jest połową Δ równobocznego o boku d
a=2
ΔDAB jest połową Δ równobocznego o boku d
