Matura rozszerzona poprawkowa 2009
Kuba: Zamieszcze zadania które pamiętam

25 sie 12:18
Kuba: a1 = x
a2 = 4x − 1
a1 + a2 + a3 + a4 + a5 = 25
jest to ciąg arytmetyczny gdzie n≥1
oblicz x i sume od a11 − a25
25 sie 12:21
Kuba: prosze kogoś o rozwiązywanie tych zadań

25 sie 12:22
Kuba: y + 2x − 1 = 0
znajdź najmniejszą wartość punktu A jaką przyjmuje kwadrat odległości od osi.
Punkt A znajduje się na tej prostej.
25 sie 12:28
Kuba:
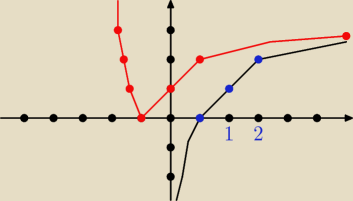
podaj wzór funkcji logarytmicznej (tej na rysunku)
trzeba było narysować funkcje g(x)=|f(x) − 2| ( ja narysowałem tak (wykres czerwony)
i trzeba było z wykresy rozwiązać nierówność f(x)≥g(x)
25 sie 12:36
Kuba: 7 osób z Basią i Jackiem wybrało się do kina, w jednym rzędzie siadają. Na ile sposobów można
rozmieścić te 7 osób tak żeby Basia i Jacek siedzieli obok siebie?
I jakie jest prawdopodobieństwo rozmieszczenia tych 7 osób tak żeby basia nie siedziała obok
jacka?
25 sie 12:43
Kuba:
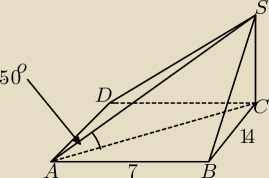
Nie pamiętam zabardzo treści ale pamiętam rysunek.
W podstawie ostrosłupa jest prostokąt gdzie |AB| = 7 a |BC| = 14
Krawędź CS jest prostopadła do podstawy.
Kąt najdłuższej krawędzi do podstawy wynosi 50
o
oblicz jego objętość.
rysunku nie było trzebabyło go narysować.
25 sie 12:51
Kuba: wiem że doszedłem do takiej prostej y = − √3 x + 6√3 + 18
i miałem napisać wzór nierówności gdzie A zawiera się w półpłaszczyźnie tej prostej.
A=(√10, 28)
i ja napisałem
y<− √3 x + 6√3 + 18
25 sie 12:54
Kuba: y = x2 − mx + m + 3
dana jest funkcja kwadratowa (powyżej) mamy znaleźć 2 pierwiastki takie że suma odwrotności
tych pierwiatków jest mniejsza od zera.
25 sie 13:00
Kuba: i jeszcze był trójkąt prostokątny gdzie kąty α i β są kątami ostrymi i musimy udowodnić
tgα + tgβ ≥ 2
25 sie 13:01
AS: Zadanie 1.
a1 = x .
a2 = 4*x − 1 , r = a2 − a1 = 4*x − 1 −x = 3*x − 1
a3 = a2 + r = 4*x − 1 + 3*x − 1 = 7*x − 2
a4 = a3 + r = 7*x − 2 + 3*x − 1 = 10*x − 3
a5 = a4 + r = 10*x + 3 + 3*x − 1 = 13*x − 4
Z warunków w zadaniu
a1 + a2 + a3 + a4 + a5 = 25
35*x − 10 = 25 ⇒ 35*x = 35 ⇒ x = 1
Szukany ciąg to: 1 , 3 , 5 , 7 , 9 w którym a1 = 1 , r = 2
a25 = a1 + 24*r = 1 + 24*2 = 49
Suma wyrazów S25 = 25/2*(1 + 49) = 25*50/2 = 625
25 sie 13:03
Kuba: 4 zadań nie pamiętam... jak mi się przypomni to napisze

A prosze kogoś o rozwiązanie tych 8
co podałem.
25 sie 13:03
Kuba: AS tzn trzeba było policzyć sume od a
11 do a
25
ale x wyszedł mi taki jak Tobie

jedno chociaż narazie dobrze

25 sie 13:06
AS: Jeżeli punkt A znajduje się na prostej y + 2*x − 1 = 0 to odległością
tego punktu od osi Ox jest rzędna tego punktu,a w naszym przypadku
y = 1 − 2*x.
Kwadrat odległości
d = y
2 = (1 − 2*x)
2 = 1 − 4*x + 4*x
2
Jest to parabola o równaniu y = 4*x
2 − 4*x + 1
Minimum znajduje się w wierzchołku paraboli
a = 4 , b = −4 , c = 1
Najmniejsza wartość
ymin = 1 − 2*(1/2) = 1 − 1 = 0
25 sie 13:11
Kuba: nie wiem czy dalej te zadanie będzie dobrze jak odległość była napisana od OSI czyli nie Ox i
Oy?;> czy wystarczy od Ox?
25 sie 14:32
Kuba: aaa i ten rysunek gdzie są funkcje logarytmiczne ta 1 i 2 przesuneły mi się w prawo...czyli na
1 powinna już być 2 a po lewej od 1 powinna być własnie 1.
25 sie 14:41
Eta:
zad. z prawdopodobieństwem.
1/ zd. A −−− B i J siedzą obok siebie
to B, J −−− rozmieszczamy na 2! −− sposobów bo B,J i J,B
tak mogą przemieszczać się na pięciu miejscach czyli 5*2! sposobów
pozostałych pięć osób może się przemieszczać
też na pięciu miejscach czyli na 5!sposobów
zatem : moc A = 5*2!*5!= 10*5! = 1200 sposobów
Odp: Jeżeli Basia i Jacek siedzą obok siebie to takich ustawień jest
1200
2/
wprowadzamy zd. przeciwne do A
A
' −−− Basia i Jacek nie siedzą obok siebie
to mocA
' = mocΩ − mocA = 7! − 10*5! = 5!( 6*7 − 10) = 30*5!
zatem :
| | mocA' | | 30 | | 30 | | 15 | |
P(A') = |
| = U30*5!}{7!} = |
| = |
| = |
|
|
| | mocΩ | | 6*7 | | 42 | | 21 | |
odp: Prawdopodobieństwo tego,że Basia i Jacek nie siedzą obok siebie
wynosi
1521
25 sie 14:42
Kuba:
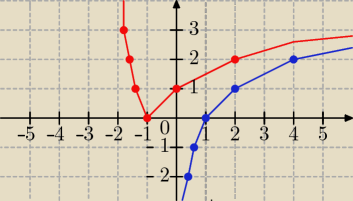
dobra narysuje jeszcze raz

bo tam jest jeszcze jeden błąd
to do tych logarytmów
niebieski to f(x)
czerwony to g(x) (oczywiscie według mnie) bo trzebabyło narysować.
25 sie 14:49
Kuba: jest czyli prawdopodobieństwo to
1521 =
57 tyle ile mi wyszło

yeah

ale co do
ilości sposobów mi wyszło 120

(policzyłem 1 * 1 * 5!)
25 sie 14:52
Eta: Przepraszam , ale pomyłkowo wpisałam ,że zmieniaja się na 5 −− ciu miejscach ,
a powinno być oczywiście ,że na
6 −ciu miejscach.
zatem błąd mi się wkradł przy przepisywaniu .
moc A =
6*2!*5! =
12*120= 1440
1/ odp;
1440 sposobów
2) już analogicznie:
mocA
' = 7! − 12*5! = 5!( 42 − 12) = 30*5!
25 sie 14:59
Eta:
no tak , oczywiście nie skróciłam
25 sie 15:00
Kuba: policze dla innych tą Sume od a
11 do a
25
razem jest tych wyrazów 25 − 10 = 15
a
11 = 1 + 10r = 1 + 20 = 21
| | 21 + 49 | |
S15 = |
| * 15 = 525
|
| | 2 | |
Więc ja chyba popełnilem jakiś błąd rachunkowy przy tej sumie nawet

25 sie 15:00
Bogdan:
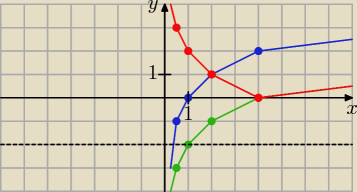
f(x) = log
ax
f(2) = 1 ⇒ log
a2 = 1 ⇒ a
1 = 2 ⇒ a = 2
f(x) = log
2x (niebieska linia)
→
wektor przesunięcia w = [0, −2]
f(x) − 2 = log
2x − 2 (zielona linia)
g(x) = |log
2x − 2| (czerwona linia)
25 sie 15:06
Kuba: ehhh czyli tylko podałem poprawnie wzór funkcji f(x)

25 sie 15:19
Bogdan:
Nie było f(x + 2), ale było f(x) − 2, czyli wykres f(x) o dwie jednostki w dół.
25 sie 15:21
Kuba: już rozumiem coś mi głupiego do głowy strzeliło że się tak wyrwałem z tym w lewo...

25 sie 15:24
Kuba: nie pomyślałem też z tymi sposobami bo mogłem po prostu 5040 odjąć 3600 = 1440
a prawdopodobieństwo dobrze mi wyszło...
25 sie 15:28
Kuba: Może ktoś pisał też z rozszerzonej poprawke?
Może mam jakiś błąd w zapamiętanych i napisanych tych zadaniach tutaj?
Może ktoś pamięta 4 pozostałe zadania?
Jak pisałeś jakie miałeś(aś) wyniki?
25 sie 17:12
AS: Aneks do zadania − przeoczyłem zapis a
11
a
10 = a1 + 9*r = 1 + 9*2 = 19
| | 10 | |
S10 = |
| *(a1 + a10) = 5*20 = 100 |
| | 2 | |
S = S25 − S10 = 625 − 100 = 525
25 sie 17:20
Kuba: no tak też można

dzięki AS
25 sie 17:25
Kuba: Może ktoś pisał też z rozszerzonej poprawke?
Może mam jakiś błąd w zapamiętanych i napisanych tych zadaniach tutaj?
Może ktoś pamięta 4 pozostałe zadania?
Jak pisałeś jakie miałeś(aś) wyniki?
25 sie 17:45
martoos: Do zadania z prosta 2x+y−1=0 zadanie brzmiało tak: Znajdz współrzedne punktu A leżacego na
prostej 2x+y−1=0 tak aby suma kwadratów odległosci punktu A od osi układu współrzednych była
najmniejsz.
25 sie 17:49
martoos: kolejne zadanie. Wykaż , że w trójkacie prostokątnym gdzie α iβ sa kątami ostrymi, to tgα +
tgβ≥2
25 sie 17:51
martoos: trapez ABCD gdzie AB || CD jest opisany na okregu o promieniu r. Przekątna AC jest nachylona do
podstawy AB pod katem α. Oblicz obwód tego trapezu w zaleznosci od kata α i prominia r
25 sie 17:53
martoos: Podaj ile miejsc wspolnych ma okrag o rownaniu x2+y2−2x−6y=0 z prosta do ktorej naleza
punkty M=(2009,4012) i N (−50;−106).
25 sie 18:00
martoos: i poprawiam zadanie

o rysunku ostrosłupa..Trzeba bylo narysowac. Przynajmniej ja to tak
odebralam
P.S z Gory przepraszam za błedy w pisowni

pisze w pospiechu
25 sie 18:09
martoos: wiem że doszedłem do takiej prostej y = − √3 x + 6√3 + 18
i miałem napisać wzór nierówności gdzie A zawiera się w półpłaszczyźnie tej prostej.
A=(√10, 28)
i ja napisałem
y<− √3 x + 6√3 + 18
Tu bład były dane punkty A (niepamietam wspoł) B(niepamietam wspoł) i C (−{10},26) było trzeba
za pomoca nierownosci opisac polplaszczyze ograniczona prosta zawierajaca punkty A i B oraz
zawierajaca punkt C..mnie wyszlo y< −{3}x+20 O ile dobrze pamietam..

wyznaczylam rownanie
prostej zawierajacej punkty A i B nastepnie sprawdzilam czy punkt c zawiera sie pod czy nad
wykresem funcji i wykazalam nierownosc
25 sie 18:18
Kuba: Marta ja właśnie gdzieś już wyżej napisałem że trzeba było go narysować, i ja go narysowałem bo
tyle pamiętałem i z rysunku przypominałem sobie jakie były polecenia

25 sie 21:11
Kuba: Heh ja zrobiłem to samo Marta z tą prostą przechodzocą przez punkt a A i B i ta prosta
wyznaczała półpłaszczyzne w której zawiera się punkt C, no ale na to czy pod czy nad sami
musieliśmy wpasć.
To nie dobrze że mamy rózne proste bo ktoś z nas napewno ma źle:(
25 sie 21:15
martoos: i wlasnie to mnie marwii

25 sie 23:09
martoos: Poprawka:
y = x2 − mx + m + 3
dana jest funkcja kwadratowa (powyżej) mamy znaleźć 2 pierwiastki takie że suma odwrotności
tych pierwiatków jest mniejsza od zera.
wyznacz wszytkie wartpsci prametru m dla ktorych rownanie ( powzej) ma dwa rozne pierwiatki
takie ze suma odwrotnosci tych pierwiatskow jest mniejsza od 1
25 sie 23:15
Bogdan:
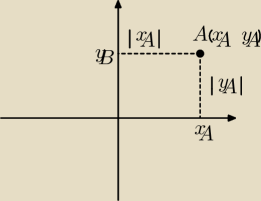
Zadanie.
Znajdź współrzędne punktu A leżącego na prostej 2x+y−1=0 tak, aby suma kwadratów
odległości punktu A od osi układu współrzędnych była najmniejsza.
Rozwiązanie.
2x + y − 1 = 0 ⇒ y = 1 − 2x
Punkt A = (x
A, y
A)
|x
A| − odległość punktu A od osi y, |y
A| − odległość punktu A od osi x.
z = |x
A|
2 + |y
A|
2 → min
z = x
A2 + y
A2 i y
A = 1 − 2x
A
z = x
A2 + (1 − 2x
A)
2 → z = x
A2 + 1 − 4x
A + 4x
A2
z(x
A) = 5x
A2 − 4x
A + 1
Funkcja z(x
A) jest funkcją kwadratową, której wykres jest parabolą ramionami
| | 4 | | 2 | |
skierowanymi w górę, posiadającą minimum dla xA = |
| = |
| . |
| | 2*5 | | 5 | |
| | 2 | | 1 | |
yA = 1 − 2xA = 1 − 2* |
| = |
| |
| | 5 | | 5 | |
25 sie 23:31
Bogdan:
Suma odwrotności pierwiastków (wzory Viete'a):
| | 1 | | 1 | | x1 + x2 | | | | −b | |
Δ ≥ 0 i |
| + |
| = |
| = |
| = |
| |
| | x1 | | x2 | | x1*x2 | | | | c | |
25 sie 23:35
Eta:
a) y = x
2 −mx +m +3
musi być spełniony układ warunków:
1/ Δ≥0
po sprowadzeniu do wspólnego mianownika i zastosowaniu wzorów Viete
'a otrzymamy:
| | x2 +x1 | | −ba | | −b | |
to: |
| = |
| = |
|
|
| | x1*x2 | | ca | | c | |
zatem drugi warunek jest:
ad1) Δ= m
2 −4m −12
to Δ≥0 <=> m
2 −6m −12≥0 <=> ( m−6)(m +2) ≥0 <=> m∊(− ∞, −2 > U < 6,∞)
ad2/
| | −b | | m | |
|
| <0 <=> |
| <0 , przy załozeniu ,że m ≠ −3
|
| | c | | m+3 | |
mamy: m( m +3) <0 <=> m∊( −3, 0 )
wybierając cz. wspólną obydwu warunków otrzymamy:
odp: m⊂( −3, 2 >
przykład b) podobnie:
1/ Δ>0 −−− bo pierwaiastki maja być różne
wyznacz teraz ten przedział..... już z pewnością potrafisz .
25 sie 23:43
Eta: 
25 sie 23:44
Bogdan:
Dobry wieczór Eto

Jak oceniasz zadania z matury poprawkowej, czy były łatwe?
Moim zdaniem były dość proste, ale niektóre wymagały jednak trochę pomyślunku, ale
tylko trochę.
25 sie 23:52
Eta:
Witam Bogdanie

Podobnie i moim zdaniem ,zadania nie były trudne.
Spodziewałam się ,że będą trudniejsze.
Jeżeli chodzi o "pomyślunek" , to bardzo dobrze ,że układający zadania
przede wszystkim kładą nacisk na logiczne myślenie.
W matematyce logiczne myślenie to 3/4 sukcesu ,a o to przecież chodzi .
Jak sam tu często pisałeś ; " to egzamin dojrzałości "

26 sie 00:12
martoos: tak w pierwszym zamiast −b/c napialam −bc:( a wszytko dlatego ze nie pisalam po koli tylko w
glowie liczylam..

a mam nadzieje ze duzo punktow mi nie ucieknie
26 sie 08:58
Kuba: no mi na maturze wyszedł przedział od −3 do plus nieskończoności ale od razu po prostu
policzyłem chyba sume odwrotności tych pierwiastków mniejszych od zera...
−bc < 0
m(m+3) < 0
i nie wiem skąd mi wyszedł taki przedział i czy on jest dobrze m∊ (−3, +∞)
26 sie 13:18
Kuba: nie pamietam czyy miało być mniejsze od zera czy od 1

26 sie 13:19
Kuba: Eta i Bogdanie rozwiążecie reszte ?;>
26 sie 13:20
Bogdan:
Kubo, zapisz pozostałe zadania w pełnej treści w oddzielnym poście, pomożemy rozwiązać.
26 sie 13:27
Kuba: no pełnej treści nie pamiętam, i tak o dziwo zapamiętałem 8 na 12 zadań

no ale dobra wstawie w odzielne posty to co jest jeszcze nie zrobione

jaki powinien być końcowy przedział w sumie odwrotności tych pierwiastków?
26 sie 13:31
Kuba: 1. było z odwrotnością tych pierwiastków. (zrobione)
2. było z prostą i punktem gdzie suma kwadratów odległości od osi(zrobione)
3. z logarytmami (zrobione nie do końca)
Czyli pierwsze pytanie z tą nierówności logarytmiczną.
Bogdanie trzeba było na podstawie wykresu rozwiązać nierówność f(x) ≥ g(x), jak to rozwiązać?
Na to narazie nowego wątku nie otworze...

26 sie 13:38
Bogdan:
Podziwiałem Kubo Twoją pamięć, czekamy na to, co pamiętasz w innym poście.
26 sie 13:39
Bogdan:
Podaj treść zadania, a nie jego nr.
26 sie 13:42
Kuba: O i Marto pamiętasz dalej kolejność tych zadań?;>
4. chyba było żeby wykazać tgα + tgβ ≥ 2
Więc nowy wątek będzie dla tego zadania

26 sie 13:46
Bogdan:
Czy chodzi o α i β w trójkącie prostokątnym?
26 sie 13:48
Kuba: ale Bogdanie (rozwiązałeś to zadanie, jedyne w tym wątku z logarytmami i wykresem)

i na podstawie tego wykresy mieliśmy rozwiązać nierówność f(x) ≥ g(x), jak to rozwiązać?
Zamieszczam je tutaj bo tu jest ten wykres

26 sie 13:51
Kuba: tak chodzi o te kąty, dla trójkąta prostokątnego(już powstał oddzielny wątek)
26 sie 13:53
Bogdan:
Ok.
f(x) = log
2x
g(x) = |log
2x − 2|
f(x) ≥ g(x) ⇔ log
2x ≥ |log
2x − 2| ⇒ |log
2x − 2| ≤ log
2x
Założenia:
1. x > 0
2. log
2x ≥ 0 ze względu na wartość bezwzględną (przypominam, jeśli |wyrażenie| ≤ a,
to a ≥ 0)
log
2x ≥ 0 ⇒ log
2x ≥ log
21 ⇒ x ≥ 1
Z założeń: x > 0 i x ≥ 1 otrzymujemy: x ≥ 1.
|log
2x − 2| ≤ log
2x
−log
2x ≤ log
2x − 2 ≤ log
2x ⇒ log
2x
−1 ≤ log
2x − log
24 ≤ log
2x
| | 1 | | x | |
log2 |
| ≤ log2 |
| ≤ log2x |
| | x | | 4 | |
Po rozwiązaniu tego układu nierówności i uwzględnieniu założenia: x ≥ 1
otrzymujemy odp.: x ≥ 2
Można jednak odczytać rozwiązanie z rysunku, patrzymy, gdzie wykres funkcji f(x)
(niebieska linia) pokrywa się z wykresem g(x) (czerwona linia) oraz gdzie
niebieski wykres jest nad czerwonym wykresem. Stwierdzamy, że f(x) ≥ g(x) dla x ≥ 2.
26 sie 14:26
martoos:
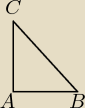
Z tw Pit: |AB|
2 + |AC|
2 = |BC|
2 (wł. trójkata prostokątnego) kąt ABC = α kąt ACB=β
tgα=|AC|/|AB|
tgβ=|AB|/|AC|
tgα+tgβ≥2
|AC|/|AB| + |AB|/|AC|≥2≥
|AC|
2+|AB|
2/|AC||AB|≥2 i teraz moment kulminacyjny czyli wyjasnienie slowne dlaczego ta
nierownosc jest spelniona.Powiem szczerze ze nie dokonca potrafilam to dowiesc.. oczywiscie
napisalam ze |AB|,|AC|,|BC| przymuja wartosci wieksze od zera (dodatnie) poniewaz sa bokami
trójkata i teraz nie mam zielonego pojecia czy to co napisze zaraz jest poprawne.., ze
najmniejsza mozliwa warosci dla tych bokow jest liczba 1 i wykazalam (poprzez podstawienie) ze
ta nierownosc jest prawdziwa.
27 sie 00:21
Sabin:
Pomnóż przez |AC||AB| i przenieś wszystko na lewą stronę. Po lewej stronie będziesz miała
rozwinięty wzór skróconego mnożenia, czyli lewa strona ≥ 0 i już.
27 sie 00:25
martoos: no faktycznie ..dzieki

29 sie 13:11
18 lis 17:35
xDeee: β
∞∞∞NauKa pisma xDe Nie no normalka Ggg xDdeee


18 lis 17:36
18 lis 17:38


 podaj wzór funkcji logarytmicznej (tej na rysunku)
trzeba było narysować funkcje g(x)=|f(x) − 2| ( ja narysowałem tak (wykres czerwony)
i trzeba było z wykresy rozwiązać nierówność f(x)≥g(x)
podaj wzór funkcji logarytmicznej (tej na rysunku)
trzeba było narysować funkcje g(x)=|f(x) − 2| ( ja narysowałem tak (wykres czerwony)
i trzeba było z wykresy rozwiązać nierówność f(x)≥g(x)
 Nie pamiętam zabardzo treści ale pamiętam rysunek.
W podstawie ostrosłupa jest prostokąt gdzie |AB| = 7 a |BC| = 14
Krawędź CS jest prostopadła do podstawy.
Kąt najdłuższej krawędzi do podstawy wynosi 50o
oblicz jego objętość.
rysunku nie było trzebabyło go narysować.
Nie pamiętam zabardzo treści ale pamiętam rysunek.
W podstawie ostrosłupa jest prostokąt gdzie |AB| = 7 a |BC| = 14
Krawędź CS jest prostopadła do podstawy.
Kąt najdłuższej krawędzi do podstawy wynosi 50o
oblicz jego objętość.
rysunku nie było trzebabyło go narysować.
 A prosze kogoś o rozwiązanie tych 8
co podałem.
A prosze kogoś o rozwiązanie tych 8
co podałem.
 jedno chociaż narazie dobrze
jedno chociaż narazie dobrze
 dobra narysuje jeszcze raz
dobra narysuje jeszcze raz bo tam jest jeszcze jeden błąd
to do tych logarytmów
niebieski to f(x)
czerwony to g(x) (oczywiscie według mnie) bo trzebabyło narysować.
bo tam jest jeszcze jeden błąd
to do tych logarytmów
niebieski to f(x)
czerwony to g(x) (oczywiscie według mnie) bo trzebabyło narysować.
 yeah
yeah ale co do
ilości sposobów mi wyszło 120
ale co do
ilości sposobów mi wyszło 120 (policzyłem 1 * 1 * 5!)
(policzyłem 1 * 1 * 5!)


 f(x) = logax
f(2) = 1 ⇒ loga2 = 1 ⇒ a1 = 2 ⇒ a = 2
f(x) = log2x (niebieska linia)
→
wektor przesunięcia w = [0, −2]
f(x) − 2 = log2x − 2 (zielona linia)
g(x) = |log2x − 2| (czerwona linia)
f(x) = logax
f(2) = 1 ⇒ loga2 = 1 ⇒ a1 = 2 ⇒ a = 2
f(x) = log2x (niebieska linia)
→
wektor przesunięcia w = [0, −2]
f(x) − 2 = log2x − 2 (zielona linia)
g(x) = |log2x − 2| (czerwona linia)


 dzięki AS
dzięki AS
 o rysunku ostrosłupa..Trzeba bylo narysowac. Przynajmniej ja to tak
odebralam
P.S z Gory przepraszam za błedy w pisowni
o rysunku ostrosłupa..Trzeba bylo narysowac. Przynajmniej ja to tak
odebralam
P.S z Gory przepraszam za błedy w pisowni pisze w pospiechu
pisze w pospiechu
 wyznaczylam rownanie
prostej zawierajacej punkty A i B nastepnie sprawdzilam czy punkt c zawiera sie pod czy nad
wykresem funcji i wykazalam nierownosc
wyznaczylam rownanie
prostej zawierajacej punkty A i B nastepnie sprawdzilam czy punkt c zawiera sie pod czy nad
wykresem funcji i wykazalam nierownosc


 Zadanie.
Znajdź współrzędne punktu A leżącego na prostej 2x+y−1=0 tak, aby suma kwadratów
odległości punktu A od osi układu współrzędnych była najmniejsza.
Rozwiązanie.
2x + y − 1 = 0 ⇒ y = 1 − 2x
Punkt A = (xA, yA)
|xA| − odległość punktu A od osi y, |yA| − odległość punktu A od osi x.
z = |xA|2 + |yA|2 → min
z = xA2 + yA2 i yA = 1 − 2xA
z = xA2 + (1 − 2xA)2 → z = xA2 + 1 − 4xA + 4xA2
z(xA) = 5xA2 − 4xA + 1
Funkcja z(xA) jest funkcją kwadratową, której wykres jest parabolą ramionami
Zadanie.
Znajdź współrzędne punktu A leżącego na prostej 2x+y−1=0 tak, aby suma kwadratów
odległości punktu A od osi układu współrzędnych była najmniejsza.
Rozwiązanie.
2x + y − 1 = 0 ⇒ y = 1 − 2x
Punkt A = (xA, yA)
|xA| − odległość punktu A od osi y, |yA| − odległość punktu A od osi x.
z = |xA|2 + |yA|2 → min
z = xA2 + yA2 i yA = 1 − 2xA
z = xA2 + (1 − 2xA)2 → z = xA2 + 1 − 4xA + 4xA2
z(xA) = 5xA2 − 4xA + 1
Funkcja z(xA) jest funkcją kwadratową, której wykres jest parabolą ramionami

 Jak oceniasz zadania z matury poprawkowej, czy były łatwe?
Moim zdaniem były dość proste, ale niektóre wymagały jednak trochę pomyślunku, ale
tylko trochę.
Jak oceniasz zadania z matury poprawkowej, czy były łatwe?
Moim zdaniem były dość proste, ale niektóre wymagały jednak trochę pomyślunku, ale
tylko trochę.
 Podobnie i moim zdaniem ,zadania nie były trudne.
Spodziewałam się ,że będą trudniejsze.
Jeżeli chodzi o "pomyślunek" , to bardzo dobrze ,że układający zadania
przede wszystkim kładą nacisk na logiczne myślenie.
W matematyce logiczne myślenie to 3/4 sukcesu ,a o to przecież chodzi .
Jak sam tu często pisałeś ; " to egzamin dojrzałości "
Podobnie i moim zdaniem ,zadania nie były trudne.
Spodziewałam się ,że będą trudniejsze.
Jeżeli chodzi o "pomyślunek" , to bardzo dobrze ,że układający zadania
przede wszystkim kładą nacisk na logiczne myślenie.
W matematyce logiczne myślenie to 3/4 sukcesu ,a o to przecież chodzi .
Jak sam tu często pisałeś ; " to egzamin dojrzałości " 
 a mam nadzieje ze duzo punktow mi nie ucieknie
a mam nadzieje ze duzo punktow mi nie ucieknie

 no ale dobra wstawie w odzielne posty to co jest jeszcze nie zrobione
no ale dobra wstawie w odzielne posty to co jest jeszcze nie zrobione jaki powinien być końcowy przedział w sumie odwrotności tych pierwiastków?
jaki powinien być końcowy przedział w sumie odwrotności tych pierwiastków?


 i na podstawie tego wykresy mieliśmy rozwiązać nierówność f(x) ≥ g(x), jak to rozwiązać?
Zamieszczam je tutaj bo tu jest ten wykres
i na podstawie tego wykresy mieliśmy rozwiązać nierówność f(x) ≥ g(x), jak to rozwiązać?
Zamieszczam je tutaj bo tu jest ten wykres
 Z tw Pit: |AB|2 + |AC|2 = |BC|2 (wł. trójkata prostokątnego) kąt ABC = α kąt ACB=β
tgα=|AC|/|AB|
tgβ=|AB|/|AC|
tgα+tgβ≥2
|AC|/|AB| + |AB|/|AC|≥2≥
|AC|2+|AB|2/|AC||AB|≥2 i teraz moment kulminacyjny czyli wyjasnienie slowne dlaczego ta
nierownosc jest spelniona.Powiem szczerze ze nie dokonca potrafilam to dowiesc.. oczywiscie
napisalam ze |AB|,|AC|,|BC| przymuja wartosci wieksze od zera (dodatnie) poniewaz sa bokami
trójkata i teraz nie mam zielonego pojecia czy to co napisze zaraz jest poprawne.., ze
najmniejsza mozliwa warosci dla tych bokow jest liczba 1 i wykazalam (poprzez podstawienie) ze
ta nierownosc jest prawdziwa.
Z tw Pit: |AB|2 + |AC|2 = |BC|2 (wł. trójkata prostokątnego) kąt ABC = α kąt ACB=β
tgα=|AC|/|AB|
tgβ=|AB|/|AC|
tgα+tgβ≥2
|AC|/|AB| + |AB|/|AC|≥2≥
|AC|2+|AB|2/|AC||AB|≥2 i teraz moment kulminacyjny czyli wyjasnienie slowne dlaczego ta
nierownosc jest spelniona.Powiem szczerze ze nie dokonca potrafilam to dowiesc.. oczywiscie
napisalam ze |AB|,|AC|,|BC| przymuja wartosci wieksze od zera (dodatnie) poniewaz sa bokami
trójkata i teraz nie mam zielonego pojecia czy to co napisze zaraz jest poprawne.., ze
najmniejsza mozliwa warosci dla tych bokow jest liczba 1 i wykazalam (poprzez podstawienie) ze
ta nierownosc jest prawdziwa.

 Zal
Zal 


 Dobra Coś trudniejszego
Ile to 2 + 2
Dobra Coś trudniejszego
Ile to 2 + 2 
 ♥
♥ 
