funkcja logarytmiczna
Kipic: walkowalem to zadanie nawet dlugo i nie moge dojsc do odpowiedzi prawidlowej
Wyznacz dziedzine funkcji
| | 2x | |
f(x) = log |
| + log0,5(1−2x) |
| | x+2 | |
oczywiscie z definicji logarytmu

wiem ze w obu przypadkach a>0 a≠0 i b>0
wiec rozwiazuje :
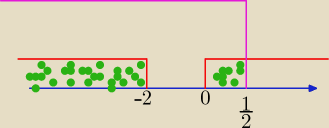
(2x)(x+2)>0 ⇒ x=0 x=−2
czyli przedzial to x∊(−∞,−2)u(0;+∞)
teraz drugi logarytm
1−2x>0
−2x>−1
| | 1 | |
czyli przedzial to x∊(−∞; |
| ) |
| | 2 | |
| | 1 | |
lacze sume przedzialow to wychodzi : x∊(−∞,−2)u(−2;0)u(0; |
| ) |
| | 2 | |
| | 1 | |
a w odpowiedzxiach jest x∊(−∞,−2)u(0; |
| ) |
| | 2 | |
i gdzie robie blad ?
27 lut 17:48
problem: a przypadkiem nie czesc wspolna? jak masz (−∞; 1/2 ) i (−∞, −2) u (0, ∞) to wychodzi jak dla
mnie (−∞;−2)u(0;1/2)
27 lut 17:56
problem: a w zalozeniach do tego a≠1 i a>0 czyli masz blad
27 lut 18:00
27 lut 18:03
asdf:
.
27 lut 18:08
27 lut 18:10
27 lut 18:10
asdf: Nie wiem o co Ci chodzi, rysuj sobie wykres bo tego nie da się ogarnąć bez rysunku (nawet jak
juz ktos ogarnia)
27 lut 18:13
Ada: D: 2x:2+x>0 część wspólna 2+x musi być rózne od 0 czesc wspolna 1−2x>0
2x>0
X>0
Xmusi byc rózne od 0 czesc wspolna x>1:2
Czyli, xe(1/2 , nieskończoność)\ {−2}
27 lut 18:13
 wiem ze w obu przypadkach a>0 a≠0 i b>0
wiec rozwiazuje :
wiem ze w obu przypadkach a>0 a≠0 i b>0
wiec rozwiazuje :
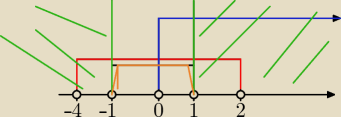 to dlacezgo tutaj w tym zadanu https://matematykaszkolna.pl/forum/189333.html czescia wspolna nie jest (0,1) skoro w odpowiedziach jest
D=(−4;−1)u(−1;0)u(0;1)u(1;2)
to dlacezgo tutaj w tym zadanu https://matematykaszkolna.pl/forum/189333.html czescia wspolna nie jest (0,1) skoro w odpowiedziach jest
D=(−4;−1)u(−1;0)u(0;1)u(1;2) 

 .
.

 ?
?