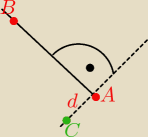
wspołrzędne punktu odleglego od danego odcinka maciek: Witam Mam taki problem: jak wyznaczyć współrzędne punktu C jeśli jest oddalony od A o d i leży na prostej prostopadłej do odcinka AB, Dane są: współrzędne A(3,1),B(3,5) i d jakie chcecie, możne być d=2 Mecze się nad tym już dwa dni. Mam nadzieje ze chociaż tutaj ktos mi pomoże. Pozdrawiam Maciek

tim: W skrócie: Znajdź równanie prostej AB. 1223 Znajdź punkt C wiedząc, że d = 2 na podstawie wzoru na odległość punktu od prostej. 1249

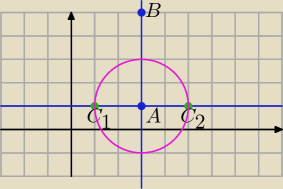
Bogdan: Jest wiele sposobów rozwiązania tego zadania, można np. zaangażować tu wektory. Pokażę sposób z okręgiem. Prosta przechodząca przez punkty: A=(3, 1) i B = (3, 5) ze względu na równość odciętych tych punktów jest równoległa do osi y i ma równanie: x = 3. Prosta do niej prostopadła i przechodząca przez punkt A jest równoległa do osi x i ma równanie: y = 1, bo rzędna punktu A ma wartość 1. Tworzymy okrąg o środku w punkcie A i promieniu d, np. d = 2: (x − 3)² + (y − 1)² = 4 Okrąg ten przecina prostą y = 1 w dwóch punktach, każdy z nich jest odległy os A o 2. Rozwiązujemy układ równań: (x − 3)² + (y − 1)² = 4 i y = 1, stąd: (x − 3)² = 4 ⇒ x − 3 = −2 lub x − 3 = 2 ⇒ x = 1 lub x = 5. Otrzymalismy dwa punkty: C₁ = (1, 1) oraz C₂ = (5, 1).

tim: Coś mi nie wyszło. Inaczej: Znajdź równanie prostej AB. Znajdź równanie prostej prostopadłej do AB przechodzącej przez AC. Znajdź punkt C wiedząc, że d = 2 na podstawie wzoru na odległość punktu od prostej. 1249 Bogdanie, coś takiego?

maciek: Dzieki za podpowiedź. Po radach Tima wpadlem jeszcze na pomysl aby jako brakujacy drugi "ogranicznik" zastosowac wzór na odległość między punktami; dla danych A=(5,1) i B=(3,3) d=√2 otrzymuje pierwsze równanie: 2=|xp+yp−8| gdzie xp i yp sa to wspolrzedne szukanego punktu. wiec jako drugie rownanie ( zeby miec układ 2 równań z 2 niewiadomymi) wykorzystuje 2=(xp−5)²+(yp−3)²; z modulu: xp+yp=10 or xp+yp = 6 jednak za kazdym razem gdy probuje wyznaczony xp podstawic do wzoru na odległość 2 punktow otrzymuje Δ<0 w sumie prawie identyczny sposob wiec chyba popelniam gdzies błąd. a mogłbym prosic o przedstawienie sposobu z wektorami ? jeszcze raz dzieki

maciek: widze ze zanim napisalem posta do konca juz sie poajwilo to o co mi chodzilo

maciek: Ok zanazlem blad u siebie. otrzymujac de facto rownanie okregu, zamiast (yp−3) powinno byc (yp−1) podtrzymuje zapytanie o wektory

AS: Ale rachunki! C1(xA−2,1) lub C2(xA+2,1) czyli C1(3−1,1) lub C2(3+1,1) C1(1,1) lub C2(5,1)

Bogdan: Spróbujmy Timie. A = (3, 1), C = (x_c, y_c), d = |AC| = 2 Równanie prostej zawierającej punkty A, B: x = 3 ⇒ x − 3 = 0

	|1*xc + 0*yc − 3|
2 =		⇒ 2 = |xc − 3| ⇒
	√12 + 02

⇒ x_c − 3 = −2 lub x_c − 3 = 2, stąd x_c = 1 lub x_c = 5. Skorzystamy teraz z wzoru na odległość między punktami i bierzemy punkty A i C. 2² = (x_c − 3)² + (y_c − 1)², dla x_c = 1: 4 = 4 + (y_c − 1)² ⇒ (y_c − 1)² = 0 ⇒ y_c = 1, dla x_c = 5: 4 = 4 + (y_c − 1)² ⇒ (y_c − 1)² = 0 ⇒ y_c = 1. Otrzymaliśmy punkty: (1, 1) oraz (5, 1).

tim: Czyli może być <yeah>

maciek: do AS: Zbytnio uproscilem zadanie wybierajac odcinek AB nie lezacy an wykresie funkcji liniowej. Chodzilo mi o uogólnioną metoda rozwiazywania tego problemu. Nastepnym utrudnioniem jest orzeczenie dla kazdych danych ( linie pod roznymi katami, pionowe, poziome) ktory z dwoch otrzymanych w ten sposób punktow lezy po lewej stronie odcinka patrzac od A do B. Tzn o jednoznaczne zweryfikowanie ktory lezy po ktorej stronie.

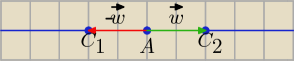
Bogdan: → → → → |w| = |−w| = 2, A = (3, 1), w = [2, 0], −w = [−2, 0] C₁ = (x₁, y₁), C₂ = (x₂, y₂) → → AC₁ = −w ⇒ [x₁ − 3, y₁ − 1 ] = [−2, 0] ⇒ x₁ − 3 = −2 i y₁ − 1 = 0 x₁ = 1 i y₁ = 1 → → AC₂ = w ⇒ [x₂ − 3, y₂ − 1 ] = [2, 0] ⇒ x₂ − 3 = 2 i y₂ − 1 = 0 x₂ = 5 i y₂ = 1

Bogdan: Jak widzisz Maćku, zadanie można rozwiązać na wiele sposobów. Sformułuj teraz w sposób czytelny problem, o którym się wypowiadasz.

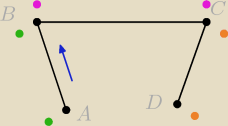
maciek: Poniewasz dla kazdego z punktow ABCD otrzymujemy parę punktow spełniających założenia, potrzebuję rozróżnić pomiedzy nimi wzgledem kierunku ruchu. Ruch adbywa sie w kierunku alfabetycznym. dane sa punkty ABCD oraz dystans od nich d. Moimi szukanymi sa współrzedne kolorowych punktów dla kazdego z odcinków. Mam nadzieje ze rozjaśniłem i dziekuję za dotychczasową pomoc.

Bogdan: Ach, ta polszczyzna.

tim: Nie wszyscy są tak mądrzy i tak idealni jak ty