Funkcja Charlize: Błagam pomóżcie mi z tym zadaniem bo mnie wytrzymam nie chce mi wyjść ... Punkty A(4,−3) B(7,1) C(5,5) są wierzchołkami trójkąta ABC a) oblicz długość wyskości trójkąta opuszczonej z wierzchołka C na bok AB b) Napisz równanie symetralnej boku AB c) Wyznacz współrzędne wierzchołka D, tak aby punkty ABCD były wierzchołkami równoległoboku. Co do podpunktu a) obliczyłam że S(5.5; −1)

tim: Rysunek do zadania. O wytłumaczenie proszę kolegę/koleżankę z forum , ja jadę do mamy. http://img2.vpx.pl/up/20090722/rysunek.gif

tim: Rysunek wykonany w programie: GEONExT.

Charlize: Nie kapuje tego ..

tim: Powoli. Spokojnie. Będzie dobrze . 1. Znajdź równanie prostej AB. 2. Znajdź równanie prostej prostopadłej do AB przechodzącej przez C. 3. Znajdź punkt przecięcia (układ równań). 4. Oblicz odległość między C i S (punktem przecięcia).

tim: b) Zapewne dziwny sposób, ale niech będzie (niech ktoś poda inny).

	1
1. Rysujesz dwa koła o tym samym promieniu (środkami są punkty A i B) (r >		|AB|).
	2

2. Miejsca ich przecięcia łączysz linią prostą − symetralna. 3. Szukasz równanie prostej prostopadłej do AB przechodzącej przez X (punkt przecięcia dwusiecznej z AB). c) 1. Znajdź równanie prostej BC. 2. Znajdź równanie prostej równoległej do BC przechodzącej przez A. 3. Znajdź równanie prostej AB. 4. Znajdź równanie prostej prostopadłej do AB przechodzącej przez C. 5. Znajdź punkt przecięcia się dwóch nowych równoległych prostych. Będzie to D.

Charlize: Nie dobra nie będe się tym katowac bo i tak tej matmy nie zdam w sierpniu ...

tim: Nie poddawaj sie Tylko nie rób tego...

Kamil: Do b moge ci podowpowiedziec

Charlize: No już trudno ja się spisałam na straty w kwietniu ... jeśli chodzi a matme ... Ale jedno mnie dziwi, że w szkole miałam 5 na koniec a matury nie zdałam ... Eh no trudno ...

Kamil: Więc tak , wyzanczasz środek odcnika AB , określasz współczynnik kierunkowy i wyznaczasz wzór na porstą prostopadła.

Kamil: Środek odcinka S(x_s;y_s) X_s = x_a+x_b _________ 2 Y_s= y_a+y_b _____________ 2

Eta: Witam do podpunktu a)

	yB − yA
piszesz równanie prostej AB: y − yB=		*( x − xB) .... bo xA ≠xB
	xB − xA

podstawiając współrzędne punktów A i B otrzymasz: prAB: 4x − 3y −25=0 teraz ze wzoru na odległość punktu C od tej prostej mamy ( zobacz wzór na str. "geom analityczna" )

	I 5*4 +5*(−3) −25I
IhABI=
	√42 +(−3)2

policz i otrzymasz długość h_AB= 4

Charlize: no to środek odcinka AB jest S(5.5; −1)

Charlize: Eta tego twojego wzoru wogole nie kapuje, ale w odpowiedziach jest tak jak ty robisz ...

Eta: b) środek odcinka AB : S( 5,5; −1) −−−− masz policzony ok teraz piszesz równanie symetralnej boku AB zatem jest to prosta prostopadła do pr.AB i przechodząca przez punktS współczynnik kierunkowy prostej AB masz z podpunktu a) tego zadania a= ⁴₃ więc −¹_a = −³₄ więc równanie symetralnej jest: y − y_S= −¹_a*( x − x_S) ....... podstaw dane i policz ( dasz już radę

Eta: kliknij tu 1223

Eta: sorry: ../strona/1223

Charlize: zostaje mi tylko sznur i do lasu ...

Eta: Jaki sznur? co Ty mówisz? Dziewczyno! Nie załamuj się , rozwiązuj zadania bez stresu Będzie dobrze , uwierz w siebie ..... ja wierzę ,że sobie poradzisz Głowa do góry! masz jeszcze sporo czasu ( no i 5 −tkę .... napewno zasłużoną) Poprostu trema Cię zjada , tak nie można! Powodzenia, jak coś to pisz , pomożemy

Charlize: Denerwuje mnie to, ze robie te zadania i mnie się wydaje, że jest dobrze a jak patrze w odpowiedzi to wynik jest całekim inny ... Normalnie szlak chce człowieka trafić ... W szkole jakoś tego nie było ... Ostatnio nawet robiłam zadania z koleżanką i ona w jednym wykryła błąd ... na który ja bym w życiu nie wpadła ... i tak bym siedziała i robiła i robiła ... do usrany śmierci ...

AS: Moja propozycja taka. Najpierw zebrać potrzebny materiał do rozwiązania zadania. 1. Równanie prostej przez 1 punkt 2. Równanie prostej przez 2 punkty 3. Współczynnik kierunkowy prostej 4. Warunek prostopadłości 5. Rozwiązywanie układów równań liniowych 6. Wzór na odległość punktu od prostej. To wszystko spisane na kartce niech leży przed oczami Ułożyć plan rozwiązania

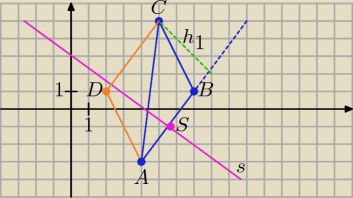
Bogdan: Przedstawiam pełne rozwiązanie. a) Równanie prostej zawierającej punkty A(4, −3), B(7, 1):

	−3 − 1		4
Współczynnik kierunkowy tej prostej: a1 =		=		,
	4 − 7		3

	4		4		25
Równanie kierunkowe tej prostej: y − 1 =		(x − 7) ⇒ y =		x −
	3		3		3

Równanie ogólne tej prostej: 4x − 3y − 25 = 0 Punkt C = (5, 5).

	|4*5 − 3*5 − 25|
Wysokość trójkąta h1 =		= 4
	√42 + 32

b)

	4 + 7		−3 + 1		11
S − środek odcinka AB, S = (		,		) = (		, −1)
	2		2		2

Równanie kierunkowe prostej s: y = a₂x + b₂, która jest symetralną boku AB i która jest

	4		25
prostopadła do prostej y =		x −		oraz przechodzi przez punkt S.
	3		3

	3
Z warunku prostopadłości prostych otrzymujemy a2 = −
	4

	3		11
Prosta s: y + 1 = −		(x −		)
	4		2

	11		25
y = −		x +
	2		8

c) Wyznaczamy punkt D = (x_D, y_D). Wektory BC i AD są równe, stąd: x_D − 4 = 5 − 7 ⇒ x_D = 2 y_D + 3 = 5 − 1 ⇒ y_D = 1 D = (2, 1)

Eta:

Charlize: A wiecie co wam powiem, że zrobiłam sama to zadanie tylko tego punktu D nie wyznaczyłam ... i jutro wam napisze jak bo zaraz idę biegać ... A i jutro wam napisze jescze 2 zadania bo nie jestem pewna ale chyba w odpowiedziach są błędy ...

Eta: OK tak trzymaj! pozdrawiam.

AS: Do Charlize. To aż lasu potrzebujesz? A nie wystarczy szyja fajnego chłopaka!

Eta:

Charlize: Hej ludzie może mi ktoś powiedzieć skąd moge ściągnąc ten program do rysowania tych wykresów ... ? Bo ten Geonext nie chce mi chodzić ... Ściągnełam go ale jest jakiś błąd ..

Charlize: Kurcze bo nie wiem jak wytłumaczyć jak to zadanie zrobiłam ... Hmm ...

tim: Na forum masz uproszczoną wersję programu do rysowania, widzisz?

tim:

Charlize: chodzi o ten przycisk rysuję ? Jesli tak to dużo bawiuńciania się z tym ...

tim: Tzn, zależy co rysujesz . Możesz także w paincie narysować

tim: Spróbuj opowiedzieć na podstawie rysunku mojego lub Bogdana...

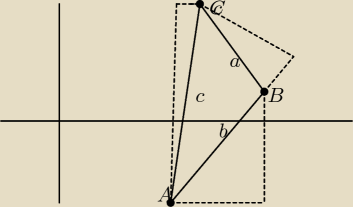
Charlize: Noi tak rysunek nie dokładny, ale mam nadzieje, ze się mniej więcej pokapujecie o co mi biega ... Punkt C jest o jedna kratke za nisko bo zabrakło mi miejsca ... i linia przerywana przy odcinku BC, tam ma być kąt prosty ale coś mi nie wyszło ...

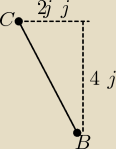
Charlize: A więc zaczne od tego, ze poprzedłużałam sobie boki tymi liniami przerywanymi ... i pokratkach wyliczyłam jaką mają długość ... i tak przy boku "c" dłuższa linia ma kratek 8 i krótsza ma 1 kratke .. i ze wzoru pitagorsa wyliczyłam bok "c" c² = 8² + 1² = √65 Bok b również z tym samym sposobem (linia od punktu A 3jednostki, a linia od punktu B 4j) b² = 3² + 4² = 25 = √25 = 5 Bok a (poprawka na rysnku za pomniałam tego dorysować) a²= 2²+4² = 20 = √20

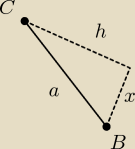
Charlize: A więc mam obliczone boki trójkąta. Żeby obliczyć h zrobiłam taki uklad równań c²= h² + (b+x)² a² = h² + x² c² = h² + b² + 2bx + x² a² = h² + x² / −1 c² = h² + b² + 2bx + x² − a² = − h² − x² po skróceniu zostaje mi c² − a² = b² + 2bx

Charlize: potem podstawiam do wzoru i wyliczm x √65² − √20² = 5² + 2 * 5x 65 − 20 = 25 + 10x 45 = 25 +10x 45− 25 = 10x 20 = 10x x = 2 i teraz podstawiam do wzoru c² = h² + (b +x)² i wyliczam h ... nie chce mi sie już pisać ale z tego wychodzi, ze h=4

Charlize: no to to jest podpunkt a) ... A teraz mam takie pytanie do was ... Po wysokość wziełam z rysunku Bogdana ... i jesli w zadaniu zawsze bede miec polecenie zeby obliczyc wysokośc spuszczona z jakiegos tam punktu na jakis tam odcinek to powinnam przedłużac dany odcinek ... ?

Charlize: b) Najpierw obliczyłam punkt S (5.5; 1) potem zaznaczyłam go na odcinku i narysowałam prostąprostopadłą do odcinka AB Wyznaczyłam wzór odcinka AB 1= 7a + b − 3 = 4a + b / * −1 1 = 7a + b 3 = − 4a − b −−−−−−−−−−−−−−−−−−−−−−−− 4 = 3a a= 4/3 potem podstawiam a do pierwszego i obliczam b b= −8 1/3 całość y= 4/3x − 8 1/3 potem wyznaczam wzór prostej prostopadłej do odcinka AB i teraz jesli się mylę ze wzorem bo takiego nas nuczyli w szkole a₁ * a = − 1 i jeśli podstawie za a 4/3 to po obliczeniach a₁ wychodzi − 3/4 żeby obliczyć b₁ do wzoru y= ax+b podstawiam współrzędne punktu S i a₁ b= 25/8

Charlize: czyli y= −3/4 + 25/8 noi to jest równanie symetralnej A teraz tak w odpowiedziach zostało wspomniane o: "Zapisanie równania rodziny prostych prostopadłych do prostej AB" o co z tym chodzi ? a i może mi ktoś jeszcze to wytłumaczyć ? "Napisanie równania prostej AB" 4x − 3y − 25 = 0 " ← skąd im się to wzieło ? W odp jest zaraz na początku ...

Charlize: No to to by było na tyle jeśli chodzi o podpunkt a i b ... niestety podpunktu c nie zrobiłam ...

123: Co do :"Napisanie równania prostej AB" 4x − 3y − 25 = 0 " ← skąd im się to wzieło ? W odp jest zaraz na początku ... " przeanalizuj podpunkt a w poście Bogdana (3 linijka od dołu) i znajdziesz odp

Charlize: Wyznaczamy punkt D = (x_D, y_D). Wektory BC i AD są równe, stąd: x_D − 4 = 5 − 7 ⇒ x_D = 2 y_D + 3 = 5 − 1 ⇒ y_D = 1 D = (2, 1) Z jakich wzoró to jest liczone ... ?

123: Troche nie mogę się połapac o co chodzi w Twoich postach, ale naucz się tych wzorów co wykorzystuje do obliczenia Eta i Bogdan, one ułatwiają obliczenia.Ty rozwiązujesz na "około",co zabiera czas(tak samo kiedyś robiłem,ale Eta udzieliła mi kilku wskazówek)

Charlize: Właśnie te wzory Ety czy Bogdana mi nie podchodzą jakoś nie moge sie w nich połapać ... lepiej jest mi tak ... Tylko now łaśnie czy na maturze mi to uznają ... o.O ? To moje liczenie ...

Charlize: No nie wiem może ktoś tu jeszcze wpadnie żeby to przeanalizować i sprawdzić ...

Bogdan: Dzień dobry. Jeśli dane są 2 punkty: A=(x_A, y_A), B=(x_B, y_B), to najwygodniej jest napisać równanie prostej przechodzącej przez te punkty korzystając z wzoru: y − y_A = a_AB*(x − x_A) lub y − y_B = a_AB*(x − x_B) gdzie a_AB to współczynnik kierunkowy tej prostej:

	yA − yB		yB − yA
aAB =		lub aAB =
	xA − xB		xB − xA

W tym zadaniu: A=(4, −3), B=(7, 1)

	−3 − 1		−4		4
Wyznaczamy najpierw współczynnik kierunkowy aAB =		=		=
	4 − 7		−3		3

	4		4		28
Teraz tworzymy równanie prostej: y − 1 =		(x − 7) ⇒ y =		x −		+ 1.
	3		3		3

	4		25
Ostatecznie otrzymujemy: y =		x −		.
	3		3

To jest postać kierunkowa prostej. Do wyznaczenia długości wysokości trójkąta opuszczonej z punktu C=(5, 5) można skorzystać z wzoru na odległość d punktu P(x₀, y₀) od prostej opisanej wzorem ogólnym: Ax + By + C = 0:

	|A*x0 + B*y0 + C|
d =
	√A2 + B2

	4		25
W naszym zadaniu przekształcamy równanie kierunkowe prostej: y =		x −
	3		3

do postaci ogólnej: 4x − 3y − 25 = 0 (A=4, B = −3, C = −25, x₀ = 5, y₀ = 5)

	|4*5 − 3*5 − 25|		20
h =		=		= 4.
	√42 + 32		5

Bogdan: Charlize, nie ma znaczenia, czy jakiś wzór "podchodzi" Ci, czy nie, jeśli jesteś uczennicą szkoły średniej i taki wzór znajduje się w materiale nauczania, to masz obowiązek znać go i umieć stosować, szczególnie powinnaś umieć wykazać się umiejętnością jego zastosowania podczas matury (bo czymże jest matura?, jak nie sprawdzianem wiedzy objętej programem nauczania w szkole średniej).

Charlize: Bogdan a te moje obliczenia są złe ... ? Chodzi o to, ze je te wasze wzory widze pierwszy raz na oczy ... i nigdy ich niestosowałam w zadaniach ...

Charlize: Co do systemu nauczania w mojej szkole nie będę się wypowiadać ... bo aż szkoda słów ...

Charlize: Mam tu jeszcze jedno zadanie ... W ostrosłupie prawidłowym trójkątnym krawędź boczna jest nachylona do płaszczyzny podstawy po kątem α= 60 stopni, a promień okręgu wpisanego w podstawę jest równy 3√3. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa noi ja to zadania rozwiązałam ale w odpowiedziach jest ciut inaczej ...

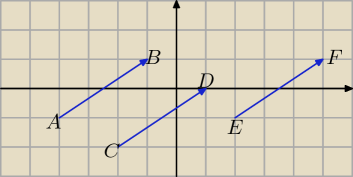
Bogdan: Przypominam podstawowe wiadomości o wektorach: Przykład: → A=(−4, −1), B=(−1, 1), AB = [−1 − (−4), 1 − (−1)] = [3, 2], → C=(−2, −2), D=(1, 0), CD = [1 − (−2), 0 − (−2)] = [3, 2], → E=(2, −1), F=(5, 1), EF = [5 − 2, 1 − (−1)] = [3, 2]. Wektory AB, CD, EF są równe, bo równe są ich współrzędne. W tym zadaniu: → B=(7, 1), C=(5, 5), BC = [5 − 7, 5 − 1] = [−2, 4] → A=(4, −3), D=(x_D, y_D), AD = [x_D − 4, y_D + 3] Wyznaczamy punkt D = (x_D, y_D). Wektory BC i AD są równe, stąd: x_D − 4 = −2 ⇒ x_D = 2 y_D + 3 = 4 ⇒ y_D = 1

Bogdan: Twoje obliczenia są bardzo żmudne, czasochłonne i mówiąc bez owijania w bawełnę, trochę nie przystające do maturzysty. Podczas egzaminu maturalnego czas jest na wagę złota i nie można sobie pozwolić na jego marnotrawienie na czasochłonne rachunki. Jestem zdziwiony, że widzisz po raz pierwszy pewne wzory. Przejrzyj swoje podręczniki od klasy pierwszej do klasy maturalnej, na pewno tam są. Maturzysta winien również znać tablice matematyczne, a także arkusze maturalne z wzorami.

Charlize: To ciekawe tylko my nigdy nie uczyliśmy się o wektorach ... x_X Wektory były na fizyce ... ale już tego nie pamiętam ... Wyznaczamy punkt D = (xD, yD). Wektory BC i AD są równe, stąd: xD − 4 = −2 ⇒ xD = 2 yD + 3 = 4 ⇒ yD = 1 skąd wzieło ci się −2 ... ?

Bogdan: W tym portalu, obok (po lewej stronie tego okna) masz całą wiedzę podzieloną na działy. Jest tu również dużo rozwiązanych przykładów. Zachęcam do przestudiowania tego materiału.

Bogdan: → bo BC = [−2, 4]

Bogdan: → → AD = BC ⇒ [x_D − 4, y_D + 3] = [−2, 4]

Charlize: Niestety nie mam już tych podręczników ... mam tylko do 3 klasy ale tam tez nic nie ma o wektorach ... ... Tylko, że mi dużo czasu wyliczenie tego nie zajęło ... No to się skatowałam i zostaje mi dalej sznur i do lasu ...

Bogdan: Kliknij w to i18 , znajdziesz tu informacje o wektorach.

Bogdan: No to postąpiłaś nieroztropnie pozbywając się podręczników, które zawierają materiał potrzebny do zdania matury.

Bogdan: Polecam 1249

Charlize: Nie dobra ide stąd ... bo kat coraz większy ... my w życiu nic o wektorach nie braliśmy, a jak braliśmy to mnie w szkole mogło nie być ... Cóż bede robić po swojemu bo uczenie sie nowycyh wzorów których nie kapuje i nie wiem jak się używa nie ma sensu ... zwłaszcza teraz ...

Charlize: A na temat mojej matury nie będe się rozwarstwiać bo dużo pisania o tym no cóż .. trudno się mówi człowiek popełnia błędy .. i z aniektóy musi słono płacić tak jak w moim przypadku ...

Charlize: Bogdan co ty mi tu poziom rozszerzony pokazujesz ... ? ja podstawowego do końca nie mam przerobionego ...

Bogdan:

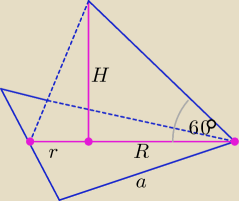
	1
r − długość promienia okręgu wpisanego w trójkąt równoboczny, r =		a√3
	6

a − długość boku trójkąta równobocznego,

	1
r = 3√3 ⇒		a√3 = 3√3 ⇒ a = 18
	6

	1
R − długość promienia okręgu opisanego na trójkącie prostokątnym, R =		a√3,
	3

	1
R =		*18*√3 = 6√3
	3

H − długość wysokości ostrosłupa. Z trójkąta prostokątnego o przyprostokątnych H i R wyznaczamy H:

H
	= tg60o ⇒ H = 6√3*√3 = 36
R

Myślę, że dalej już sobie poradzisz. Powodzenia.

Bogdan: Nie wiem przecież, co masz przerobione i na jakim poziomie.

Bogdan: Przepraszam, błąd rachunkowy, powinno być H = 6√3*√3 = 18

Charlize: Ale tak czy siak ... zdaje na podstawie .. Dobra nie kłócimy się bo nie o to chodzi ... A ten trójkąt ? to co ma ilustrować ... ?

123: rozwiązanie zadania z ostrosłupem , które podałaś.

Charlize: kurde zapomniałam o tym zadaniu z ostorsłupem ... Hm ... Bogdan ja obliczyłam to zadanie tylko z odpowiedziami mi sie nie dokonca zgadza ...

Kuba: Charlize to zdajesz podstawe czy rozszerzenie?

Kuba: aaaa na podstawie ominołem wczesniej ten wątek

Kubuś: raczej ominąłem

Kuba: no tak

ola: podstawe a ty?ΩΔπδγβα