| ∥ | ∥ | ||
< arg(z − i) ≤ | |||
| 6 | 3 |
 .
.
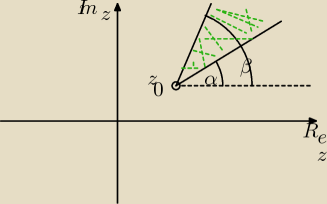 Jak masz coś takiego
α < arg(z−z0) < β
to ogólnie to będzie jak na rysunku.
Jak masz coś takiego
α < arg(z−z0) < β
to ogólnie to będzie jak na rysunku.
| π | π | |||
W zadaniu z0 = i, α = | , β = | |||
| 6 | 3 |
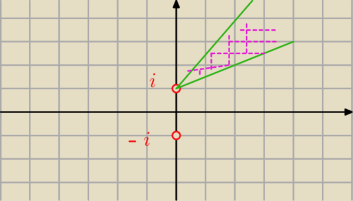 z0 to punkt (0,1) bo z0 = i czyli z0 = 0 + i1
a jak by w nawiasie było z + i to będzie punkt (0, −1)
z0 to punkt (0,1) bo z0 = i czyli z0 = 0 + i1
a jak by w nawiasie było z + i to będzie punkt (0, −1)
 .
Jeśli ogarniasz zespolone, zajrzyj proszę jeszcze tutaj https://matematykaszkolna.pl/forum/181919.html
.
Jeśli ogarniasz zespolone, zajrzyj proszę jeszcze tutaj https://matematykaszkolna.pl/forum/181919.html
 Ja bym to zrobił tak:
|z2 + 2iz −1| < 9
|(z+ i)2| < 9
|(z+ i)| |(z+ i)| < 9
|z + i |2 < 9
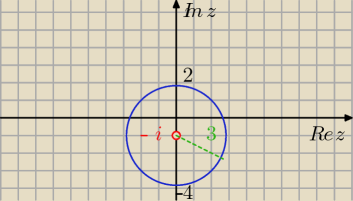
|z+ i| < 3
To będzie wnętrze koła (bez okręgu) o promieniu r = 3 i środku w punkcie z0 = − i.
=======================================================
Interpretacja geometryczna różnicy modułu liczb zespolonych:
|z − z0| < r
=======================================================
Własności modułu liczby zespolonej
|z1 * z2| = |z1 * |z2|
=======================================================
Ja bym to zrobił tak:
|z2 + 2iz −1| < 9
|(z+ i)2| < 9
|(z+ i)| |(z+ i)| < 9
|z + i |2 < 9
|z+ i| < 3
To będzie wnętrze koła (bez okręgu) o promieniu r = 3 i środku w punkcie z0 = − i.
=======================================================
Interpretacja geometryczna różnicy modułu liczb zespolonych:
|z − z0| < r
=======================================================
Własności modułu liczby zespolonej
|z1 * z2| = |z1 * |z2|
=======================================================