funkcja kwadratowa pomocy ! Ola: Mam do Was bardzo wielka prozbe od tego zalezy czy zdam a ja kompletnie tego nie rozumiem mam tutaj 9 zadan fajnie by bylo gdybym miala wszystkie zrobione wiec bardzo was prosze o pomoc 1. parabola, ktora jest wykresem funkcji y=2 (x+1)²+4, ma wierzcholek o wspolrzednych?

	3		1		1
2. wzor w postaci kanonicznej funkcji y=		x2 +		x −		to ?
	4		2		4

3.funkcja kwadratowa, ktorej wykres przechodzi przez punkty (0,−2), (1,−5), (−2,−14), ma wzor ? 4.funkcja okreslona wzorem y= −x² − x + k ma jedno miejsce zerowe dla ? 5.funkcja kwadratowa o miejscach zerowych −2 i 5, ktorej wykres przechodzi przez punkt (1,24), ma wzor ? 6.oblicz wspolrzedne punktow przeciecia wykresow funkcji y= x² − 4x − 3 i y= −x + 1

	3
7. dana jest funkcja kwadratowa y= x2 − x −
	4

a) oblicz wspolrzedne wierzcholka paraboli, ktora jest wykresem tej funkcji b) oblicz miejsca zerowe tej funkcji c) narysuj wykres tej funkcji d) zbadaj monotonicznosc tej funkcji 8. rozwiaz nierownosci:

	3		9
a) −2 x2 > 32 b) −		x2 +		x ≤ 0 c) −2 x2 + 10x − 8 > 0
	5		5

9.drut o dlugosci 100cm chcemy wygiac w prostokatna ramke. oblicz jakie wymiary powinna miec ta ramka, aby prostokat, ktory ogranicza, mial najwieksze pole. Z góry bardzo dziekuje

tim: 1. 79 2. 69 3. 1393 4. Na podstawie wykresów 79 zobacz, kiedy funkcja kwadratowa ma JEDNO miejsce zerowe. 5. 1392 6. Układasz układ równań tych dwóch prostych. 7. Tam poszukać wystarczy.. 8. 1451 9. 1395

Ola: kurcze fajnie by bylo gdyby byly napisane obliczenia bo inaczej mi nie zaliczy ja wogole nie rozumiem funkcji

tim: Tam jest wszystko wyjaśnione. Naprawdę. Zobacz.

tim: Są wzory i przykłady. Podstawiasz dane, albo robisz jak tam.

Ola: tylko ze twoje odp nie pasuja mi tutaj na kartce bo ja mam podane i trzeba wybrac jedna z nich

Ola: ja juz to wszystko patrzalam i tak nie czaje

tim: Ale to nie są oidpowiedzi... Klk=iknij na to

sony: no ale czego nei wiesz ? przecież tim wszystko ci wypisał

tim: Ale no zobacz. Zadanie 1. Masz podane na stronie jak z wzoru obliczyć x_w oraz y_w. Podstawiasz dane ze wzoru i obliczasz.

Ola: wszystkiego

sony: tim za duzo roboty ja bym to zrobił tak 1. rozwiazujesz tak y=a(x−p)²+q 1) y=f(x) 2) y=f(x−p) ... p ||OX,p 3) y=f(x)+q... q||OY,q W=(p,q) tylko że p przepisujesz z odwrotnym znakiem np. współrzędne piszesz sobie na wykresie i robisz parabole y=2(x−3)²−1 1)y=2x² W=(0,0) − rysujesz parabole ramionami do góry bo a>0 o W=(0,0) 2)y=2(x−3)² W=(3,0) rysujesz parabole ramionami do góry bo a>0 o W=(3,0) 3) y=2(x−3)²−1 W=(3,−1) rysujesz parabole ramionami do góry bo a>0 o W=(3,−1) to ode mnie takie wytłumaczenie ale do zadania nie musisz robić tego wszystkiego wystarczy wypisać W=p,q) a reszta to małe wytłumaczenie

sony: chyba że nauczyciel tego wymaga tak jak to jest u mnie =]

adaś =): o co chodzi w 2 zadaniu ? masz zamienić na postać kanoniczną z postaći ogólnej ?

Ola: nie, gdybym wiedziala o co chodzi to bym raczej nie prosila was o pomoc sony przykro mi ale i tak nic z tego nie czaje

Ola: to juz jest w postaci kanonicznej a co trzeba zrobic to nie wiem

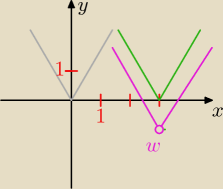
adaś =): narysuj sobie ukł. wsp. i zrób sobie ten przykład u sonego na pewno ci się wszystko wyjaśni tu nie umiem rysowac paraboli ale bym ci to pokazał co i jak to są ala parabole xD nie rysuj takich w zeszycie broń boże xD ale tu masz poklei narysowane wierzchołki w tym przykładzie

adaś =): to może zamienić na postać ogolną ?

Ola: nic takiego nie pisze zeby zamienic ja musze to miec na jutro wiec watpie ze to bede miala

adaś =): w 2 zadaniu to postac ogólna i niewiem o co chodzi z ta dopiską wz. postaci kanonicznej to chyba zamienic

Ola: nie wiem ja nic kompetnie nie rozumiem nawet jak mi napisaliscie a juz nie mam kogo sie zapytac zeby mi zrobil te zadania

adaś =): no to zamieniamy na kanoniczną 1 co robimy obliczamy delte Δ=b⁻4a*c 2 x0 =−b/2a y0=−Δ/4a podstawiamy do wzory y=a(x+p)−q gdzie p=(−b/2a) q=(−Δ/4a) y=a(x+(−b/2a))²−(−Δ/4a) i otrzymujemy postać ogólną

Ola: to chyba razcej nie o to chodzi bo nie mam takiej odp

adaś =): Ola nie przejmuj się szkoda że tak późno napisałaś to jest rozwiązanie do 2 zadania − zamiana postaci ogólnej na kanoniczną

adaś =): a jakąmasz odpowiedz napisz mi odpowiedzi do zadań

Ola: no bo dopiero dzisiaj dostalam te kartki od takiej jednej gdybym zrozumiala cos z tych stron to bym nie chciala pomocy ale juz nawet nie da mi sie tego wytlumaczyc

Ola: do wszystkich

adaś =): no narazie do 2

Ola:

	3		1		1
A. y =		(x +		)2 −
	4		3		3

	3		1		1
B. y =		(x −		)2 −
	4		3		3

	1		1
C. y = (x −		)2 −
	3		3

	1		1
D. y = (x +		)2 +
	3		8

adaś =): no to trzeba podstawić pod te wzory co ci napisałem i wychodzi odpowiedz

Ola: yhym...

adaś =): 1 co robimy obliczamy delte Δ=b²−4a*c 2 x0 =−b/2a y0=−Δ/4a 3 podstawiamy do wzoru postaci kanonicznej postac kanoniczna y=a(x+p)−q gdzie p=(−b/2a) q=(−Δ/4a) y=a[x+(−b/2a)]²−(−Δ/4a) i otrzymujemy postać ogólną i wybieramy odpowiedz

Uczony student: żal ;> 2+2= =/

adaś =): co to =]

Uczony student: Tak to jest =/ w polsce same g3niusze ;>

Uczony student: dwa kwadraty xD

adaś =): miło mi że jesteś zdolny ale nie spamuj tu

Uczony student: A wlasnie przypomnialem sobie mam jutro sprawdzian z brył =/: Oblicz pole całkowite i objetosc graniastroslupa o wym 5cm,5cm.10cm adaś help ~~!

adaś =): napisz nowy temat a w tym niema nic trudnego podstawiasz pod wzór i tyle

Uczony student: A jaki wzór =/

Ola: a jak mam ta delte obliczyc ?

adaś =): Δ=b²−4*a*c z tego wzoru =)

Ola: no ja wiem ze z tego ale jak pamietam ze bylo a b i c ale nie wiem jak to podstawic

Julia: Δ=b²− 4ac

Julia: masz wzór funkcji y=ax²+bx+c

Uczony student: Dobra a mi ktos pomoże

Julia: i podstawiasz co trzeba

adaś =): zad.2 ma postać ogólną czyli taką y=ax²+bx+c rozumiesz ? pod a,b,c podstawiasz te liczby które masz u góry i wpisujesz do wzoru Δ i później do postaci kanonicznej

Julia: No graniastosłup to może być np prostopadłościan, narysuj, oznacz boki i oblicz pole ze wzoru P=2*pole podstawy+pole boczne a objętość V=a*b*c masz wymiary podane

Ola: dobra nie wiecie o co mi chodzi

Ola: ejj uczony student idz z tad

Julia: Wiemy masz wszystko podane, wystarczy obliczyć, poziom 1 liceum...

adaś =): a co ?

Ola: no tak ale ja nie rozumiem funkcji bo mam takiego nauczyciela ktory wogole nie potrafi tlumaczyc i przez to moge nie zdac

Ola: dobra oblicze ta delte i napisze wam jak mi wyszlo

Julia: no to ci tłumaczymy, masz podany wzór funkcji, Ty masz swój, podstaw odpowiednie liczby pod wzór na deltę, oblicz pierwiastki i podstaw do wzoru na postać kanoniczną

Julia: Powiem Ci, ze będzie odp albo A albo B, to już mniej masz do wyboru

adaś =): y=3/4x²+1/2x−1/4

	1		3		1
Δ=		2−4*		*(−		)
	2		4		4

i obliczasz

adaś =): ja nie typowałem odpowiedzi zawsze wyliczam do konca albo strzelam ^^ jak obliczysz Δ to obliczasz x0 i y0 x0 =−b/2a y0=−Δ/4a a następnie podstawiasz pod wzór y=a(x+(−b/2a))2−(−Δ/4a)

Ola:

	3		1		1
y=		x2 +		x −
	4		2		4

Δ= b² − 4ac

	3		1		1
a=		b=		c=
	4		2		4

	1		3		1
Δ=		2 − 4 *		* (−		)
	2		4		4

	1		4		3		1
Δ=		−		*		* (−		)
	4		1		4		4

	1		3
Δ=		− (−		)
	4		4

	1		3
Δ=		+
	4		4

Δ= 1 dobrze ?

adaś =): tak

Ola: i co dalej ?

adaś =): obliczasz x0 i y0 x0 =−b/2a y0=−Δ/4a a następnie podstawiasz pod wzór

	−b		−Δ
y=a[x−(		)]2+(		)
	2a		4a

Ola: to 1 wyszlo mi : x0 = 1/3 y0 = −1/3 dobrze ?

adaś =): x0 = −1/3 y0 = −1/3 chyba tak ma być zapomniałaś o minusie przy x0 ale sprawdź jeszcze raz bo mogę się mylić

Ola: a no tak to teraz mam podstawic za x i y

adaś =): teraz podstawiasz tak jak jest w wzorze u góry nie za x i y tylko za −b/2a i −Δ/4a i już masz postać funkcji kanonicznej

Ola: aha

adaś =):

Ola: tylko nie wiem czy mi dobrze wyjdzie bo to dosc dlugie jest

Ola: o jej ale namieszalam

adaś =): ale podstawiasz obliczone nie wpisujesz tego do obliczania tylko wyniki podstawiasz czyli najkrócej jak sie da

Ola: a ja juz podstawilam xD dlatego mi sie pomieszalo

Ola: to jak to obliczyc bo juz mi sie pomieszalo

adaś =): podstawiasz za a= 3/4 (x− (−1/3))²+(−1/3) i tyle tylko zapisz to poprawnie + i −

Ola: i nic juz wiecej

Ola: wyszlo A

Ola: jejku dziekuje bardzo jeszcze zostalo mi 8 zadan

adaś =): 1 zadanie jest bardzo proste napisałem ci u góry W= (−1,4) wiesz dlaczego ? u góry masz wyjaśnienie z3 juz nie pamiętam duzo rzeczy ale z 4 jest proste z4 obliczasz Δ i jak jest >0 ma 2 miejsca zerowe jak jest Δ=0 ma 1 miejsce zerowe a jak Δ<0 to niema m zerowego

Ola: ja wlasnie tego 1 nie rozumiem

adaś =): z5 tutaj skorzystamy z wzorów zadań na forum https://matematykaszkolna.pl/strona/1392.html tu jest takei samo zadanie tylko odwzorować i wyjdzie ci wynik

adaś =): miejsce zerowe to miejsce przeciecia sie paraboli, prostej z osią X https://matematykaszkolna.pl/strona/79.html

Ola: aha wiem ze jestem trudnym uczniem az dziwie ci sie ze masz stalowe nerwy bo ja bym nie dala rady

Ola: postaram sie to zrobic

adaś =): z7 jest to zadanie związane z każdym zadaniem poklei sobie idziesz i sprawdzasz co i jak bo już to robiłaś a jak czegoś nie wiesz to patrzysz na działfunkcja kwadratowa na forum i tam wszystko pisze z8 a) −2x²>32 −2x²>32/:(−2) x²<−16 i niema nic bo kwadrat żadnej liczby R nie jest liczbą ujemną np. x²=3 = x=√3 a żaden pierwiastek nie jest ujemny zgadza się? w tym zadaniu obliczasz b) ,c) obliczasz Δ − Δ>0 = x1(−b−√Δ/2a), x2(−b+√Δ /2a) , Δ=0 (x0=−b/ 2a), Δ<0 niema miejsc zerowych zezeli Δ>0 rysujesz parabolę przechodząca przez x1 i x2 jezeli a>0 ramiona są do góry jeżeli a<0 to ramiona są na dół jeżeli Δ=0 rysujesz parabole stykającą sie z punktem x0 i to samo co przedtem z ramionami ekstremum masz na forum minimum i maximum wszytsko jest w dziale funkcja kwadratowa a zad. 9 masz tu https://matematykaszkolna.pl/strona/1395.html tylko podkładasz inne liczby ja muszę lecieć uczyć się angola myślę że sobie poradzisz z tymi materiałami na forum i z tym co sama zrobiłaś pozdrawiam

Ola: tak mi wyszlo: y= a ( x − (−2) ) (x − 5) y= a (x + 2) (x − 5) ____________________ 24= a (1 + 2) (1 − 3) 24= a * 3 * (−2) 24= −6a / (−6) −4 = a a= −4 ______________ y= −2 (x + 2) (x − 5) wyszlo C

Ola: ok dziekuje bardzo za pomoc powodzenia z angielskim papa

adaś =): dobrze