Geometria analityczna qwert01: Witam Dany jest odcinek o końcach A(−1, 2) , B(7, −4) a) podaj równanie ogólne prostej AB b) wyznacz równanie symetralnej s odcinka AB c) znajdź na symetralnej s punkt C, którego odległość od odcinka AB wynosi 10. Jaka jest odległość punktu C od punktów A i B? a) i b) zrobiłem ale mam problem z c) Proszę o wytłumaczenie jak to zrobić.

Artur_z_miasta_Neptuna: teoria: https://matematykaszkolna.pl/strona/1249.html jeżeli nie pamiętasz wzoru to: krok1 masz juz wzór symetralnej krok2 wyznaczasz punkt przecięcia się symetralnej z odcinkiem AB krok3 wyznaczasz punkt C tak aby odległość tego punktu od punktu przecięcia się symetralnej z odcinkiem AB wynosiła dokładnie 10

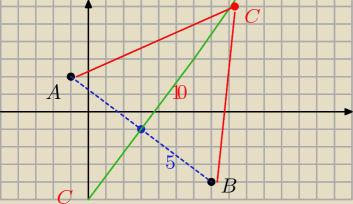
aniabb: to samo w doł C(9;7) C'(−3;−9) CA=CB = √125

qwert01: nadal nie wiem jak wyznaczyć ten punkt C, ze wzoru na odległość punktu od prostej mam dwie niewiadome x i y, więc jak to obliczyć?

Artur_z_miasta_Neptuna: nie masz dwóch niewiadomych masz jedną bo y= ax+b <−−−− wzór symetralnej s więc punkt ma współrzędne (ax+b ; x) <−−− jedna niewiadoma (bo wzór symetralnej podobno masz juz wyznaczony)

aniabb: (x;ax+b)

qwert01: prosta AB: 3x+4y−5=0 symetralna s: −4x+3y+15=0 y=4/3x−5 C(x;ax+b) czyli C(x;4/3x−5) tak powinno być? po podstawieniu wyszedł mi zły wynik, co jest źle? równania prostych sie zgadzają z odpowiedziami

aniabb: środek AB np D(3,−1) https://matematykaszkolna.pl/strona/1750.html i teraz DC=10 więc (x−3)² + (4/3x−5−(−1))² = 10² (x−3)² + (4/3x−4)² = 10² delta....

Mila: a) A(−1, 2) , B(7, −4) równanie prostej AB: y=ax+b (kierunkowe) 2=−a+b −4=7a+b odejmuję stronami; 6=−8a

	3		3		5
a=−		⇒2=		+b⇔b=
	4		4		4

	3		5
y=−		x+		/*4⇔4y=−3x+5⇔
	4		4

3x+4y−5=0 równanie ogólne prostej AB b)Symetralna AB

	−1+7		2+(−4)
s⊥AB i przechodzi przez środek AB; sx=		; sy=
	2		2

S=(3;−1)

	4		4
s: y=		x+b; −1=		*3+b; b=−5
	3		3

	4
s:y=		x−5
	3

	4
c) Punkt C; C∊s⇔C=(x,		x−5)
	3

4   |3x+4( x−5)−5|   3
	=10
√32+42

stąd x=9 lub x=−3 y=.. lub y=..

qwert01: Dzięki, już mi wyszło miałem błąd w obliczeniach.