Planimetria - trójkąt Artur: Witam wszystkich, mam problem z takim zadankiem: Dany jest trójkąt ABC, w którym długości boków są równe: IBCI=4 ICAI=8 IABI=4√7. a) Wyznacz miarę kąta rozwartego w trójkącie ABC oraz oblicz długość wysokości poprowadzonej z wierzchołka tego kąta. b) Oblicz stosunek długości promienia okręgu opisanego na trójkącie ABC do długości promienia okręgu wpisanego w ten trójkąt. Proszę o pomoc

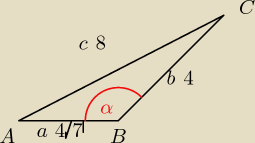
aniabb: c²= a²+b² −2ab*cosα

aniabb: zapomniałam o wysokości na rysunku .. a² +h² = x² b² +h² = (8−x)²

Artur: OK tylko czy kąt rozwarty nie powinien być kątem BCA?

aniabb: https://matematykaszkolna.pl/strona/542.html i https://matematykaszkolna.pl/strona/541.html więc R={c}{2sinα}

abc
	= r(a+b+c)/2
4R

absinα
	= r(a+b+c)/2
2

	absinα
r=
	(a+b+c)

aniabb: ok faktycznie zapomniałam o 4 przed pierwiastkiem zamień a z c i będzie ok

Artur: Spoko dzięki wielkie

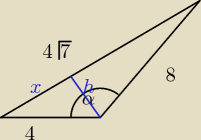
aniabb: 112=16+64−64cosα cosα=−1/2 α=120°

aniabb: i bez rysunku nawet Pitagorasy pomieszałam x²+h²=16 (4√7 − x)² +h² = 64 112 −8√7x+x²+h²=64 112−8√7x+16=64 x=8/√7 h²=16 −64/7 = 48/7 h= √48/7

Artur: Spoko, nie trzeba było ale dziękuję

aniabb:

	4√7		4√7
R=		=
	2*sin120°		√3

r= 16√3 / (12+4√7)

Artur: Heh OK Dzięki