Równania
Tomek: Prosiłbym o pomoc w równaniach, bo nie mam pojęcia jak za nie się zabrać.
Rozwiązać równanie
sin(5x) − sin(3x) = 0
4sin2x − 4|cosx| − 1 = 0
16 lis 09:07
16 lis 09:22
Tomek: Czyli będzie:
2 sin(1) x cos(4) ?
16 lis 09:32
aniabb: 2*sin(2x)*cos(4x)=0
16 lis 09:40
16 lis 09:41
Tomek: Dlaczego 2*sin(2x)*cos(4x)=0 a nie 2*sin(x)*cos(4x)=0 ?
No i co dalej z tym zrobic?
16 lis 09:43
aniabb: ok sin x
dalej to żeby iloczyn równy był zero to przynajmniej 1 musi być 0
liczysz każde oddzielnie
16 lis 09:51
Tomek: sin(2x) = 0
a tutaj w 0 ?
cos (4x) = 0
16 lis 09:54
Bogdan:
Przepraszam, że się wtrącę.
W pierwszym równaniu rozwiązanie jest podane od razu:
sin(5x) = sin(3x)
5x = 3x + k*2π lub 5x = π − 3x + k*2π
2x = k*2π lub 8x = π + k*2π
| | 1 | | 1 | |
x = k*π lub x = |
| π + k* |
| π |
| | 8 | | 4 | |
16 lis 09:56
aniabb: a w drugim i tak zamienimy na kwadratowe z t
a juz myślałam że wszystko pod wzorek
16 lis 09:58
aniabb: sin2x = 1−cos2x
a potem podstaw cosx =t
16 lis 10:03
Tomek: Moglbym poprosic o wyjasnienie skad sie wziela 2 linia u Ciebie Bogdan?
16 lis 10:03
Tomek: *aniabb
A 4 przy sin i cos zniknela?
16 lis 10:05
aniabb:
16 lis 10:06
aniabb: ja ci podałam tylko jak tutaj zamienić sin na cos .. mam wrażenie że podstawić do równania
będziesz umiał sam
16 lis 10:07
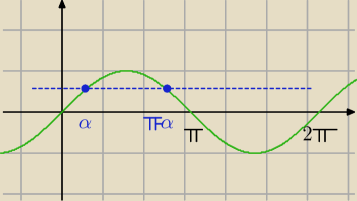
aniabb: a rysunek to do 2 linijki Bogdana .. z sin są dwa rozwiązania (oprócz cykliczności co 2kπ co
widać dalej)
x= α lub x= π − α
16 lis 10:08
Tomek: −4cos2x − 4cos|x| = 3
? Co zrobic z |x| ? Dwa przypadki trzeba rozważyć?
16 lis 10:16
MQ: cos x jest funkcją symetryczną, więc cos x = cos (−x)
Możesz więc pominąć wartość bezwzględną i wziąć samo cos x
16 lis 10:19
Tomek: A mam jeszcze pytanie odnosnie 1 przykladu:
tg(2x) − tg(x) = 0
Ze wzoru:
| sin(2x−x) | | sinx | |
| = |
| I co dalej? |
| cos(2x)*cos(x) | | cos22x | |
16 lis 10:35
Bogdan:
Podaję pełne rozwiązanie drugiego zadania.
4sin
2x − 4|cosx| − 1 = 0, |cosx| ≤ 1
4(1−cos
2x) − 4|cosx| − 1 = 0 ⇒ 4−4cos
2x−4|cosx|−1=0 ⇒ 4|cosx|
2 + 4|cosx| − 3 = 0
Δ = 16 + 48 = 64,
√Δ = 8
| | −4 − 8 | | −12 | |
|cosx| = |
| = |
| < −1, sprzeczność |
| | 8 | | 8 | |
lub
| | −4 + 8 | | 1 | | 1 | | 1 | |
|cosx| = |
| = |
| ⇒ cosx = − |
| lub cosx = |
| |
| | 8 | | 2 | | 2 | | 2 | |
| | π | | π | | π | |
cosx = −cos |
| ⇒ cosx = cos(π − |
| ) lub cosx = |
| |
| | 3 | | 3 | | 3 | |
| | 2 | | 2 | | π | | π | |
x = |
| π + k*2π lub x = − |
| π + k*2π lub x = |
| + k*2π lub x = − |
| |
| | 3 | | 3 | | 3 | | 3 | |
k∊ℂ (ℂ − zbiór liczb całkowitych)
16 lis 10:55
Bogdan:
| | π | | π | | π | | π | |
tg(2x) = tg(x), 2x ≠ |
| + k*π ⇒ x ≠ |
| + k* |
| i x ≠ |
| + k*π |
| | 2 | | 4 | | 2 | | 2 | |
2x = x + k*π ⇒ x = k*π
16 lis 11:01