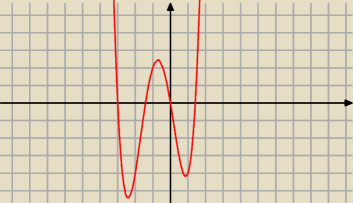
Liczby rzeczywiste4. Mańka: Wykaż, że istnieje liczba całkowita spełniająca nierówności: x⁴+3x³+2x²−6x<0

Kejt: x³(x+3)−2x(x+3)<0 (x³−2x)(x+3)<0 x(x²−2)(x+3)<0 x(x+√2)(x−√2)(x+3)<0 x∊(−3;−√2)∪(0;√2) liczbą całkowitą spełniającą tę nierówność jest 1.

Kejt: oj..walnęłam się

PuRXUTM: Kejt niestety źle popatrz na pierwszą linijkę i treść zadania...

Mańka: czyli to jest dobrze czy zle?

Kejt: źle. chwila..

PuRXUTM: może − http://www.wolframalpha.com/input/?i=x%5E4%2B3x%5E3%2B2x%5E2-6x%3C0

Nienor: x⁴−x³+4x³−4x²+6x²−6x<0 x³(x−1)+4x²(x−1)+6x(x−1)<0 (x³+4x²+6x)(x−1)<0 x(x²+4x+6)(x−1)<0 pierwiastki: x=0 i x=1, bo równanie x²+4x+6 nie ma rozwiązań w R. Hmm o ile znak nie równości nie jest inny, nierówność nie ma rozwiązań w C

Kejt: pff..a ten na łatwiznę od razu idzie ale to chyba jakiś błąd w zadaniu, hm? bo napisali, że jest liczba całkowita spełniająca tę nierówność..

PuRXUTM: Kejt nie właśnie teraz obaliliśmy jakieś ważne twierdzenie i będziemy sławni No nieraz idę na łatwiznę, najczęściej nie ale teraz mi się nie chce tego rozwiązywać jak w Wolframie wszystko jest ładnie pokazane

Kejt: ach..okej

Saizou : a może zamiast −6x ma być +6x

PuRXUTM: no jak na to pierwszy raz popatrzyłem to myślałem że tak jest i że zadanie banalne ale patrze drugi raz i −6

Kejt: bardziej podoba mi się pierwsza wersja

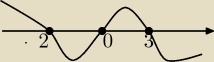
Mańka: nie ma zadnego bledu raczej,tylko to jest rozszerzenie wiem to nie sa latwe sprawy.Ja zrobiłam to w ten sposob alre zapewne jest tu jakis bład w moim rozwiazaniu wiec go poprawcie ok?a mianowicie:x⁴+3x³+2x²−6x<0x(x³+3x²+2x−6)<0x(x²(x+2)+2(x−3))<0x(x²+2)(x+2)(x−3)<0x₁=0 x₂²≠−2 x₃=−2 x₄=3 i na oś, i x∊(−2,0)U(3,+∞)

Mańka: to bd dobrze czy raczej nie?

Kejt: nie.

Mańka: dlaczego? gdzie jest blad?

PuRXUTM: nie tak nie wolno sobie grupować jak Ty zrobiłaś, zobacz co napisał wyżej Nienor

Mańka: oja wiem ze zamiast 3 napisalam 2, zamiast x₃=−2 powinno byc −3

Nienor: Możesz sobie wyciągać przed nawias tylko czynnnik powtarzający się we wszystkich wyrażeniach!

Mańka: no x jest we wszystkim dlatego go wyciagnelam najpierw

Mańka: to nie wiem dlaczego to nie chce wyjsc a moze ktos potrafi pomoc w : https://matematykaszkolna.pl/forum/164073.html https://matematykaszkolna.pl/forum/164074.html https://matematykaszkolna.pl/forum/164079.html https://matematykaszkolna.pl/forum/164080.html

PuRXUTM: jak x! nie Mańka nie o to chodzi musi być np x(x+5) − 6(x+5)=(x+5)(x−6)

Nienor: tak, ale (x+2) już się nie powtarza. Wyrażenie x[x²(x+2)+2(x−3)]≠x(x²+2)(x+2)(x−3)

Mańka: to w takim razie jakie bedzie rozwiazanie tego ? moj swiatopoglad legl w gruzach

Nienor: To co napisałam wyżej. Ja też tak miałam jak się dowiedziałam, że jest rozwiązanie równania x²+1=0

Kejt: a ja wiedziałam stosunkowo wcześnie i irytowałam tym nauczycieli..bo jak przy takim przykładzie mówił:"równanie nie ma rozwiązań" to zawsze go poprawiałam "w liczbach rzeczywistych"

Nienor: Nie no ja tego dowiedziałam się przed liceum czytając o tym w jakimś opowiadaniu, nie o matematyce na dodatek i zaczęłam sprawdzać czy to prawda, no i odpowiedź mnie zdruzgotała U mnie sama zawsze mówiła w zbiorze liczb rzeczywistych.

Mańka: no ale to musi miec jakies rozwiazanie skoro jest wykaż a nie sprawdz

Kejt: Dlatego pisaliśmy, że jest błąd w zadaniu

Karol: nie ma bledu, jesli czegos nie umiecie rozwiazac to odrazu ze jest blad, sympatycznie

Kejt: no to śmiało. rozwiąż

Nienor: Karol ja to rozwiązałam, wykazując, że nie istnieje liczba całkowita spełniająca nierówność

Kejt: ćśś..niech rozwiązuje..ciekawa jestem co mu wyjdzie

	1
może np., że		jest liczbą całkowitą
	2

Karol: juz to kiedys mialem na fakultetach z rozszerzenia z matmy i rozwiazywalismy to, nie pamietam jak to wyszlo i nie mam juz tych notatek wiec sorry nie bd probowal

Nienor: Chwalisz się, czy się żalisz? Zadanie to na fakultetach mogło być trochę inaczej sformułowane (wystarczyłoby, żeby tu była nierówność mięka i już to ma rozwiązania).

Karol: mialem identyczne zadanie bo jest ono z zadan z operonu, pozdro