Oblicz pole i obwód rombu Monika688909: Bardzo proszę o pomoc zadanie jest następujące : Oblicz pole i obwód rombu w którym dłuższa przekątna ma długość 6cm a kąt ostry rombu ma miarę 30stopni .

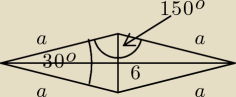
Jakub: W rombie przeciwległe kąty są równe, dlatego jeżeli kąty ostre mają po 30^o to kąty rozwarte muszą mieć po 150^o, aby w sumie dać 360^o (suma kątów w czworokącie) Z twierdzenia kosinusów (zobacz 543) masz 6² = a² + a² −2*a*a cos150^o 36 = 2a² − 2a² cos(90+60^o) 36 = 2a² − 2a² (−sin60^o) 36 = 2a² + 2a²sin60^o 36 = 2a² + 2a^2√3₂ 36 = 2a² + a²√3 36 = a²(2+√3) Dobra dalej już sobie poradzisz z policzeniem "a". Mając bok rombu, już łatwo policzysz pole, chociażby ze wzoru P=a²sinα (zobacz 866)