ciągi:/ HELP ME!!:

	1
Zbadaj monotoniczność ciągu geometrycznego określonego wzorem ogólnym an=3*(		)n
	2

Darek: nie wiem jak czytac, to jest: 3 * ¹₂n czy 3 * {¹₂}ⁿ

Darek: helm me jestes jeszcze

HELP ME!!: 3*(¹₂)ⁿ

HELP ME!!: jestem, jestem

Darek: daj jeszcze chwilke juz koncze xd

Damian:

	1
an = 3 (		)n
	2

	1		1		1
an+1 = 3 (		)n+1 = 3(		)n *
	2		2		2

	1		1		1
an+1 − an = 3(		)n *		− 3 (		)n =
	2		2		2

1
2

ciąg jest malejący...

Damian: Sorry Dareczku nie widziałem ze pomagasz

HELP ME!!: dzięki chłopaki za pomoc

Darek: cza obliczyc iloraz ( q ), czyli wyraz wiekszy podzielic przez mniejszy an=3 * {12}n ja bym zmienil 1/2, aby nie bawic sie w lp. ujemnie 12=2−1, a wiec an=3 * 2−n −−> an=3*2−1*2n = −3 * 2n (to zrobilem pozniej xd wybacz za niekolejnosc, ale w sumie pomyslalem ze tak bedzie lepiej, jak zaczalem dzielic wyrazy ciagu ) mniejszy wyraz to: an−1=3* 2−(n−1) an−1=3* 2−n+1 an−1=3* 2n *2 na podstawie xab=xa * xb an−1=6* 2n teraz dziele ten wiekszy przez ten mniejszy, i ... : anan−1= −3*2n6*2n 2n sie skraca, a z powodu ze anan−1=q to q=−12 poniewaz q jest ujemny to ciag jest malejacy

Darek: a ja i tak wstawie moej dzielo mam wieksze xd !

Darek: btw Damian, jesli to jest geo to powinnysmy liczyc q, a nie r ;> odejmowanie wyrazu wiekszego od mniejszego nasytepuje w c. artytmetyycznym a to geo

Darek: kurde teraz to i mnei sie pomylilo xd q−−> jesli q jest ujemnei w ciagu geo, to ciag nei ejst monotoniczny xd bo ciagle zmienia znak jesli q jest dodatki jest monotoniczny jesli dodatni q jest mniejszy od 1 to ciag malejacy a jesli dodatki q jest wiekszy od 1 to iag rosnacy WIEC moim zdaniem ciag nie jest monotoniczny xd

Darek: niech tu ktos wejdzie o oagrnie bo ja wpadlem w chaos

HELP ME!!: w zasadzie to dlaczego Damian mnoży się razy ¹₂?

Darek: bo mial ten moment ze: {¹₂}ⁿ⁺¹= to jest tak jak ¹₂ⁿ * ¹₂¹ czyli w sumie razy ¹₂ i tak wpadlem tu w chaos

HELP ME!!: ja i tak tego nie rozumiem

Damian: racja.. pomysliłem sie miałem podzielic jeden przez drugi... dzieki za poprawde ale zeby ciąg był malejący to wystarczy że q < 1

HELP ME!!: to jak to w końcu powinno być?

Darek: ok juz mi sie wsio wyjasnilo xd ciag geometryczny to taki ciag, gdzie kazdy wyraz jest mnozony przez jakis q i powstaje kolejny np.: a₁=3 q=2 a₂=a₁*q a₂=6 a₃=12 a₄=24 a₅=48 monotonicznosc funkcji (lub ciagu) oznacza, czy funckja (lub ciag) z kazdym kolejnym wyrazem rosnie, czym maleje, znaczy, czy im dalej, tym wiecej przyklad wyzej pokazuje ze ciag rosnie, q = 2, jesli q byloby = −2 byloby: a₁=3 a₂=a₁*q a₂=−6 a₃=12 a₄=−24 a₅=48 tutaj, q jest ujemnie, wiec nie mozna okreslic monoticznosci, ciag nie ejst monotoniczny, ciagle sie zmienia xd zwieksza i zmnijesza rozwazmy q=¹₂ na nowym przykladzie xd aby bylo latwiej a₁=100 a₂=a₁*q a₂=50 a₃=25 a₄=12,5 a₅=6,25

Darek: wiec moim zdanbiem, rozwiazanie prawidlowe to te ktore tam jest wyyyyyzej xd gdzie q wyszlo −¹₂, wiec ciag nei ejst monotoniczny xd Eh, matematyka to przedmiot gdzie latwo zrobic blad

HELP ME!!: a mógłbyś napisać jeszcze raz jak to zrobić? U góry jest nałożone jedno na drugie i nie widzę co tam jest napisane?

Darek: a od ktorego momentu ah, ciagi geometryczne sa najgorsze xd

HELP ME!!: teraz dziele ten wiekszy przez ten mniejszy, i ... i dalej się nakłada

Darek: cociaz kurcze mysle se teraz, ze monotonicznosc rowniez zalezy od 1szego wyrazu, majac a₁=−2, to jesli q=2 to ciag rowniez jest malejacy ~~ xd w kazdym badz razie, jesli w tym przykladzie wyszlo, ze q jest ujemne, to smialo mozna twierdzic, ze ciag nie jest monotoniczny xd a jakby byl q dodatnie, to musialbys sprawdzic jakie jest a₁ xd poprzez postawienei we wzor ogolny a_n w miejsce n liczbe 1 xd czyli w tym przypadku: a₁=3*¹₂¹ a₁=³₂ wiec a₁ dodatnie xd wiec jesli q byloby dodatnie mnijesze od 0 to ciag malejacy, a jesli q wieksze to rosnacy xd −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− podsumowanie, monoticznosc ciagu: 1) q<0 −−> ciag nie jest monotoniczny 2) q=0 lub q = 1 −−> ciag staly 3) q >0, za wyjatkiem q=1, ciag jets monotoncizny, ale 2 przypadki a) a₁>0, to ciag rosnacy b) a₁<0, to ciag malejacy xd c geo sa be wybacz ze takie to namieszane teraz xd a zara przepisze Ci to cos

HELP ME!!: dzix

HELP ME!!: dzięx*

Kris_garg: W CG (an) dany jest a3 = 4 i a6 = −1/2 a) wyznacz wzór ogólny : czyli a1 * q² = 4 i a1 * q⁵ =− 1/2 z tego mi wyszło a1 = 16, q= −1/2 wzór ogólny an= 16*(−1/2)ⁿ b) oblicz sumę wszystkich wyrazów CG (an) może ktoś pomóc

Darek: aby nie uywac kresek ulamkowych bede ciskal " // " a_n // a_n−1= −3 * 2ⁿ // 6 * 2ⁿ 2ⁿ sie skraca, a jest rownowazne z q (ilorazem): przyklad a₁=3 a₂=6 a_n // a_n−1 = 2, q = 2 bo : 6 // 3 = 2 (dziele wyraz wiekszy o 1 przez ten mniejszy o 1) q rowne jest 2 zapisuje q, bo jest krotsze od a_n // a_n−1 wracajac do zadania, q=−¹₂

HELP ME!!: i ciąg jest malejący?

Darek: kris ale nie mozna obliczyc sumy nie wiedzac, ile jest wyrazow musisz miec dane ilu wyrazow, albo ze a₆ jest tym ostatnim −−−−−−−−−−−−− help, no wlasnie nie, ciag nie jest monotoniczny, q jest ujemnie spojrz gdziest am wyzej, poakzalem rozne przyklady jesli q jest ujemne, to ciagle nastepuje zmiana znaku a₁=2, q = −2 a₂= 2* −2 = −4 2₃ = 8 1szy wyraz dodatni, drugi ujemny, 3ci znow dodatki i tak w kolko

Kris_garg: no właśnie tez tak myślałem ale w zadaniu nie ma tego podanego a w odpowiedzi jest ze S = 10 2/3

Darek: no to ja wymiekam

HELP ME!!: Kris to zadanie to nie w tym temacie, a ja w dalszym ciągu tego nie rozumiem skąd to 56 się wzięło Darek odp Krisa to do zadania : oblicz pierwszy wyraz i iloraz ciągu geometrycznego (a_n), wiedząc, że a₂=28 i a₅=3¹₂. Oblicz sumę dziesięciu początkowych wyrazów tego ciągu.

Darek: ale to chyba w innym zadaniu

HELP ME!!: no to już inne zadanie, z którym też mam problem

Darek: czekaj zerken tam xd jzu znalazlem

Mona Lisa: a_n+1 − a_n = 3 * ( ¹₂ )ⁿ⁺¹ − 3 * ( ¹₂ )ⁿ = = 3 * ¹₂ * ( ¹₂ )ⁿ − 3 * ( ¹₂ )ⁿ = − ³₂ * ( ¹₂ )ⁿ < 0 Ciąg jest malejący.

Darek: odejmowanie wyrazow jest w ciagu arytmetycznym help masz jzu te 56 wyjasnione

Mona Lisa: Ciąg a_n (każdy, nie tylko geometryczny) jest rosnący wtedy, gdy a_n+1 − a_n > 0, jest malejący wtedy, gdy a_n+1 − a_n < 0, a kto tego nie wie, ten kiep.

lisek: Kiepem niestety jesteś Ty. Monotoniczność ciągu geometrycznego określa się w ten sposób:

	an+1
		=q. W zależności jakie q wyjdzie (dodatnie, czy ujemne) określamy jaki to
	an

ciąg

Darek: przyklad q=¹₂ a₁=−12 a₂=−6 a₃=−3 a₄=−1,5 a₅=−0,75 a₆=−0,375 a₂−a₁=−6 − (−12) = −6+12=6 a₂−a₁>0, jednak nie wydaje m isie aby 6 bylo wieksze od 12 moze sie nei znam

HELP ME!!: kurde...to ja już nie wiem jak to zadanie powinno być. Małe zamieszanie tu powstało

Darek: help nie pzrejmuj sie tym co napisane zostalo przez mona lise lisek jak tu jestes, jak uwazasz, jesli q wychdozi −¹₂ mozna powiwdziecm ze ciag nie jest monotoniczny bo moim zdaniem tak xd

Mona Lisa: lisku − jak nie znasz definicji monotoniczności ciągu, to się nie odzywaj. Polecam google, czy jakiś podręcznik.

Mona Lisa: Zajrzyj lisku tu 263

Darek: a nei krude, kurde przyznaje sie do bledu poddaje sie

lisek: wtedy jest malejący

Mona Lisa: Funkcja f(x) = 3*(¹₂)^x jest funkcją wykładniczą, rosnącą? czy malejącą?

Damian: q < 0 ciąg nie jest ciągiem monotonicznym q < 1 ciąg malejący q >1 ciąg rosnący q=0 v q=1 − ciąg stały

Mona Lisa: Kiep

HELP ME!!: to dobrze jest to zadanie czy nie? Jaki jest ten ciąg, malejący? Może ktoś zrobić to zadanie jeszcze raz bo już się pogubiłam

lisek: mona zajrzyj tu 279 wylicz ze wzoru q, a w arytmetycznym 264 wyliczysz r w inny sposób od tego czy liczba ta jest dodatnia, ujemna określa się monotoniczność

lisek:

	1
Dla an=3*(		)n
	2

	an+1		1   3*( )n+1   2		1   1   3*( )n*   2   2
q=		=		=		=
	an		1   3*( )n   2		1   3*( )n   2

	1
=		>0
	2

Zatem ciąg jest rosnący

Damian: Mona to co ty napisałaś jest to wykładnicza malejąca... oczywiście a co do kiepa... miałąśmnie na myśli

HELP ME!!: O ludzie....teraz rosnący? To ja już nic nie rozumiem.

Damian: o MATKO BOSKA BEZLITOSNA.... jesli q<1 to ciąg malejący

Damian: lisek masz a₁ = 4

	1
wyliczyłeś q =
	2

policz mi a₂ a₃ i a₄ i powiedz mi jaki to ciąg

lisek: Damian mówisz o monotoniczności funkcji, a tu jest monotoniczność ciągu

Damian: wiec udowodnij mi że q >1 i ciąg jest malejący... i powiedz wszystkim co sie stanie jezeli q <0 wypowiedz sie... zaraz cie sprostuje

lisek: Masz Damian rację: jeśli q∊(0;1) i a₁>0 to wtedy ciąg jest malejący

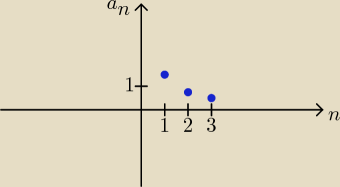
Mona Lisa: n | 1 2 3 4 5 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− a_n = 3 * (¹₂)ⁿ | ³₂ ³₄ ³₈ ³₁₆ ³₃₂ To jest rosnący? czy malejący? Oczywiście malejący, a kto tego nie widzi, ten kiep.

HELP ME!!: To co z moim zadaniem?

Damian: Dziękuje wyjątek stanowi jeżeli a₁ < 0 i q∊ (0;1) to ciąg rośnie a jezeli q >1 to ciąg maleje... HELP rozumiesz

Damian: wiec HELP napisz zadanie jeszcze raz o ktore ci chodzi zrobimy je Miło się posprzeczać wtedy zawsze ale to zawsze ktoś się czegoś nauczy

HELP ME!!: no ok ale nie wiem co z tym zadaniem...już jest tak namieszane, że się pogubiłam

HELP ME!!: Zbadaj monotoniczność ciągu geometrycznego określonego wzorem ogólnym a_n=3*(¹₂)ⁿ

Mona Lisa: Rozwiązałem już to zadanie: a_n+1 − a_n < 0, a więc ciąg jest malejący.

HELP ME!!: ale ja nie potrafię tego rozwiązać

Damian: CHWILA juz pisze co i jak

Damian: wiec PRZECZYTAC TO DO KONCA ZANIM ODPISZECIE

	1
an = 3 * (		)n
	2

żeby zbadać monotoniczność danego ciągu musimy obliczyć wyraz następny tego ciągu czyli a_n+1

	1		1		1
an+1 = 3* (		)n+1 = 3* (		)n *
	2		2		2

nie mamy powiedziane czy jest to ciąg geo czy arytmo wiec liczymy tak

	1		1		1		1
an+1 − an = 3* (		)n *		+ 3 * (		)n =
	2		2		2		2

Wyliczyliśmy różnicę miedzy dwoma wyrazami ciągu teraz nie możemy tego traktować jako geometryczny lub arytmetyczny a₊₁ − a_n > 0 − jesli to prawda to ciąg jest rosnący jesli fałsz to ciąg jest malejący lub stały

1
	> 0 wiec ciąg jst rosnący...
2

kilka tu osob miało rację ale żadna nie miała jej do końca... sam tez się pomyliłem teraz gdyby był to ciąg geometryczny to policzylibyśmy to tak

	an+1
q =
	an

a₁ >0 a₁ >0 q ∊(0;1) wtedy ciąg malejący lub q >1 ciąg rośnie a₁<0 a₁ <0 q ∊(0;1) i ciąg rośnie q>1 ciąg maleje arytmetyczny ciąg : zeby zobaczyc czy ciąg rosnie czy maleje odejmujemy wyraz młodszy od starszego a₊₁ − a_n < 0 jesli prawda − ciąg maleje jesli fałsz ciąg rośnie Mam nadzieje ze to rozjasni umysły wasze

HELP ME!!: ale w zadaniu jest napisane "Zbadaj monotoniczność ciągu geometrycznego określonego wzorem ogólnym"

Damian: skoro pisze geometryczny to liczymy q

	an+1
q =
	an

i popatrz na przedziały powiedz ile ci wyszło a ja powiem ci czy dobrze

HELP ME!!: 3*(¹₂)ⁿ*¹₂ q= −−−−−−−−−−−− 3*(¹₂)ⁿ q= ¹₂ q<0 ciąg malejący

Damian: juz musze leciec rozwiazanie zadania to:

	an+1		1   1   3 * ( )n *   2   2		1
q =		=		=
	an		1   U{3 * ( )n}   2		2

a_n = a₁ * qⁿ⁻¹ q∊(0;1) wiec ciąg jest maljący

Damian: HELP q < 0 NIEPRAWDA błąd masz w zapisie na samym koncu

Damian: będe ok 23 narazicho jak bys mial jeszcze pytania to pisz...

HELP ME!!: ok...dzieki. Miała

alutkach: wiedzac ze (an)jest ciagiem geometrycznym oraz a1=16 a4=−2 wyznacz q i podaj wzor na wyraz ogolny tego ciagu

mas: −6 * 2/3