Rozwiąż Noxer: Rozwiąż równanie: x⁴+4x³−18x²−12x+9=0

sushi_gg6397228: jakies własne propozycje?

Gustlik: x⁴+4x³−18x²−12x+9=0 Schemat Hornera: "Kandydaci" na pierwiastek: +−1, +−3, +−9 1 4 −18 −12 9 1 1 5 −13 −25 −16 −1 1 3 −21 9 0 x=−1 jest pierwiastkiem Mamy: (x+1)(x³+3x²−21x+9)=0 Jeszcze raz Horner; odpada 1, bo wiadomo, że nie jest pierwiastkiem: Liczby, które nie są pierwiastkami − "odpadły" w pierwszym Hornerze możemy w drugim Hornerze odrzucić, bo wiadomo, że nie są one pierwiastkami wielomianu. Ta "dyskwalifikacja kandydatów na pierwiastki" przypomina dyskwalifikację sportowców na zawodach − zawodnik, który odpadł w pierwszej rundzie nie przechodzi do drugiej. U nas taką "zdyskwalifikowaną" liczbą jest 1. 1 3 −21 9 −1 1 2 −23 32 3 1 6 −3 0 x=3 jest pierwiastkiem Mamy: (x+1)(x−3)(x²+6x−3)=0 Δ=48, √Δ=4√3

	−6−4√3
x1=		=−3−2√3
	2

x₂=−3+2√3 Odp: x=−1 v x=3 v x=−3−2√3 v x=−3+2√3

Eta: W(−1)=....

pigor: ... np. tak : szybko znajdujesz, że W{−1)=0 i wtedy dobierasz "w pamięci" w pary współczynniki tak , aby po wyłączeniu wyszło w nawiasach (x+1), np. tak : x⁴+x³ +3x³+3x² −21x²−21x +9x+9= 0 ⇔ x³(x+1) +3x²(x+1) −21x(x+1) +9(x+1)= 0 ⇔ ⇔ x= −1 lub x³+3x²−21x+9= 0 i Q(3)=0 to analogicznie dobierasz w pary np. tak : ⇒ ⇒ x³−3x² +6x²−18x −3x+9= 0 ⇔ [x²(x−3) +6x(x−3) −3(x−3)= 0 ⇔ ⇔ (x−3)(x²+6x−3)= 0 ⇔ x=3 lub x²+6x−3= 0 ⇒ x²+6x+9 −12= 0 ⇔ (x+3)²=12 ⇔ ⇔ |x+3|=2√3 ⇔ x= −3±2√3 odp. x∊{−1,3,−3−2√3, −3+2√3} . ...

Eta: Teraz czekam na długi "komentarz" ......

Piotr: ale bedzie riposta

Gustlik: Pigor, owszem w domu można się tak bawić, aby ćwiczyć mózg. Ale wyobraź sobie, że Noxer będzie pisał maturę rozszerzoną z matmy, a tam czasu na zabawę w grupowanie nie pasujących do siebie współczynników nie ma. Metoda dobra i ciekawa, ale tylko wtedy, gdy mamy dużo czasu. Dlatego ja osobiście zachęcam do zapoznania się ze schematem Hornera, bo w przypadku takich wielomianów jest szybszy od grupowania: https://matematykaszkolna.pl/strona/1401.html , a tutaj moje wyjaśnienie tej metody: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=1401 . Zwłaszcza, że Horner szybko znajduje pierwiastki bez wstawiania za x i potęgowania i jednocześnie dzieli − mamy dwa w jednym − znaleziony pierwiastek i podzielony wielomian. Pozdrawiam

Vizer: Leżę

Eta:

Noxer: A jak znaleźć tych "kandydatów"? −1 jeszcze łatwo sprawdzić, ale co zresztą?

Gustlik: Noxer: "Kandydatów" szuksza z twierdzenie o pierwiastkach całkowitych i wymiernych wielomianu : https://matematykaszkolna.pl/strona/121.html . Potem tych "kandydatów" podstawiasz do schematu Hornera do pierwszej kolumny i 2 wiersza − pod tym pustym zakreskowanym polem, tam gdzie w "moim" przykładzie jest 2 i liczysz schemat Hornera tak długo, aż reszta (liczba w 2 wierszu na końcu tabelki, tam gdzie −7) wyjrdzie 0.

Gustlik: Schemat Hornera − tu masz wyjaśnienie: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=1401 .

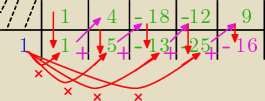
Gustlik: Robisz Hornera tak długo, aż trafisz na pierwiastek, czyli gdy reszta wyjdzie 0. Rozrysuje Ci Twój przykład: 1 4 −18 −12 9 1 1 5 −13 −25 −16 −1 1 3 −21 9 0 Na rysunku zamieściłem tylko pierwszy i drugi wiersz, z tym trzecim myślę, że sobie poradzisz, tylko to przeanalizuj. Możesz zrobić sobie nową tabelkę podstawiając −1 tam, fzie na rysunku jest 1, albo przedłużyć tę tabelkę i zrobić Hornera dla −1, a skreślić drugi wiersz, żeby się nie myliło. Te czerwone x−y pod łukami na rysunku oznaczają mnożenie, a fioletowe strzałki oznaczają dodawanie, zresztą są oznaczone jako +. x=−1 jest pierwiastkiem, bo reszta wchodzi 0. Otrzymujesz: (x−(−1))(x³+3x²−21x+9)=0 (x+1)(x³+3x²−21x+9)=0 I ten wielomian z "zielonego" nawiasu rozkładasz znów Hornerem, otrzymasz funkcję kwadratową i potem z delty.

Bogdan: Szukając kandydatów trafimy na x = −1 oraz x = 3. Możemy więc zapisać równanie w postaci: (x + 1)(x − 3)(x² + ax + b) = 0 Po wymnożeniu i uporządkowaniu otrzymujemy: x⁴ + (a − 2)x³ + (−2a + b − 3)x² + (−3a − 2b)x − 3b = 0 Porównując współczynniki mamy: a − 2 = 4 ⇒ a = 6 oraz −3b = 9 ⇒ b = −3 Wystarczy teraz rozwiązać równanie: x² + 6x − 3 = 0 Można również wykonać dzielenie wielomianów: (x⁴ + 4x³ − 18x² − 12x + 9) : (x² − 2x − 3) = x² + 6x − 3

Noxer: Zrozumiałem. Dziękuje wszystkim