równolełobok Krzychu: Czy w każdym równoległoboku suma kątów leżących na przeciw siebie jest równa 180^o ?

nikt: naprzeciw?

rumpek: 863 tyle w tym temacie (patrz kąty w równoległoboku)

Mila: Suma dwóch sąsiednich jest równa 180.

Krzychu: faktycznie, naprzeciw . Chodzi mi, czy na przykładzie tamtym przedostatnim czy zawsze jest α+β=180^o

rumpek: tak bo to kąty przeciwległe

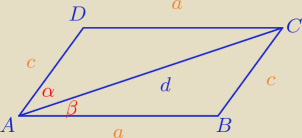
Krzychu: Kąty ostre między przekątną d równoległoboku a jego bokami mają mary α i β. Oblicz obwód i pole tego równoległoboku.

Mila: Rumpek, Krzychu .Kąty przeciwległe w równoległoboku są równe. Suma dwóch sąsiednich kątów w równoległoboku jest równa 180.

Krzychu: to moj rysunek.. Z niego wynika, że 2α+2b=180, czyli a+β=90. To ta figura to jest prostokąt. tak?

rumpek: Mila wiem o co chodzi, tylko nie wiem czemu tyczył się post 14:02 Ja mówiłem o 865

rumpek: Krzychu podaj dokładny temat, z którym masz problem. Bądź wpisz tutaj zadanie

Krzychu: tam wyżej z rysunkiem., w tym zadaniu myślałem że kąty naprzeciwległe mają 180⁰ a tu jednak nie.

rumpek: podaj zadanie

Krzychu: Kąty ostre między przekątną d równoległoboku a jego bokami mają mary α i β. Oblicz obwód i pole tego równoległoboku.

rumpek: I twierdzenie sinusów koniec

Krzychu: ok, a te oznaczenia u mnie w kącie na górze po prawej stornie to w ogóle były ok ?

rumpek: Taki jak rysunek powyżej i jedziemy: 1^o

a		d
	=
sinα		sin(180o − (α + β))

a		d
	=
sinα		sin(α + β)

asin(α + β) = dsinα

	dsinα
a =
	sin(α + β)

rumpek: 2^o

c		d
	=
sinβ		sin(180o − (α + β))

c		d
	=
sinβ		sin(α + β)

csin(α + β) = dsinβ

	dsinβ
c =
	sin(α + β)

3^o L = 2 * c + 2 * a

	2dsinβα		2dsinα		2dsinα + 2dsinβ
L =		+		=		=
	sin(α + β)		sin(α + β)		sin(α + β)

	2d(sinα + sinβ)
=
	sin(α + β)

Pole sam już zrobisz

Mila: Rumpek, wszystko już się zgadza.

rumpek:

Krzychu: a może być z tw. sinusów: a²=d²+c²−2dc cosα c²=d²+a²−2ac cosβ czyli: a=√d²+c²−2dc cosα c=√d²+a²−2ac cosβ Ob=2(√d²+c²−2dc cosα+√d²+a²−2ac cosβ) ?

rumpek: WTF to jest twierdzenie cosinusów Zauważ, że masz 2 niewiadome w swoim rozwiązaniu, więc źle

rumpek: wulgaryzmów na forum się nie używa

nikt: jako dżentelmen wysokiej klasy nie mogę pozwolić aby takie słownictwo było używane na forum Wpis został osunięty Z poważaniem nikt

rumpek: poprzedni login był ciekawszy

nikt: ale miał zbyt wielkie plany i idee Zmieniłem na troszkę bardziej przyziemny

rumpek:

nikt: Ciekawe czy w ogóle ktoś pamięta rozwinięcie starego nicku