CD zadań
Saizou : to może" zadanie na śniadanie";>
29 lip 11:38
rumpek:
1/ Przekątna trapezu równoramiennego tworzy z dłuższą podstawą kąt 2α , a z ramieniem kąt
α Udowodnij, iż stosunek pól trójkątów, powstałych przez podzielnie tą przekątną, jest równy
Takie łatwe na początek
29 lip 11:47
polon: a czy jak mam trapez ABCD i ta przekątna idzie AC to można powiedzieć, że w Wierzchołku A
trójkąta mniejszego jest kąt α a w wierzchołku C trójkąta mniejszego też jest α ?
29 lip 12:00
Saizou :
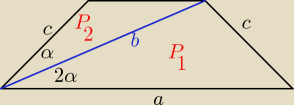
to z tw. cosinusów mamy, że
c
2=a
2+b
2−2ab*cos2α
c=
√a2+b2−2ab*cos2α
zatem
P
1=ab*sin2α
P
2=
√(a2+b2−2ab*cos2α)*b*sinα
dochodzę to tego momentu i nie wiem co dalej
29 lip 12:11
rumpek: 
29 lip 12:13
Jack:
dodaj kąty w trójkącie: podstawa dolna, ramię, przekątna. Dostaniesz kąt w P1 między przekątną
a ramieniem: 180−5α. Walcz!
29 lip 12:14
rumpek:
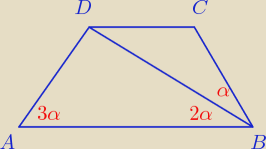
Skoro trapez równoramienny zatem: |∡A| = |∡B|. Dalej powinno pójść banalnie
29 lip 12:14
rumpek: Run Forrest, run
29 lip 12:17
Jack:
dobry rysunek i po zadaniu
29 lip 12:18
polon: faktycznie banał
.
29 lip 12:18
Saizou : P
abd=sin(180−5α)d*c
P
bcd=sinαdc
| sin(180−5α)dc | | sin(180−5α) | |
| = |
| |
| sinαdc | | sinα | |
29 lip 12:29
29 lip 12:30
Jack:
no i ze wzorów red. sin (π−β)=sinβ...
29 lip 12:31
rumpek:
29 lip 12:31
Jack:
rumpek, dajesz kolejne
29 lip 12:31
rumpek: level up
?
29 lip 12:32
Saizou : nie
29 lip 12:35
rumpek:
2 \ Prosta przechodząca przez środek jednego z boków trójkąta równobocznego i tworząca
z tym bokiem kąt ostry α dzieli ten trójkąt na czworokąt i trójkąt. Stosunek pola czworokąta
do pola trójkąta jest równy 5:3. Oblicz tangens kąta α.
29 lip 12:36
Saizou : no nic na razie nie wymyślę, będę się męczyć potem bo teraz idę na obiad
29 lip 13:12
rumpek: ok
29 lip 13:13
Mila: Saizou na obiad, a Rumpek na randkę. Pomagać będzie wcześniejsza generacja.
29 lip 16:15
pigor: ....
właśnie masz rację
Mila , no i mnie wychodzi
tgα = 35√3 
29 lip 16:24
Mila: Witaj Pigor !
29 lip 16:34
rumpek: odpowiedź to: tgα = 3
√3
29 lip 17:22
Mila: Pigor mam wynik bez tej 5 w mianowniku.
29 lip 17:25
rumpek: 
dla
Mili
29 lip 17:27
Mila: Dzięki, Rumpek, Pigor licz jeszcze raz. I czekamy na Saizou.
29 lip 17:29
rumpek: zadanie może się tylko wydawać trudne na początku [jak nie zrobimy rysunku] potem idzie gładko
29 lip 17:32
nikt: nawet mi wyszło xD
29 lip 17:42
Mila: ICSP − nawet chyba już w zeszłym roku?
29 lip 17:45
nikt: nie robiłem tego zadania wcześniej
29 lip 17:47
Saizou :
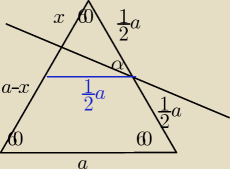
zatem pole czworokąta=5p, a trójkąta 3p
korzystam z wzoru na pole trójkąta równobocznego
zatem
| 3a2√3 | | 1 | | 1 | | √3 | |
| = |
| * |
| a*x* |
|
|
| 32 | | 2 | | 2 | | 2 | |
| 3a2√3 | | ax√3 | | 3a | |
| = |
| →x= |
|
|
| 32 | | 8 | | 4 | |
| | 24 | |
20a2√3=480a→a= |
| →a=8√3
|
| | √3 | |
i dalej nie mam pomysłu
29 lip 18:13
Saizou :
zatem pole czworokąta=5p, a trójkąta 3p
korzystam z wzoru na pole trójkąta równobocznego
zatem
| 3a2√3 | | 1 | | 1 | | √3 | |
| = |
| * |
| a*x* |
|
|
| 32 | | 2 | | 2 | | 2 | |
| 3a2√3 | | ax√3 | | 3a | |
| = |
| →x= |
|
|
| 32 | | 8 | | 4 | |
| | 24 | |
20a2√3=480a→a= |
| →a=8√3
|
| | √3 | |
i dalej nie mam pomysłu
29 lip 18:13
nikt: wiesz ze jeżeli w dowolnym trójkącie masz podane dwa boki oraz chociaż jeden kąt możesz
obliczyć wszystkie kąty oraz wszystkie boki w tym trójkącie ?
29 lip 18:23
Saizou : nie, a przydało by się
29 lip 18:24
nikt: to w takim razie zajmij się trójkątem w którym masz kąt α
Licz wszystko co możesz. Może coś się przyda
29 lip 18:26
Mila: | | 3 | |
x= |
| a − to jest dobrze. |
| | 4 | |
Popraw rysunek ( aby x=3/4a) i narysuj h w Δ z kątem α.
dalej poradzisz sobie.
29 lip 18:34
nikt: Saizou jak chcesz mogę ci dać zadanie z geometrii elementarnej
Oczywiście jeśli jeszcze ci się to nie przejadło
29 lip 18:35
Saizou : a można tak np. z tw. cosinusów wyliczyć z
| | 1 | | 1 | |
a następnie x2=z2+( |
| )2−2x* |
| *cosα |
| | 2 | | 2 | |
29 lip 18:42
nikt: a co chcesz z tego twierdzenia liczyć najpierw?
29 lip 18:47
Saizou :
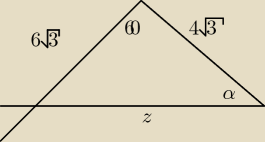
najpierw wyliczyć 'z' a później
(6
√3)
2=z
2+(a
√3)
2−2z*4
√3*cosα
29 lip 18:51
nikt: może być.
29 lip 18:54
nikt: i licz używając zmiennej a
Bez konkretnych liczb.
29 lip 18:55
Saizou : a dlaczego
29 lip 18:59
nikt: ponieważ kiedy a będzie bardzo duże możesz się łatwo zgubić w obliczeniach.
Drugą sprawą jest fakt iż dokonałeś dodatkowych obliczeń aby policzyć a − im więcej obliczeń
tym większa szansa że masz gdzieś błąd.
Łatwiej będzie wstawić na końcu a do gotowego wzorku.
29 lip 19:02
Saizou :
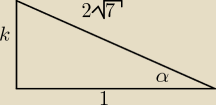
x
2=(6
√3)
2+(4
√3)
2−2*6
√3*4
√3*cos60
x
2=84
x=2
√21
(6
√3)
2=(2
√21)
2+(4
√3)
2−2*4
√3*2
√21*cosα
k
2+1
2=(2
√7)
2
k
2=27
k=
√27=3
√3
29 lip 19:03
nikt:
29 lip 19:07
Saizou : nikt to wrzuć to zadanie
29 lip 19:08
nikt: W trójkącie ABC dane są : |BC| = a, |AC| = b i ∡ACB = 120o.
Oblicz długość dwusiecznej CD
29 lip 19:09
Eta:
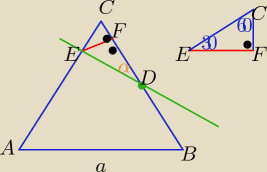
Można też tak:
| | P(ABDE) | | 5 | |
Z warunku zadania ,że |
| = |
| |
| | P(DEC) | | 3 | |
| | 3 | | 1 | | a | | a2√3 | |
wynika,że P(ΔEDC)= |
| P(ΔABC) ⇒ |
| * |
| *|EF|= |
| |
| | 8 | | 2 | | 2 | | 4 | |
Z trójkąta EFC o kątach 30, 60,90 ( lub z f. trygonometrycznych)
| | 3 | | a | | 3 | | 1 | |
otrzymujemy,że |CF|= |
| a , i |FD|= |
| = |
| a= |
| a |
| | 8 | | 2 | | 8 | | 8 | |
| | |EF| | |
zatem z trójkąta EDF: tgα= |
| = 3√3 |
| | |FD| | |
Powodzenia
29 lip 19:26
Saizou :
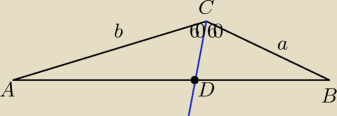
CD=x dla wygody
| | 1 | | 1 | | 1 | |
PABC= |
| *ab*sin120= |
| ax*sin60+ |
| bx*sin60
|
| | 2 | | 2 | | 2 | |
| 1 | | √3 | | 1 | | √3 | | 1 | | √3 | |
| ab* |
| = |
| ax* |
| + |
| bx* |
|
|
| 2 | | 2 | | 2 | | 2 | | 2 | | 2 | |
29 lip 19:33
29 lip 19:33
Saizou :
29 lip 19:46
Eta:
29 lip 19:50
Eta:
Oglądam
tenis
29 lip 19:50
Saizou : a kto gra?
Eto będziesz jak Jadwiga Jędrzejowska albo Agnieszka Radwańska
29 lip 19:52
Eta:
Hehe
.... ja nie gram .... tylko oglądam
29 lip 19:54
Eta:
tenis stołowy
29 lip 19:56
Saizou : kiedyś trzeba zacząć
ale ta Holenderka ma ciut skośne oczy
29 lip 19:58
picia:
TENIS STOŁOWY:
Natalia PARTYKA
QIAN Li
WANG Zeng Yi
Katarzyna GRZYBOWSKA
Kinga STEFAŃSKA
Oto reprezentacja Polski w tenisie stolowym
29 lip 20:00
Saizou : ja wam powiem na razie "sayonara"
29 lip 20:04
Eta:
29 lip 20:05
Eta:
Na dobranoc wrzucę Ci jeszcze parę zadanek
29 lip 20:06
Eta:
@
Saizou łatwe zadanka na "kolację"
zad1/ Wykaż,że ostatnią cyfrą liczby: 5n
2+5n , dla n€N jest
0
| | x2y+3xy2−xy | |
zad2/Wiedząc,że |
| = 12 |
| | 4z | |
Oblicz wartość:
zad3/ Wiedząc ,że f(2x−4)= x+2
Rozwiąż nierówność f(x+1)≤0
zad4/ Wyznacz wielomian W(x) wiedząc,że W(x−1)= x
3+3x+1
zad5/Przekątne trapezu ABCD , gdzie: AB II CD przecinają się w punkcie
P.
Prosta równoległa do podstaw przecina ramiona trapezu w punktach
K i
L
Wykaż,że : |KP|= |LP|
29 lip 20:48
nikt: Eta moge jedno z tych 5
29 lip 21:08
Eta:
29 lip 21:20
29 lip 21:20
nikt: Już zrobione
29 lip 21:23
Eta:
Nie widzę rozwiązania
29 lip 21:28
nikt: Podałaś odp
Nie ma zabawy
29 lip 21:36
nikt: Chyba
Saizou nie chce tych zadanek
Może jedno podbiorę?
29 lip 23:26
rumpek: może ja drugie
29 lip 23:27
Saizou : 1/
5n2+5n=5n(n+1)
n(n+1) jest to iloczyn liczby parzystej i nieparzystej, który jest zawsze parzysty, a iloczyn
liczby 5 i n(n+1) daje liczbę, której liczba jedności jest równa 0
29 lip 23:29
Mila: Nikt i Rumpek macie ładne zadanko u Mat−a.
Eta i Godzio rozwiązali go w zeszłym roku.
29 lip 23:38
nikt: My tutaj motywowaliśmy kolegę
29 lip 23:39
Mila: Rozumiem strategię.
29 lip 23:40
Saizou : 2/
to z pierwszego równania:
| −xy(1−x−3y) | | 48z | |
| =12→1−x−3y= |
|
|
| 4z | | −xy | |
następnie z drugiego
29 lip 23:46
rumpek: ICSP mam zadanie dla Ciebie
Udowodnij nierówność:
√a2 + 1 +
√b2 + 1 +
√c2 + 1 ≥
√6(a + b + c)
29 lip 23:54
Vax: Nierówność tylko dla
ICSP ? I brakuje chyba jednego założenia, chociażby a+b+c ≥ 0
30 lip 00:04
rumpek: Przepisane oryginalnie
30 lip 00:05
nikt: Już się za nią zabieram
Oczywiście podnoszenie do kwadratu z samego początku mija się z celem?
30 lip 00:06
rumpek: ogólnie rozwiązanie to rysunek + 4 linijki
(tak mija się to z celem)
30 lip 00:06
Vax: No musi być przynajmniej założenie, że a+b+c ≥ 0, żeby pod pierwiastkiem nie było liczby
ujemnej.
30 lip 00:07
rumpek: zażalenia do Uniwerku Warszawskiego
30 lip 00:07
Vax: Ja mam rozwiązanie na 1.5 linijki
30 lip 00:08
Saizou : nie mam pomysłów na obecną chwilę może jakaś malutka podpowiedź
30 lip 00:23
rumpek: na które
30 lip 00:23
Saizou : do zadanie 3 bo jadę od 1 do 5
30 lip 00:24
rumpek:
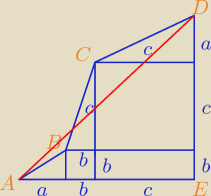
Ustawmy trójkąty prostokątne o przyprostokątnych a i 1, b i 1 oraz c i 1 podobnie [rysunek].
Wtedy
√a2 + 1 +
√b2 + 1 +
√c2 + 1 = AB + BC + CD ≥ AD =
√(a + b + c)2 + 32
Ponadto: (a + b + c)
2 + 3
2 ≥ 6(a + b + c), ponieważ ((a + b + c) − 3)
2 ≥ 0
30 lip 00:32
rumpek: oczywiście przy założeniu, że a,b,c są liczbami dodatnimi
[tak jak pisał
Vax ]
30 lip 00:34
Eta:
zad3/ f(x)= ax+b
f(2x−4)= ..... to f(x) =....
dokończ...........
zad4/ podobnie
30 lip 00:35
nikt: nic nie pisałem xD
30 lip 00:35
rumpek:
30 lip 00:35
nikt: ciekawe co tam Vax wymyślił xD
30 lip 00:36
30 lip 00:36
Eta:
30 lip 00:36
Vax: rumpek, rysunek trochę nie odpowiada temu, co piszesz
(tj w niektórych miejscach
zamiast a,b,c powinna być 1), tą samą literówkę zrobili tutaj:
http://www.deltami.edu.pl/temat/matematyka/geometria/2011/12/31/Najkrotsza_lamana/
Dodatkowo to rozwiązanie wymaga założenia, że a,b,c ≥ 0, a żeby teza zachodziła wystarczy
warunek, że a+b+c ≥ 0, istotnie, wówczas na mocy nierówności Minkowskiego:
√a2+1+
√b2+1+
√c2+1 ≥
√(a+b+c)2+9 ≥
√6(a+b+c)
30 lip 00:37
rumpek: Widzę, też czytujesz tę prasówkę
?
30 lip 00:38
nikt: nierówność Minkowskiego?
Jak ja na to nie wpadłem xD
30 lip 00:40
Vax: Tak, prenumeratę mam nawet
30 lip 00:40
rumpek: me too
30 lip 00:42
Saizou : | | 1 | |
f(2x−4)=a(2x−4)+b=x+2→f(x)= |
| x+4
|
| | 2 | |
0=x+9
x=−9→f(x+1)≤0 gdy x∊(−∞:−9>
30 lip 00:43
Eta:
No i poszło zad3/
30 lip 00:47
Eta:
Miłych snów , dobranoc
30 lip 00:51
Yoyo: Udowodnij że P = NP lub P ≠ NP.
30 lip 00:53
Eta:
Jutro wrzucę następne na "obiad'
30 lip 00:53
Saizou : W(x−1)=x3−3x+1=(x−1)3+3(x−1)2+6(x−1)+5→W(x)=x3+3x2+6x+5
30 lip 00:58
Saizou : a dowód na jutro eeee znaczy dzisiaj zostawiam jak wstanę
Życzę miłych snów i dobranoc wszystkim
do rychłego zobaczyska
30 lip 01:03
pigor: ... 4) Wyznacz wielomian W(x) wiedząc, że
W(x−1)=x
3+3x+1
lub tak :
W(x)=W(x+1−1)= (x+1)
3+3(x+1)+1= x
3+3x
2+3x+1+3x+4=
x3+3x2+6x+5 . ...
30 lip 09:41
Saizou : a Odcinek KL przecina punty P
30 lip 11:00
Saizou :
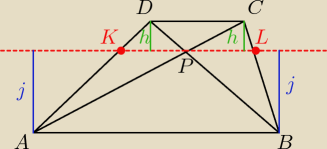
bo jeśli tak to:
P
APD=P
BPC
P
AKP+P
PKD=P
BLP+P
PLC
| 1 | | 1 | | 1 | | 1 | |
| *j*KP+ |
| *h*KP= |
| *j*PL+ |
| *h*PL
|
| 2 | | 2 | | 2 | | 2 | |
| 1 | | 1 | |
| *KP(j+h)= |
| *PL(j+h)
|
| 2 | | 2 | |
KP=PL
cnu.
30 lip 11:20
Saizou : to może zadanie na 2 śniadanie
30 lip 11:41
rumpek:
6 \ Wiedząc, że miara kąta między ramionami trójkąta równoramiennego o polu M jest równa
α. Oblicz promień okręgu wpisanego w ten trójkąt.
30 lip 11:45
Saizou :
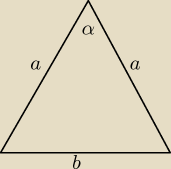
z tw. cosinusów
b
2=a
2+a
2−2*a*a*cosα
b=
√2a2(1−cosα
30 lip 11:53
rumpek: źle
30 lip 11:54
Saizou : a co jest źle?
30 lip 12:02
rumpek: od kiedy to można podać z elementem którego nie ma określonego w poleceniu
?
30 lip 12:03
Saizou : do dzisiaj
ja tworzę nową matematykę
30 lip 12:06
Saizou :
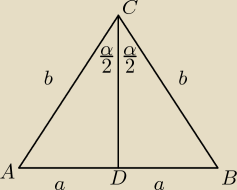
| | ah | |
PABC= |
| zatem PABC=ah=bsinx*bcosx
|
| | 2 | |
| | 1 | | 2P | |
PABC= |
| sin2x*b2→b=√ |
|
|
| | 2 | | sin2x | |
| | 2P | | a+b+c | | a+b+c | |
Korzystam z wzoru r= |
| →P=( |
| )r, zauważam że |
| jest to połowa |
| | a+b+c | | 2 | | 2 | |
obwodu trójkąta, zatem l=połowa obwodu
| | 1 | | 2P | | 2P | | 2P | |
l= |
| (2b+2a)=a+b=√ |
| *sinx+√ |
| =√ |
| (sinx+1)
|
| | 2 | | sin2x | | sin2x | | sin2x | |
wówczas
| | P | | P | | √Psin2x | |
P=lr→r= |
| = |
| = |
| =
|
| | l | | | | √2(sinx+1) | |
30 lip 13:00
30 lip 13:04
Saizou : masz racje zajrzałem bo w ogóle nie miałem pomysłu na to zadanie, ale tylko do momentu:
na wzory na pola
30 lip 13:09
rumpek: to teraz twoje zadanie polega na tym, aby doprowadzić rozwiązanie do końca Twoim pierwszym
sposobem
30 lip 13:10
Saizou : czyli muszę uzależnić "a" od danych z zadaniu
30 lip 13:13
rumpek: bardziej usunąć to a z rozwiązania (oczywiście rozwiązanie sie zmieni) i tak jak robiłeś tw.
cosinusów wynik będzie się troszkę różnił niż na zadania.info
30 lip 13:15
Saizou : możecie mnie oświecić
30 lip 16:55
rumpek:
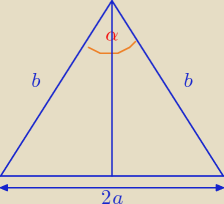
1
o
2M = b
2 * sinα / : sinα
2
o
(2a)
2 = b
2 + b
2 − 2*b*b*cosα
4a
2 = 2b
2 − 2b
2cosα
4a
2 = 2b
2(1 − cosα) / : 2
2a
2 = b
2(1 − cosα) / : 2
| | M(1 − cosα) | |
a2 = |
| , a > 0 |
| | sinα | |
Dalej wiadome
30 lip 17:05
nikt: rumpek ma już przygotowane do wysłania xD
30 lip 17:06
rumpek: co mam
solution?
30 lip 17:08
nikt: pewnie cały zapis jest już w specjalnym pliku i robisz tylko rysunek
Później kopiujesz zapis i gotowe xD
30 lip 17:09
rumpek: nie
przed chwilą rozwiązałem
30 lip 17:10
Saizou : po prostu jestem zły na siebie że na to nie wpadłem
30 lip 17:11
rumpek:
30 lip 17:11
nikt: Ja muszę poprosić
Etę o zadanko które w treści nie będzie miało słowa :
− udowodnij
− wykaż
− pokaż
30 lip 17:13
Saizou : no to uzasadnij
30 lip 17:13
nikt: i żadnego z synonimów tych słów
30 lip 17:14
Saizou : to może jakieś
proste zadanko na deser
30 lip 17:36
rumpek:
2*2 = ...
(...) − odpowiednie uzupełnić
30 lip 17:37
Saizou : 4, ale nie wiem czy nie przypadkiem za dużo
30 lip 17:41
rumpek: udowodnij
30 lip 17:42
Saizou : co mam udowodnić?
30 lip 17:43
rumpek: że 2 razy 2 to 4
30 lip 17:45
Saizou :
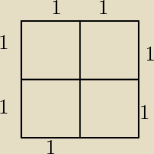
Narysujmy kwadrat o boku 2, następnie podzielmy go na cztery takie same kwadraty, zatem każdy z
tych kwadratów ma pole równe jeden bo 1*1=1 sumując wychodzi 4
30 lip 17:49
Saizou : to jak będzie z tym zadankiem
30 lip 18:20
rumpek: było
30 lip 18:22
rumpek: prostych zadań nie ma sensu dawać
30 lip 18:22
Saizou : to jak to udowodnić
30 lip 18:22
Saizou : to może trudniejsze, no ale bez przesadyzmu
30 lip 18:23
Eta:
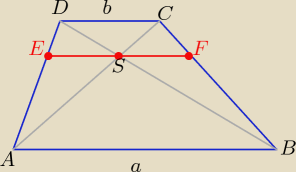
zad1/
Wykaż,że długość odcinka
EF jest równa średniej harmonicznej
długości podstaw trapezu.
30 lip 18:30
Saizou : eeee... co to jest średnia harmoniczna
30 lip 18:31
Eta:
Zapytaj "cioci Wiki"
30 lip 18:34
Mila: Jeśli nie wiesz, to oblicz EF i już będziesz wiedział. To jest zadanie z III klasy− program
rozszerzony.
Pozdrawiam Eta.
30 lip 18:36
Saizou : | | 2ab | |
inaczej mówiąc mam wykazać, że |
| =EF |
| | a+b | |
30 lip 18:47
Eta:
Dokładnie
30 lip 18:48
Saizou : jakaś mała podpowiedź
30 lip 19:05
rumpek: Podpowiedź: poszukaj tego w wyszukiwarce
30 lip 19:07
Saizou : bo dorysowałem sobie wysokości i jestem na:
30 lip 19:07
rumpek: podobienstwo trojkatow
30 lip 19:11
Eta:
Włącz myślenie
Patrz zad.5 ( z wczoraj )
30 lip 19:26
30 lip 19:29
rumpek: ja miałem taką
tyle, że w głowie
30 lip 19:30
Eta:
30 lip 19:31
Eta:
Nie każdy ma taką "wielką" ...........
30 lip 19:32
rumpek: miałem "ją"
dzięki rozwiązywaniu zadań na tym forum
30 lip 19:33
rumpek: 151854 tutaj takie na potem
30 lip 19:34
Saizou : EF=c
| (a+b)(h1*h2) | | ch2 | | ch2 | | bh2 | | ch1 | | ch1 | | ah1 | |
| = |
| + |
| + |
| + |
| + |
| + |
|
|
| 2 | | 2 | | 2 | | 2 | | 2 | | 2 | | 2 | |
z tego wynika że
(a+b)(h
1+h
2)=h
2(2c+b)+h
1(2c+a) i dalej nie wiem
30 lip 19:59
Eta:
Wczoraj wykazałeś,że |EF|= |ES|+|SF|= x+x
| | ah2 | | a | | h1 | |
|EF|=2x , x= |
| i |
| = |
| ⇒ h1=.... |
| | h1+h2 | | b | | h2 | |
|EF|= 2*x =......... dokończ.......
30 lip 20:09
30 lip 20:18
Eta:
I gitara
30 lip 20:21
Saizou : to co grasz
30 lip 20:22
rumpek: ja chętnie pogram
30 lip 20:23
Eta:
W brydża? .... chętnie
30 lip 20:24
Saizou : ja i muzyka to sprzeczność
30 lip 20:24
rumpek: szachy
30 lip 20:24
Saizou : to może od razu w szachy
30 lip 20:25
Saizou : zrobiłem Printscreen'a i mam w formie obrazka
, ustawię sobie na tapetę
30 lip 20:30
rumpek